4.2. Ориентированные, упорядоченные и бинарные деревья

Ориентированным деревом (ордеревом, корневым деревом) называется орграф со следующими свойствами.

1. Существует единственная вершина, полустепень захода которой равна 0. Она называется корнем ориентированного дерева.

2. Полустепень захода всех остальных вершин равна 1.

3. Каждая вершина достижима из корня.

Например:

а) все возможные ориентированные деревья с 3-я вершинами:

Р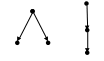 ис. 15

с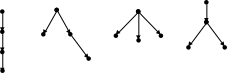 4-я вершинами:

Рис. 16

Концевая (висячая) вершина ордерева называется листом. Путь из корня в лист называется ветвью.

Уровень вершины ордерева – это расстояние от корня до вершины. Корень имеет уровень 0. Вершины одного уровня образуют ярус дерева.

Эквивалентное определение ориентированного дерева

Ордерево D – это конечное множество вершин, таких что:

1) имеется одна вершина r, называемая корнем данного дерева;

2) остальные вершины содержаться в k попарно непересекающихся множества D₁,…D_k , каждое из которых является ордеревом. (k0) D= .

Множества D₁,…,D_k называются поддеревьями.

Упорядоченным деревом называется ориентированное дерево, в котором:

1. задан порядок поддеревьев

2. каждое поддерево D_i является упорядоченным поддеревом.

3. дерево с одной вершиной считается упорядоченным поддеревом.

Замечание. При изображении ориентированных деревьев принято соглашение о том, что корень размещается вверху. В связи с этим все дуги оказываются ориентированными сверху вниз, поэтому стрелки на них можно не изображать. В результате, диаграммы свободных, ориентированных и упорядоченных деревьев оказываются графически неотличимыми. В этом случае требуется дополнительное указание, какого класса дерево изображено на диаграмме. Обычно это ясно из контекста.

Н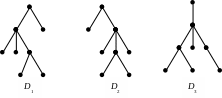 апример: Имеются 3 диаграммы деревьев:

Рис. 17

Как упорядоченные деревья, они все различны. Как ориентированные деревья D₁=D₂D₃. Как свободные деревья, они все изоморфны D₁=D₂=D₃.

Терема 3. Число упорядоченных деревьев с m дугами не превосходит 4^m.

Доказательство: Рассмотрим алгоритм обхода упорядоченного дерева, называемого «поиском в глубину». Этот обход рекурсивно описывается следующим образом:

1. Начать с корня. Пока есть деревья выполнять.

2. Перейти в корень очередного поддерева, обойти это поддерево в глубину.

3. Вернуться в корень исходного поддерева.

В результате «обхода в глубину» по каждой дуге проходят ровно 2 раза: один раз при переходе в очередное поддерево, второй раз – при возвращении из него. В соответствии с «обходом в глубину» строиться последовательность из нулей и единиц. На каждом шаге записывается нуль, если происходит переход в очередное поддерево, а единица – при возвращении из поддерева. В результате получается последовательность из нулей и единиц длины 2m, которая называется кодом дерева. По этому коду однозначно восстанавливается дерево, т.к. каждый очередной разряд однозначно указывает, начинать ли строить новое очередное поддерево или возвращаться на ярус

ближе к корню. Таким образом. упорядоченных деревьев с m дугами не больше, чем последовательностей из нулей и единиц длины 2m. А их число равно 2^2m=4^m. Теорема доказана.

Изоморфизм ориентированных деревьев определяется так же, как и изоморфизм графов, но с дополнительным условием - корень должен отображаться в корень. Для упорядоченных деревьев требуется также сохранение порядка поддеревьев.

Следствие. Число неизоморфных ориентированных или свободных деревьев с m ребрами не превосходит 4^m.

Доказательство: Выделив в неизоморфных свободных деревьях по одной вершине, мы получаем неизоморфные ориентированные деревья. Упорядочивая поддеревья в неизоморфных ориентированных поддеревьях, мы получаем упорядоченные деревья. Поэтому число неизоморфных свободных деревьев с m ребрами не превосходит числа неизоморфных ориентированных деревьев с m дугами, которое в свою очередь не превосходит числа неизоморфных (различных) упорядоченных деревьев с m дугами. Отсюда из теоремы 3 следует утверждение следствия.

Бинарное дерево – это конечное множество вершин, которое либо пусто, либо состоит из корня и не более двух непересекающихся бинарных поддеревьев – левого и правого. Заметим, что бинарное дерево не является упорядоченным.

Пример: два различных бинарных дерева:

Р ис. 18

Эти деревья изоморфны как упорядоченные, ориентированные и свободные, но не изоморфны как бинарные деревья.