11. Задача коммивояжера
11.1. Постановка задачи
Коммивояжер или торговый агент реализует товар в нескольких населенных пунктах, расположенных на определенных расстояниях друг от друга. Коммивояжер должен объехать все эти пункты по кратчайшему маршруту и вернуться обратно. С точки зрения теории графов задача коммивояжера формулируется как задача нахождения гамильтонова цикла минимальной длины.
Многие практические задачи сводятся к задаче коммивояжера. Например:
Пусть граф задает сеть коммуникаций между фиксированными центрами. Необходимо построить маршрут, обеспечивающий все центры проходя через них ровно по одному разу.
Имеется станок с числовым программным управлением (ЧПУ), который высверливает отверстия в печатных платах по заданной программе. Составляется граф, вершины которого соответствуют требуемым отверстиям. Необходимо найти такой обход вершин графа, чтобы суммарное время обхода было минимальным.
11.2. Обходы вершин графа по глубине и ширине
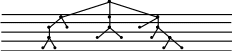
При решении прикладных задач часто возникает необходимость обхода вершин графа, связанная с поиском вершин, удовлетворяющих определенным свойствам. Пусть G(V, E) – связный граф, N – некоторый остов графа G, а – некоторая фиксированная вершина, называемая корнем дерева Т. Разместим вершины из V по этажам таким образом, чтобы корень а находился в верхнем этаже, а смежные с корнем вершины находятся на этаж ниже. Вершины, смежные с отмеченными вершинами находятся на этаже еще на единицу ниже и т.д.
r
1
2
3
4
5
Рис. 35
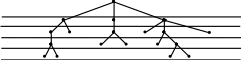
Рассмотрим обход графа по глубине.
При таком обходе после очередной рассмотренной вершины выбирается смежная с ней вершина следующего этапа. Если очередная рассмотренная вершина висячая и ее достижение не дает желаемого результата, то необходимо вернуться до ближайшей вершины и просмотреть в таком же порядке вершины другого , еще не пройденного, маршрута и т.д.
Например:
1
.
2 8 12
3 7 9 13 14 19 4 10 11 15 16
5 6 17 18
Рис. 36
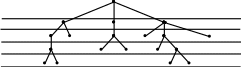
При обходе графа по ширине просмотр вершин дерева ведется по этажам. Переход к вершинам следующего этажа производиться только после просмотра всех вершин данного этажа.
Например:
1
2 3 4
5 6 7 8 9 10
11 12 13 14 15
16 17 18 19
Рис. 37
Заметим, что при обходе всех вершин оба подхода эквивалентны. Если же требуется найти одну вершину с определенными свойствами, то целесообразность применения обхода по глубине или ширине определяется структурой дерева. Если дерево достаточно широкое, то висячие вершины расположены на сравнительно близких этажах, поэтому в этом случае целесообразно вести поиск по глубине. Для глубоких и узких деревьев висячие вершины могут находиться на разных этажах, поэтому предпочтение в этом случае отдается поиску по ширине.
При компьютерной реализации обходов по глубине и ширине целесообразно использовать задание дерева структурой смежности вершин.
Часто при решении задач их разбивают на несколько более простых задач, которые в свою очередь разбивают на еще более простые подзадачи и так до тех пор, пока не появляются подзадачи, поддающиеся непосредственному решению. Такое разбиение задач можно представить в виде дерева. Если задача А разбивается на подзадачи А(1,1)А(1,2),…, А(1,n), подзадачи А(1, i) на подзадачи А(2,i,1), A(2,i,2),…, A(2,i,n2i) и т.д. получается следующее дерево.
А
А(1,1) А(1,n1)
А(1,2)…
А(2,1,n)
A(2,n1,n2n1) A(2,n1,1)…
A(2,1,n21)
A(2,2,n2)….
A(2,2,1)…
… … …
… … …
Рис. 38
Для решения поставленных задач используются обходы таких деревьев с поиском по глубине и по ширине. Рассмотрим данный подход на примере решения задачи Коммивояжера методом ветвей и границ.