10. Кратчайшие маршруты в графах

10.1. Расстояния в графах

Пусть G=(V, E) – связный неориентированный граф, u,v – две несовпадающие вершины. Длина кратчайшего (u, v) – маршрута называется расстоянием между вершинами u и v и обозначается (u, v).

Полагается, что (u, u)=0. Расстояние удовлетворяет аксиомам метрики:

1. (u, v)0

2. (u, v)=0 тогда и только тогда, когда u=v

3. (u, v)= (v, u) (свойство симметричности)

4. (u, v) (u, t)+ (t, v) (неравенство треугольника)

Матрица P=p_i,j , где p_i,j =(v_i, v_j), называется матрицей расстояний. Заметим, что матрица расстояний симметрична (P^T=P).

Величина E(v)=max{(u,v)|uV} называется эксцентриситетом вершины v. Эксцентриситет вершины равен расстоянию от данной точки до наиболее удаленной от нее.

Эксцентриситет e(v­_j) равен наибольшему из чисел стоящему в j-ой строке матрицы расстояний.

Максимальный среди всех эксцентриситетов вершин называется диаметром графа G и обозначается D(G). D(G)=max e(v_j)

Вершина v называется периферийной, если ее эксцентриситет e(v)=D(G).

Минимальный из эксцентриситетов графа G называется его радиусом и обозначается R(G). R(G)=min{e(v)|vV}

Вершина v графа G называется центральной, если e(v)=R(G).

Множество всех центральных вершин графа называются его центром.

П ример: Рассмотрим граф 4 5

2

1 3

Рис. 33

Матрица расстояний: P=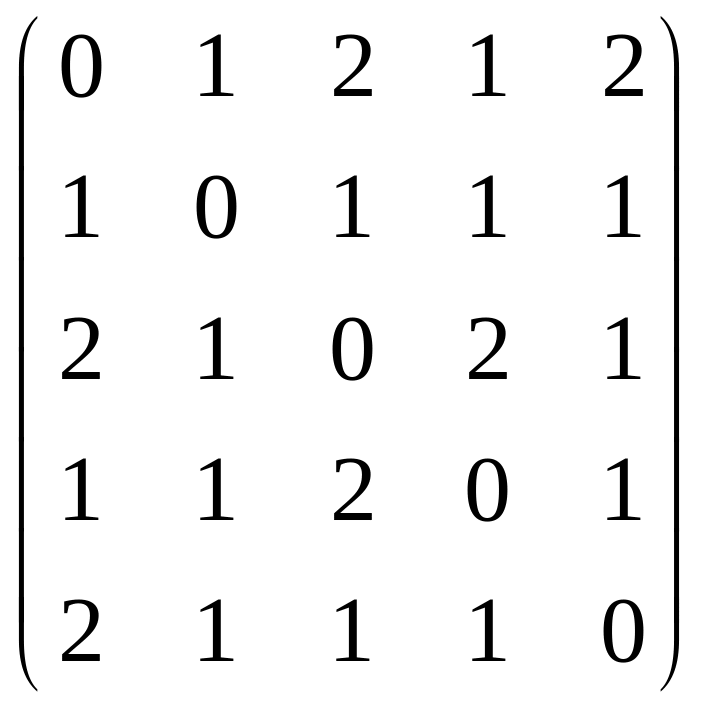

Отсюда e(1)=2; e(2)=1; e(3)=2 e(4)=2; e(5)=2, следовательно, D(G)=2 , а вершины {1, 3, 4, 5} являются периферийными. R(G)=1. Центр графа - {2}.

В полном графе D(K_n)=R(K_n)=1

Задача нахождения центральных вершин возникает в практической деятельности людей. Например, пусть в графе вершины соответствуют населенным пунктам, а ребра - дорогам между ними. Требуется оптимально разместить больницы, пункты обслуживания и другие объекты. Местами их размещения должны быть центральные вершины графа. Реальные задачи отличаются от идеальных тем, что приходиться учитывать расстояния между населенными пунктами, время проезда, стоимость и т.д. Для учетов этих параметров используются взвешенные графы.

Пусть G=(V, E) – взвешенный граф, в котором вес каждой дуги (u,v) есть некоторое вещественное число (u,v).

Весом маршрута v₁, v₂, …, v_n, v_n+1 называется число = .

Взвешенным расстоянием ( расстояние) _(u,v) между вершинами u и v называется минимальный из весов (u,v) – маршрутов.

(u,v) – маршрут, вес которого равен _(u,v) называется кратчайшим (u,v) маршрутом графа G.

Взвешенным эксцентриситетом e_(v) вершины v называются числа max{_(u,v)|uV}.

Взвешенной центральной вершиной графа G называется вершина v, для которой e_(v)=min{ e_(u)|uV}.

Взвешенный эксцентриситет центральной вершины называется взвешенным радиусом графа G, и обозначается как R_(G).

10.2. Алгоритм Форда-Беллмана

Пусть G=(V, E) – взвешенный граф, имеющий n вершин и матрицу весов W=(_ij). Требуется найти взвешенное расстояние от фиксированной вершины v_iV называемой источником, до всех вершин графа G.

Предполагается, что в G отсутствуют контуры с отрицательным весом т.к. двигаясь по такому контуру достаточное число раз можно получить маршрут меньший любого, наперед заданного, числа. В этом случае задача нахождения расстояния становиться бессмысленной.

Алгоритм Форда-Беллмана заключается в том, что задается строка Д⁽¹⁾=(d⁽¹⁾₁, d⁽¹⁾₂, d⁽¹⁾₃, …, d⁽¹⁾_n), в которой d⁽¹⁾_i=0, d⁽¹⁾_j=_ij, если ij.

Предполагается, что все дуги _ij=, если (v_i, v_j)E

Далее определяется строка Д⁽²⁾=(d⁽²⁾₁, d⁽²⁾₂, d⁽²⁾₃, …, d⁽²⁾_n), где d⁽²⁾_j=min{d⁽¹⁾_j, d⁽¹⁾_k+_kj}

Заметим, что d⁽²⁾_j – минимальный из весов (v_i, v_j) маршрутов состоящих не более чем из двух дуг.

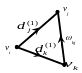
Рис. 34

П родолжая этот процесс на шаге s определяется строка Д⁽³⁾=(d⁽³⁾₁, d⁽³⁾₂, d⁽³⁾₃, …, d⁽³⁾_n), в которой d⁽³⁾_j=min{d^(3-1)_j, d^(3-1)_k+_kj}, k=1,2,…,n

Искомая строка  - расстояний получается при s=n-1, т.е. d^(n-1)_j=(v_i v_j).

Действительно, на этом шаге из весов всех (v_i, v_j) маршрутов выбирается наименьший, а каждый маршрут с более чем n-1 дугами содержит контур, добавление которого к маршруту не уменьшает  - расстояния т.к. по условию в графе отсутствуют контуры отрицательного веса.

Работу алгоритма можно завершить на k-ом шаге (k<n-1), если Д^(к)=Д^(к+1).