14. Анализ технических систем (на примере электрической цепи)

14.1 Закон Кирхгофа

В данной теме рассматривается поведение технических систем. Исходной информацией для анализа любой системы является:

1) поведение ее составных частей и элементов

2) способы связи между ними

Метод, который здесь изложен, используется для анализа электрических цепей. Однако его можно применить к любым другим системам.

Имеется набор из m двухполосных элементов E₁,…,E_m. Двухполюсники соединены в n узлах P₁,…,P_n. Каждый элемент системы E_i характеризуется уравнением, связывающим ток x_i и напряжение y_j.

Пассивные элементы, не являющимися источниками энергии, характеризуются уравнениями :

y_i=kx_i – сопротивлением

y_i=k x_i – индуктивность

y_i=k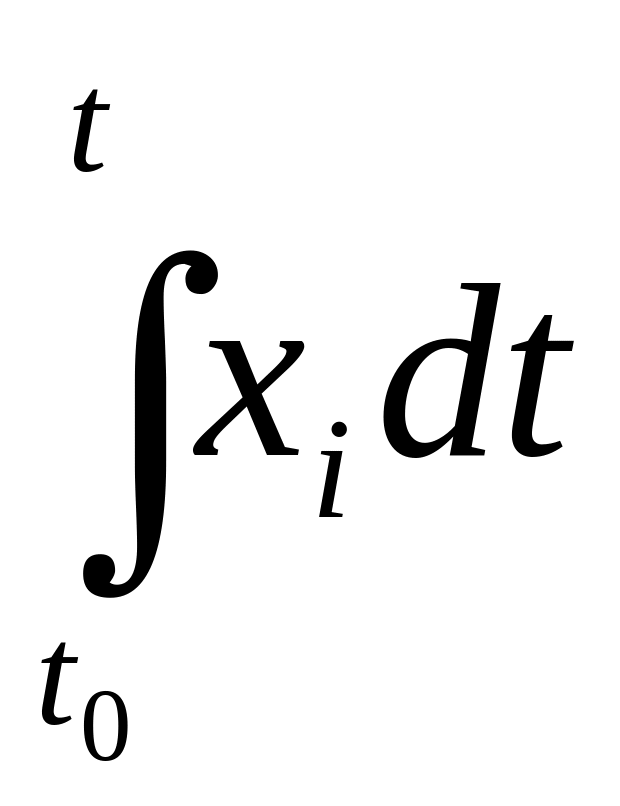 - емкость, где t – время.

Активные элементы (источники энергии) характеризуются уравнениями:

x_i=f(t) – источник тока

y_i=g(t) – источник напряжения

В простейшем случае f и g константы. Каждому элементу E_i соответствует дуга a_i, а каждому узлу P_j – вершина V_j. Полученный ориентированный граф называется топологическим (структурным) графом реальной технической системы.

В каждой вершине поведение токов подчиняется правилу вершин (1-ый закон Кирхгофа для тока).

Алгебраическая сумма токов, соответствующих дугам, инцидентны любой вершине, равны нулю.

В случае не электрических систем в качестве одной из базисных переменных тока следует выбирать такую переменную, для которой обеспечивается выполнение условий вершинного постулата.

Циклическое правило (2-ой закон Кирхгофа для напряжений): алгебраическая сумма напряжений, соответствующих дугам любого цикла равна нулю.

Предполагается, что циклу задается некоторая ориентация и каждое напряжение добавляется или вычитается, в зависимости от того, совпадает или не совпадает напряжение соответствующей дуги с выбранной ориентацией цикла.

Циклическое правило может быть переформулировано следующим образом. Если V₁ – фиксированная вершина, а V_i – любая другая вершина, отличная от V₁, то алгебраическая сумма напряжений по любой цепи, ориентированной от V₁ к V_i не зависит от выбранной цепи. Так как граф связен, то существует по крайней мере одна такая цепь. В результате для каждой вершины V_j можно определить число S_j=S₁-K, где K – алгебраическая сумма напряжений по любой цепи, направленной от V₁ к V_j , а значение S₁ – произвольно. В качестве V₁ можно выбрать любую вершину.

Таким образом, величины напряжений будут соответствовать разностям потенциалов.

14.2. Основные уравнения

Процесс получения уравнений, характеризующих состояние системы в целом, на основе уравнений ее элементов и заданной структуры проводиться в два этапа.

Сначала с помощью вершинного и циклического правил уменьшается количество переменных, соответствующих токам и напряжениям. В результате выделяется множество переменных, через которые можно выразить все переменные системы. Затем выписывается уравнение связи переменных тока и напряжения.

Рассмотрим первый этап процесса. Применяя к вершине V_i правило вершин, получим: , где

т.е. векторы A_i=(a_i1,a_i2,…,a_im) и X`=(x₁,…,x_m) являются ортогональными.

Здесь A_i есть строки матрицы A инциденций графа. Так как пространство натянутое на строке A совпадает с пространством, натянутым на строки матрицы разрезов K, X` есть линейная комбинация векторов циклов (строк матрицы циклов С). Таким образом, A (или K) и C определяют ортогональные подпространства, которые вместе образуют подпространство размерности m.

Используя материалы темы 6 K и C можно записать в виде K=(K₁|I) C=(I|C₂), где I – единичная матрица.

При выборе хорд стягивающего дерева в качестве первых m-n+1 столбцов. Разбивая таким же образом вектор токовых переменных, получим: X=( ) где X_c и X_b относятся к хордам и ветвям дерева.

Правило вершин означает, что KX(K₁|I)( )=0 следовательно

X_b= – K₁X_c=C^T₂X_c, т.е. (X=C^TX_c) (1)

Таким образом, токи в ветвях выражаются через токи в хордах.

Аналогично, циклическое правило приводит к матричным

уравнениям CY=(±|C)( )=0 Y_c=-C­­₂Y_b=K^T₁Y_b (Y=K^TY_b) (2)

Это уравнение выражает напряжение на хордах через напряжение на ветвях. Применение соотношений (1) и (2) составляет первый этап анализа.

Основные уравнения элементов удобно записать в матричной форме. Если напряжения заданны в виде явных функций от токов, то при этом получаем Y=Ω_xX-Y_g где Ω_x- диагональная m×m матрица, i – диагональный элемент который является либо константой, либо дифференциальным или интегральным оператором; Y_g – вектор столбец, элементы которого равны нулю, для позиций, соответствующих пассивным элементам и функциям g(t) для позиций, соответствующим источникам. Заметим, что соответствующие диагональные элементы Ω_x равны нулю.

Если токи выражаются как явные функции напряжения, то получим

X= Ω_yY-X_g (*)

Предыдущее выражение, с учетом (1), может быть переписано в виде :

Ω_xС^TX_c=Y+Y_g

Умножение обеих частей уравнения на C дает

C Ω_xC^TX_c=CY+CY_g=CY_g (3)

В этом выражении неизвестными являются лишь токи в хордах.

Выражение (*) может быть переписано

Ω_yK^TY_b=X+X_g

и затем

K Ω_yK^TY_b=KX+KX_g=KX_g (4)

где неизвестными являются только напряжения в ветвях.

Уравнения (3) и (4) соответствуют формулировкам задачи для циклов и вершин (узлов) соответственно. В случае, когда полученная система уравнений может быть решена известными математическими методами, оставшиеся неизвестными токи и напряжения легко находятся с приведенных выше соотношений.

В частности заметим, что K^T и C^T могут быть получены при визуальном анализе графа, после выбора дерева.

В случае, если некоторые элементы системы имеют более двух полюсов или если рассматриваются элементы согласования различных видов энергии в одной и той же системе, то матрица характеризующая основные уравнения, имеет более сложную структуру и решение результирующей системы уравнений получается более сложным. Тем не менее, роль графа, представляющего систему, остается по существу той же самой.