11.3. Решение задачи коммивояжера

Пусть W=(_ij) – матрица весов графа G(V,E), не имеющего петель. V={1,2,…,n}. Для простоты считается, что вес всех _ij неотрицателен. Предполагается, что _ij=, если i=j. Производиться нижняя оценка весов гамильтоновых циклов. Для этого в матрице весов находятся минимальные числа каждой строки: _1k1, _2k2, …,_nkn. Вес произвольного гамильтонова цикла не меньше _1k1+ _2k2+ …+ _nkn. Матрица преобразуется путем вычитания из каждой i-ой строки соответствующего числа _iki. В результате получается матрица W^v=(^v_ij), где ^v_ij=_ij - _iki. В полученной матрице ищутся минимальные числа в каждом столбце ^v₁₁, ^v₂₂, …,^v_inn. Матрица преобразуется вычитая из каждого j-го столбца соответствующее i-ое число ^v_ijj. В результате получается матрица W^*=(^*_ij), где ^*_ij=^v_ij-^v_ijj. Для любого гамильтонова цикла X справедлива оценка его веса

Далее вводиться обозначение (а₁, а₂, …,а_к) {b₁,b₂,…,b_t} – это множество гамильтоновых циклов, в которых первые k вершин

(X): (X)  h, где h=_1k1+_2k2+…+_nkn+^v_i11+^v_i22+…+^v_inn.

а₁, а₂, …,а_к а k+1 вершины а_k+1 не принадлежат множеству

{b₁,b₂,…,b_t}.

Используя введенное обозначение, разбиваем задачу на две подзадачи, путем разбиения всего множества гамильтоновых циклов на два множества (1, K₁) и (1){K₁} т.е. множества гамильтоновых циклов, содержащих

1. вершину 1 и K₁

2. вершину 1 и не содержащих K₁.

Каждая из этих подзадач делиться дальше и т.д. В результате дерево имеет сведущий вид:

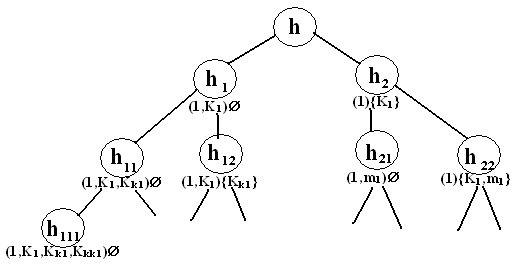
Рис. 39

При рассмотрении множества (1,K₁) отождествим в графе G вершин 1 и K₁ и обозначим новую образовавшуюся вершину через x. В результате получается граф G` с множеством вершин {x₁,2,…,k₁-1,k₁+1,…,n}.

Матрица весов имеет следующий вид:

W`=

Для графа G` найдем нижнюю оценку h` весов гамильтоновых циклов аналогично тому, как найдены оценки h. Тогда нижняя оценка h₁ весов гамильтоновых циклов множества (1,K₁) равна h+h`.

При рассмотрении множества (1){K₁} в матрице весов W* элемент заменяется на  и по полученной матрице W``` находится нижняя оценка h`` весов гамильтоновых циклов множества (1){K<sub>1</sub>} равна h+h``.

Каждая из подзадач разбивается на свои подзадачи, и этот процесс с оцениванием весов гамильтоновых циклов продолжается до тех пор пока не отыщется самая низкая из оценок являющаяся весом некоторого гамильтонова цикла, который и будет иметь минимальный вес.

При рассмотрении подзадач целесообразно вести поиск в глубину, при котором на каждом следующем этаже выбирается та подзадача, которая имеет меньшую нижнюю оценку.

12. Потоки в сетях

12.1. Основные определения

Если в графе ориентировать все ребра, то получится орграф, который называется направленным. Направленный орграф, полученный из полного графа, называется турниром.

Если в орграфе полустепень захода некоторой вершины равна нулю, т.е. d⁺(V)=0, то такая вершина называется источником, если же нулю равна полустепень исхода, т.е. d^-(V)=0, то вершина называется стоком. Направленный орграф без петель с одним источником и одним стоком называется (двухполюсной) сетью.

Пусть G (V, E) – сеть, а S и t – соответственно источник и сток сети. На множестве дуг сети определена неотрицательная функция C: ER⁺, ставящая каждой дуге (U,V) неотрицательное вещественное число C(U, V), называемое пропускной способностью дуги (U, V).

Пусть заданна функция f: ER. Дивергенцией функции f в вершине V называется число div(f,V), которое определяется следующим образом: div(f,V)= -

Функция f: ER называется потоком в сети G, если:

1)  (U,V)E 0f(U,V)C(U,V)

2)  VV\{s,t} div(f,V)=0

Число (f)=div(f,s) называется величиной потока f.

Замечание. Первое условие в определении потока означает, что поток через дугу неотрицателен и не превосходит пропускной способности дуги. Второе условие означает, что количество потока, входящего в каждую вершину сети (кроме истока и стока), равно количеству потока, выходящего из этой вершины.

С помощью потоков в сети можно моделировать:

1) автомобильные потоки на дорогах

2) перекачку нефти на нефтепроводе

3) последовательность технологических операций для производства готовых изделий из сырья.

4) передачу информации в компьютерной сети

В данной лекции рассматривается решение только одной (но самой существенной) задачи этой теории – нахождения максимального потока в сети.

Для решения этой задачи сеть разбивается на два непересекающихся множества таким образом, чтобы исток попал в одно множество, а сток – в другое. В этом случае говорят, что на сети произведен разрез, отделяющий исток от стока.

Пусть P – (s,t) разрез, PE. Всякий разрез определяется разбиением множества вершин V на два подмножества A и B так, что A,BV, AB=V, AB=0, sA, tB. Разрез обозначается P(A) и представляет собой множество дуг (U,V)E, таких, что UA, VB.

Пропускной способностью разреза называется сумма пропускных способностей входящих в него дуг C\A=

Минимальным разрезом, разделяющим исток s и сток t сети, называется произвольный разрез P(A) sA, tV\A с минимальной пропускной способностью.