7. Связь теории графов с бинарными отношениями и векторными пространствами

7.1. Отношения на множествах и графы

Любой ориентированный граф G=(V, E) с петлями, но без кратных дуг, задаёт бинарное отношение E на множестве V своих вершин, и обратно Пара элементов (a, b) принадлежит отношению EVV тогда и только тогда, когда в графе G имеется дуга (a, b). Таким образом, имеется полная аналогия между бинарными отношениями и орграфами. Рассмотрим различные виды отношений с точки зрения теории графов.

Нулевое отношение соответствует ноль-графу. Полный граф взаимнооднозначно соответствует универсальному отношению. Дополнение графов есть дополнение отношений. Изменение направления всех дуг соответствует обратному отношению.

Отношению со свойствами рефлексивности aRa на графе должна соответствовать петля в некоторой вершине a. Если отношение рефлексивности соблюдается для всех элементов, то соответствующий граф имеет петли во всех вершинах. В случае антирефлексивного отношения соответствующий граф не имеет петель ни в одной из вершин.

Симметричному отношению на множестве V соответствует граф с неориентированными ребрами. В свою очередь граф с ребрами определяет некоторое симметричное отношение. В случае антисимметричного отношения в графе невозможно присутствие одновременно двух дуг (v_i, v_j) и (v_j, v_i), т.е. в графе могут быть только дуги, но не должно быть ребер.

Граф соответствующий транзитивному отношению, обладает тем свойством, что для каждой пары дуг (v_i, v_j) и (v_j, v_k) имеется замыкающая их дуга (v_i, v_k), то есть, так как показано ниже на рисунке.

Р ис. 25

В графе, соответствующем транзитивному отношению, для

к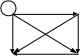 аждого пути S(v_i, v_k) существует дуга его замыкающая (v_i, v_k). Граф соответствующий транзитивному отношению:

Рис. 26

Г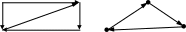 рафы нетранзитивные:

Рис. 27

Р ассмотрим графы, соответствующие отношению эквивалентности (рефлексивность, симметричность и транзитивность). Такие графы представляют собой совокупность компонент связности, причем для каждого класса эквивалентности своя компонента связности. Каждая компонента связности должна быть полным неориентированным графом с петлями. Пример графа, с отношением эквивалентности.

Рис. 28

При рассмотрении отношения нестрого порядка (рефлексивность, антисимметричность и транзитивность) соответствующий граф должен иметь петли в каждой вершине и слдержать только дуги. В силу транзитивности в графе для каждого пути S(v_i,v_k) должна существовать дуга, его замыкающая -(v_i, v_k).

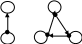Примеры:

Рис. 29

Граф, на множестве вершин которого определено отношение строго порядка (антирефлексивным, антисимметричным и транзитивным), получается удалением всех петель в графе, на множестве вершин которого определено отношение нестрогого порядка.

Справедливы следующие утверждения:

1. Если отношение является строго упорядоченным, то соответствующий упорядоченный граф не имеет контуров.

2. Если орграф не имеет контуров, то достижимость является строго упорядоченной.

3. Если орграф не имеет контуров, то в нем есть вершина, полустепень захода которой равна 0.

Замечание. Последнее утверждение позволяет определить минимальный элемент в конечном частично упорядоченном множестве. А именно, минимальный элемент – это есть источник, т.е. вершина, которой в матрице смежности соответствует нулевой столбец.