8. Планарность и раскраска графов

8.1. Планарные графы

При изображении графа имеется полная свобода при размещении вершин и выборе формы соединяющих их ребер. Геометрическим графом называется множество точек в n-мерном евклидовом пространстве, взаимосвязанных между собой набором непрерывных самонепересекающихся кривых.

Теорема 1. В трехмерном пространстве любой конечный граф можно представить так, что линии, соответствующие ребрам (дугам) не пересекаются во внутренних точках.

Доказательство. Пусть граф G=(V,E) содержит n вершин и m рёбер. Возьмём прямую в трёхмерном пространстве и проведём через неё m различных плоскостей. На прямой выделим точки , которые будут соответствовать вершинам графа . Каждое ребро графа G будет соответствовать одной из проведённых плоскостей. Пусть - ребро графа G. В плоскости, соответствующей ребру e, соединим точки a_i и a_j дугой окружности. Выполнив такое построение для всех рёбер графа G, поучим из точек и дуг окружностей требуемую геометрическую реализацию графа G. Теорема доказана.

У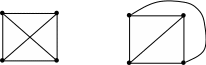 кладкой графа на некоторой поверхности называется такое его изображение на этой поверхности, при котором никакие два ребра не будут иметь общих точек, кроме быть может, общего конца этих ребер. Плоский граф – это граф, уложенный на плоскости. Граф называется планарным, если его можно уложить на плоскости. Например, граф, изображённый

Рис. 30

Область, ограниченная ребрами (дугами) в плоском графе, и не содержащая внутри себя вершин и ребер называется гранью.

Число граней плоского графа обозначается r(G). При этом считается, что внешняя часть плоскости графа также образует грань. Например, вышеприведенный граф К₄ (полный граф с 4-я вершинами) имеет 4-е грани.

Для графов, уложенных на некоторой поверхности справедливо определенное соотношение между числом вершин, ребер и граней. Это соотношение называется эйлеровой характеристикой поверхности.

Теорема 2 (Формула Эйлера). В связном планарном графе справедливо соотношение , где n – число вершин, m – число ребер, r –число граней.

Доказательство. Проводится по индукции числа m. Во-первых, при m=0, имеем n=1 и r=1, то есть, теорема справедлива. Во-вторых, положим, что теорема верна для всех графов с m рёбрами, то есть справедливо выражение n-m+r=2. В третьих, добавим к графу ещё одно ребро. Если добавляемое ребро соединяет существующие вершины, то число рёбер в новом графе , число вершин - и число граней - . Следовательно, . Если добавляемое ребро соединяет существующую вершину с новой вершиной, то имеем и следовательно . Таким образом, теорема доказана.

Следствие 1. Если G – связный планарный граф, у которого n>3, то m3n-6.

Доказательство. Обозначим через m_i – число рёбер в i-ой грани. Каждая грань плоского графа ограничена, по крайней мере, тремя рёбрами, то есть .Суммируя по всем граням и учитывая то, что каждое ребро входит в две грани, получим: или . В соответствии с эйлеровой характеристикой плоскости имеем:

.

Что и требовалось доказать. Прежде чем приступать к формулировке следующего следствия, необходимо ознакомиться с рядом определений.

Неориентированный граф G называется двудольным, если множество всех ребер графа образует разрез графа, т.е. для некоторого разбиения вершин {V₁, V₂}, концы любого ребра принадлежат разным частям разбиения.

Если двудольный граф содержит все рёбра соединяющие множества V₁ с V₂, то он называется полным двудольным графом.

Если |V₁|=m, а |V₂|=n, то полный двудольный граф обозначается K_m,n.

Например, граф K_3,3 имеет следующий вид:

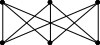
Рис. 31

Следствие 2. Графы К₅ и К_3,3 непланарны.

Д о к а з а т е л ь с т в о: (от противного) Предположим, что граф К₅ – планарен, тогда по первому следствию – получили противоречие, следовательно, граф К₅ не является планарным.

Пусть далее К_3,3 – планарен. Для него имеем n=6, m=9. В этом графе нет треугольников, а так как. граф планарен, то при его плоской укладке каждая грань ограничена не менее, чем 4 ребрами. Из этого следует, что , а значит 2rm. В соответствии с эйлеровой характеристикой плоскости имеем: 6-9+r=2, следовательно r=5. Таким образом: - противоречие, а это значит, что К_3,3 непланарен.

Теорема Понтрягина-Куратовского (критерий планарности).

Граф G планарен тогда и только тогда, когда G не содержит подграфа гомоморфного К₅ или К_3,3. Эквивалентная формулировка этой теоремы: неориентированный граф G планарен тогда и только тогда, когда G не содержит подграфов, стягиваемых (т.е. получаемых последовательностью отождествлений вершин, связанный ребрами) к графу К₅ или К_3,3.

Если граф непланарен, то для его плоской реализации удаляют отдельные рёбра, перенося их на другую плоскость. Минимальное число ребер, которое необходимо удалить из графа для получения его плоского изображения называется числом планарности графа G.

При вынесении этих ребер на вторую плоскость, получается часть графа, которая также может оказаться неплоской. Тогда вновь возникает задача вынесения отдельных ребер на следующую плоскость и т.д.

Минимальное число плоскостей, при которых граф G разбивается на плоские части G₁, G₂, …, G_m (разбиение производиться по множеству ребер) называется толщиной графа G.

Например, толщина планарного графа равна 1, а графы К₅ и К_3,3 имеют толщину равную 2.