Методическое пособие 733

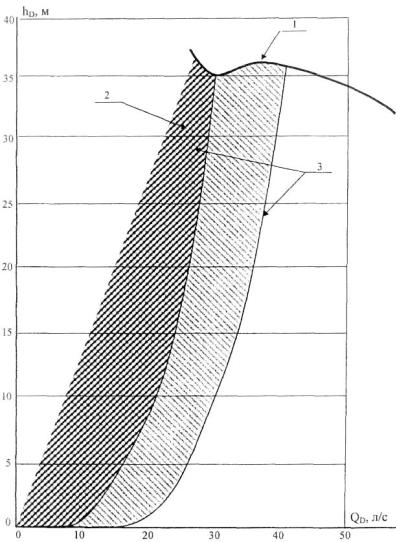
Рис. 2.6. Иллюстрация результатов моделирования дроссельных характеристик в области прямого анализа системы водоснабжения (рис. 2.3)

для участков с дросселями (12-29) и (16-24):

1 – дроссельная характеристика для области обратного анализа для участков с дросселями (12-29) и (16-24); 2 – дроссельная характеристика для области прямого анализа для участка с дросселем (12-29); 3 – дроссельная характеристика для области прямого анализа для участка с дросселем (16-24)

Вдальнейшем изложении рассматривается альтернативный подход к формализации дроссельных характеристик, но не на базе крайне неудобной прямой задачи, а на основе обратной задачи анализа возмущенного состояния РСВ, которая исходит из априорно заданного режима водопотребления. С этой целью проанализируем возможности векторно-информационного пространства

вобласти управления гидравлическими трубопроводными системами [45].

Вдальнейшем изложении рассматривается альтернативный подход к формализации дроссельных характеристик, но не на базе крайне неудобной прямой задачи, а на основе обратной задачи анализа возмущенного состояния РСВ, которая исходит из априорно заданного режима водопотребления. С этой целью проанализируем возможности векторно-информационного пространства

вобласти управления гидравлическими трубопроводными системами [45].

81

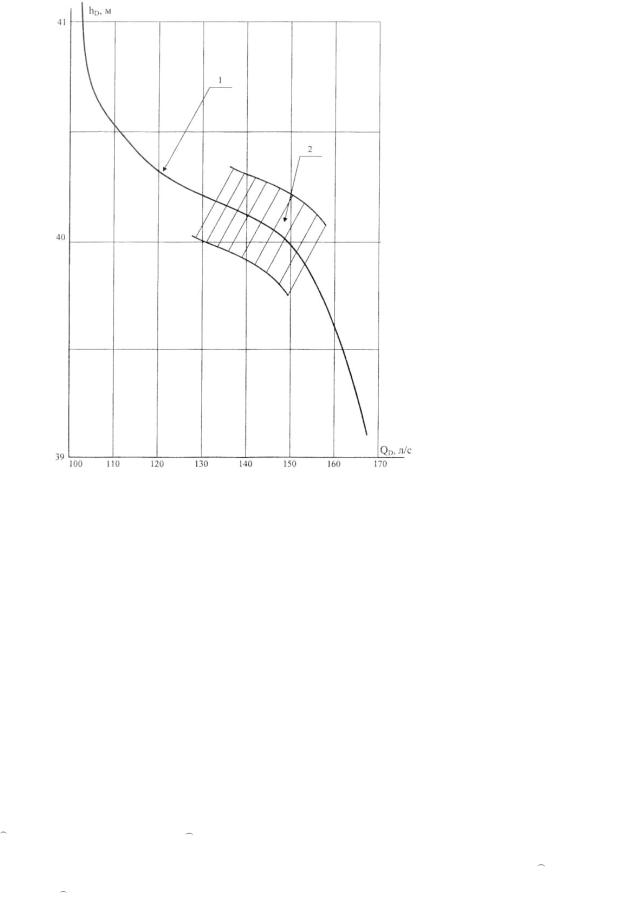
Рис. 2.7. Дисперсия дроссельной характеристики участка (14-22), синтезируемой в области прямого анализа водоснабжающей системы (рис. 2.3):

1 – дроссельная характеристика для области обратного анализа;

2 – дроссельная характеристика для области прямого анализа

Модель потокораспределения любого (возмущенного или невозмущенного) состояния U(Z) = U(Y,X) = 0 гидравлической трубопроводной системы на установившемся режиме потребления ЦП, например [2, 54, 71, 72 и др.] позволяет однозначно определять искомый вектор параметров состояния Z, включающий векторы зависимых Y и независимых X переменных, при условииik 0 , известном как правило Крамера (где ik – элемент матрицы

коэффициентов системы неоднородных линейных уравнений [37]).

В состав вектора Y традиционно включаются векторы расходов среды Q с компонентами Qi ( i I – множество участков системы); вектор полных пьезометрических напоров Н с компонентами H j ( j J JH ( где J – полное

множество узлов системы).

Всостав вектора X включаются: векторы D, L с компонентами Di, Li, i I

,вектор H , с компонентами H j ( j JH – полное множество ЭУ-стоков с

фиксированным узловым потенциалом); вектор узловых отборов (притоков) q , с компонентами q j ( j Jq – полное число ЭУ с фиксированным узловым

82

отбором (притоком), включая и нулевой отбор, причем JH Jq JZ –

полное число ЭУ. Компоненты вектора X включаются в состав условий однозначности. Это традиционная постановка задачи моделирования потокораспределения в рамках прямого анализа.

В отличие от постановки задачи прямого анализа в данном случае предлагается осуществить перевод определяющего вектора SD из множества независимых в состав зависимых переменных с сохранением за ним функций возмущающего параметра. При этом механизм взаимосвязи потокораспределения с параметрическим характером возмущения не меняется и сохраняется в рамках топологической модели (1.31) – (1.33).

Моделирование процессов управления РСВ, реализуемых целенаправленным воздействием на множество ID дросселей, должно базироваться на прогнозе потребления воды. Структурообразующей основой векторно-информационного пространства при формализации в подобной постановке процессов управления является, как и в прямой задаче анализа, модель возмущенного состояния, отображаемая в условиях любых форм возмущения бинарным структурным графом. С целью упрощения выкладок рассматривается частный случай эквивалентирования метасистемы (АП) множеством тупиковых ответвлений от ЭУ расчетной зоны, известный как "тупиковый принцип эквивалентирования".

В зависимости от включения множества SDi в состав векторов X или Y матрица (1.31) – (1.33) может быть квадратной или прямоугольной конфигурации. В первом случае SDi должны быть заданы в задачах прямого анализа, во втором – они подлежат определению, что характерно для области обратного анализа.

Несомненный интерес представляет синтез дроссельных характеристик РСВ в области обратного анализа, с заманчивой перспективой точного прогноза глубоких изменений режима потребления. Однако задача обратного анализа строится на основе прямоугольной матрицы возмущенного состояния с неизвестными компонентами SDi , j ID и ставит своей целью определение

последних (помимо расчета потокораспределения) при априорно заданном режиме потребления воды. Подобная постановка вынуждает искать дополнительные линейно независимые связи, избыточные по отношению к связям, синтезирующим структуру МВС (1.31) – (1.33). Отметим, что модель возмущенного состояния получена как результат решения вариационной задачи, отражающей принцип наименьшего действия применительно к гидравлическим трубопроводным системам, то есть связь между векторами Y и X формируется на уровне функционала, и в этом смысле себя исчерпала. Дополнительные связи следует искать на основе других (не энергетических, а вероятностных) принципов, например в недрах регрессионного анализа, и такая связь устанавливается с помощью метода наименьших квадратов (МНК) [45].

83

2.4. Формирование модели управления системами водоснабжения на основе оптимизационного механизма обратной связи

Проведение вычислительных экспериментов в области гидромеханики сетей, как, впрочем, и в любом другом научном направлении, основывается на применении математического моделирования, которое приобрело в последнее время широкий размах благодаря бурному прогрессу вычислительной техники, преимущественно индивидуального пользования (ПЭВМ), обеспечившему широкий доступ к электронным вычислительным средствам массового пользователя. Методология математического моделирования и последующего вычислительного эксперимента содержит ряд последовательно протекающих этапов, основными из которых являются: а) инженерная (содержательная) постановка задачи с определением целей исследования; б) формализация и формирование математической модели на основе известных фундаментальных законов сохранения основных физических величин (энергии, количества движения, массы и др.); в) разработка алгоритма и компьютерной программы его реализации; г) проведение вычислительною эксперимента; д) анализ результатов моделирования и проверка адекватности модели с ее корректировкой в случае необходимости.

Для формирования целевой функции предлагается использовать суррогатный (не основанный на физических законах) принцип ЛежандраГаусса, получившего известность как метод наименьших квадратов (МНК). Квадратичный функционал, составленный на основе МНК, представляет из себя некую остаточную функцию F, в данном случае для множества компонентов векторов H и Q, связанных между собою зависимостью в форме уравнения Бернулли. Решение задачи сводится к минимизации функционала F. Однако неизвестной в структуре функционала является весовая функция ω, зависящая от среднеквадратической погрешности измерения параметра и отображающая степень доверия к системе измерений.

Поскольку данная задача не связана с измерениями, а дисперсия соответствующего параметра определяется точностью вычислительных средств, можно допустить, что весовая функция является для всех узловых параметров величиной одинаковой. В этом случае она не влияет на положение минимума функционала.

Впервые использование в основе целевой функции уравнения Бернулли рассмотрено и изучено в работе [45] применительно к распределительным системам газоснабжения среднего давления. Основным недостатком этой версии целевой функции является высокая степень нелинейности, которая приводила к определенным вычислительным проблемам. Число итераций в вычислительном эксперименте достигало К = 100×103, что повлекло необходимость наращивания ресурсов ПЭВМ.Рассмотрим эту версию целевой функции применительно к системам водоснабжения [55, 57].

Поскольку решение ищется для области управления, целевая функция F должна отражать режим потребления воды от энергоузлов РЗ, то есть уравнение Бернулли должно быть записано для двух сечений, пересекающих

84

узлы, инцидентные фиктивным участкам, которые и определяют означенный режим.

Запишем эти уравнения для одного из фиктивных участков РСВ (рис. 2.1) с расположением дроссельных элементов на ответвлениях к ЭУ выделенного расчетного фрагмента. Как отмечалось выше, такая схема БСТГ позволяет достаточно полно контролировать режим потребления:

Учитывая равномерное движение среды в трубопроводе, можно пренебречь изменением скорости потока между контрольными сечениями и переписать уравнение (2.17) для граничных условий МВС

(H11=H12=H13=H14=H15 = 0):

Согласно традиционной постановке задачи МНК функцию (2.18) следует записать для двух сопоставимых версий по расходу на фиктивном участке: первая компьютерная версия строится по результатам моделирования возмущенного состояния РСВ, вторая – версия пользователя в части, касающейся режима потребления, поскольку для пользователя, обладающего соответствующим опытом проектирования и эксплуатации водоснабжающих систем, именно режим потребления воды от каждого энергоузла является наиболее доступной и значимой информацией. Пользователь, не владеющий обратной связью между режимом потребления и гидравлической настройкой дросселей больших систем сложной конфигурации, может воспользоваться МНК для установления этой связи. С этой целью запишем для версии (2.18) применительно к схеме на рис.2.1:

компьютерной версии и версии пользователя ( Qfz – априорно заданный пользователем расход через фиктивный участок, присоединенный к энергоузлу

2, РФ).

Используя форму записи (2.19), представим целевую функцию применительно к РCВ (рис. 2.1, mH = 5), составленную на основе МНК (где mH

– число узлов-стоков с фиксированным напором):

85

или в общем случае для системы водоснабжения любой конфигурации, с расположением управляемых дросселей по схеме рис. 2.1, 2.2:

где Sfj – коэффициент гидравлического сопротивления фиктивного участка j;

λ – неопределенный множитель Лагранжа; Jη, Jπ – множество стоков и источников МПГС соответственно; JH – множество узлов-стоков (потребителей) с фиксированным потенциалом.

Целевая функция (2.20) сформирована на основе сопоставления полных пьезометрических напоров в энергоузлах расчетной зоны, определяемых по соответствующим двум расходам Qfj и Qfzj . Вторая группа слагаемых (2.20)

отражает традиционное условие большинства гидравлических задач, состоящих в том, что любые формы возмущений в РСВ происходят при сохранении в силе условий сплошности потоков воды.

Принципиальным является вопрос выбора независимых переменных в (2.20), каковыми являются априорно заданные значения расходов через фиктивные линии БСТГ ( Qfzj , j JH ), хотя и подверженные влиянию

субъективных факторов пользователя. Фактические расходы Qfj , j JH

независимыми не являются, будучи "связанными" моделью потокораспределения. Такой выбор упрощает структуру экстремума (минимума) целевой функции, позволяя сформировать систему нормальных уравнений:

(2.21)

86

Ниже приведен один из вариантов нормальной матрицы для МПГС

(рис. 2.1).

Вследствие большой нелинейности нормальных уравнений могут возникнуть проблемы вычислительного характера, поэтому рассматривалась вторая версия целевой функции, построенная не на законе Бернулли, а на сопоставлении расходов воды через фиктивный участок, что дало возможность существенно уменьшить нелинейность:

из которого вытекает система нормальных уравнений, размерностью mн - 1:

Как и в предыдущем случае, допускается любое другое, не повторяющееся сочетание фиктивных участков в составе (2.28).

Оптимизационная подмодель, построенная на новой версии целевой

В дальнейших исследованиях, проводившихся на основе вычислительных экспериментов, изучалось влияние (2.24) и (2.29) на конфигурацию дроссельных характеристик. Более глубокое различие между этими подмоделями не исследовалось, поскольку такая цель в работе не ставилась.

Оптимизационно-топологическая модель РСВ для рассматриваемого случая схемы замещения АП может быть сформирована объединением топологической (1.31) – (1.33) и оптимизационной (2.24) моделей (для первой версии целевой функции) в единую модель. Подобное "механическое слияние" двух моделей обусловлено, как отмечалось ранее, переводом определяющего вектора SD в разряд определяемых, с возникшим при этом дефицитом уравнений и изменением конфигурации матрицы МВС. Дополнение традиционного числа уравнений теперь уже топологической подматрицы нормальными уравнениями позволяет восстановить квадратную конфигурацию матрицы МВС, но уже на уровне оптимизационно-топологической модели, представленную ниже в матричном виде (рис. 2.1):

89