18. Кривые линии
Линия – траектория движения точки.
Вопрос: Какие вы знаете линии?
Ответ: 1)
алгебраические (
),
трансцендентные (
);
2) пространственные и плоские.
Вопрос: что определяет порядок кривой?
Ответ: Количество пересечений с плоскостью или прямой.
18.1. Касательные и нормали к пространственной кривой
Касательная
–
секущая в предельном положении.
Ч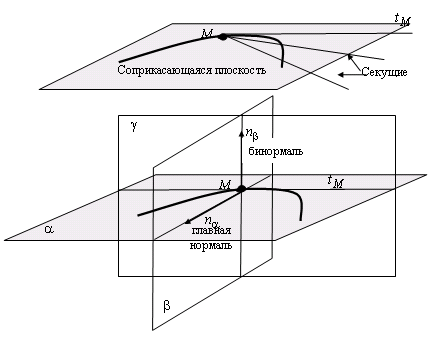
ерез
касательную можно провести множество
плоскостей и только одна из них называется
соприкасающейся плоскостью
(рис.18.1).
Рис. 18.1. Касательные и нормали проведенные к пространственной кривой
В любой точке
можно провести множество нормалей,
которые определяют нормальную плоскость
,
и только одна нормаль, лежащая в
соприкасающейся плоскости
называется главной нормалью
.
Нормаль
перпендикулярная
называется бинормалью
.
и
образуют спрямляющую плоскость
.
образуют
трехгранник Френе, при этом:
- горизонтальная плоскость;
- профильная плоскость;
- фронтальная плоскость.
1 8.1.1. Построение касательной к кривой,
проходящей через т. А.
Построениепоказано на рис. 18.2.
Рис. 18.2. Построение касательной к кривой,
проходящей через т. А
18.1.2. Построение касательной к кривой ,
проходящую через т.А.
Дано: и т. А
Проведем прямую
кривой
и проходящую через т.
(рис.18.3).Проведем ряд секущих , пересекающих и (
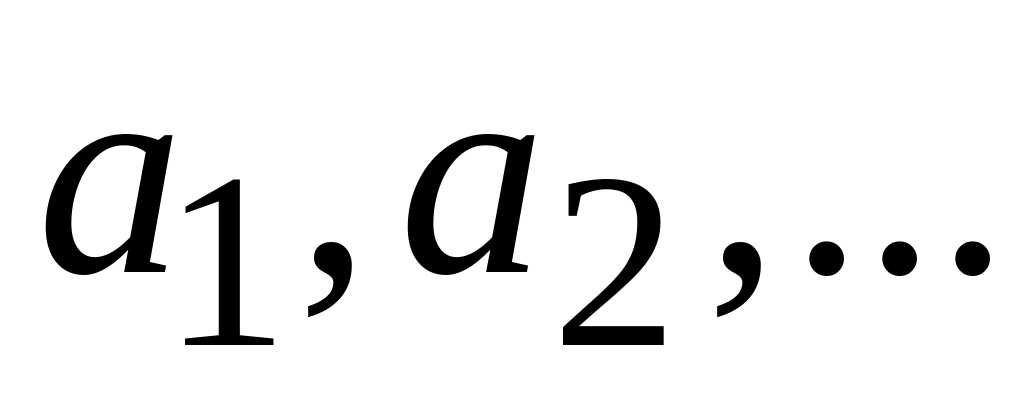и т. д.)Отложим от прямой вправо отрезки равные хордам.
Там, где огибающая пересечет - будет т.
,
соединив ее с т.
,
получим искомую касательную.
Рис. 18.3. Построение касательной к кривой
проходящей через т.А
18.1.3. Определение центра кривизны в т. М.
Дано: и т. (рис. 18.4).
1.Проведем касательные к произвольным точкам А, В, М и С.
2. Отложим на них
отрезки равной длины и соединим их в
кривую
.
3. В т.
проведем касательную
.
4. Проведем
перпендикуляры к касательным в т.
и
т.
,
пересечение которых даст центр кривизны
в т.
.
Рис. 18.4. Определение центра кривизны
18.1.4. Эволюта и эвольвента
Эволюта – множество точек, являющихся центром кривизны данной прямой.
Эвольвента.
Построение
эвольвенты показано на рис. 18.5.
Рис. 18.5. Построение эвольвенты
Эвольвента нашла широкое применение в технике: профиль зубьев у шестеренок изготавливают по эвольвенте.
Свойство: касательная к эволюте является нормалью к эвольвенте.
Для зубчатого колеса эволютой эвольвенты является окружность.
18.2. Свойства кривых линий
При построении ортогональных проекций кривых линий необходимо знать их свойства:
касательная к кривой проецируется в касательную к ее проекции (рис. 18.6);
несобственным точкам кривой соответствуют несобственные точки ее проекции.
Для плоских кривых дополнительные свойства:
порядок проекции кривой равен порядку самой кривой или оказывается на порядок ниже;
число узловых точек (т.е. точек, где кривая пересекает сама себя на проекции равно числу узловых точек на самой кривой);
кривая проекция кривой линии сохраняет тот же порядок, что и кривая линия, или оказывается кривой более низкого порядка.
Рис. 18.6. Кривая пространственая.