fd02aed

Пример 2.6. Система состоит из N = 12600 элементов, средняя интенсивность отказов которых λср = 0,32·10–6 ч–1. Необходимо определить вероятность безотказной работы в течение 50 ч и вычислить среднюю наработку до первого отказа.

Решение. Интенсивность отказов системы определяют по фор-

муле λс = λcр·N = 0,32·10–6·12600 = 4,032·10–3 ч–1. Тогда на основании

(2.16) получаем

P(50)= e−4,032 10−3 50 ≈ 0,82

и среднюю наработку до отказа

T1 = 1(4,032 10−3 )≈ 250 ч.

Пример 2.7. На испытании находилось N = 1000 образцов неремонтируемой аппаратуры. Число отказов n(∆t) фиксировалось каждые 100 ч работы (∆t = 100 ч). Данные об отказах приведены в табл. 2.2. Требуется вычислить количественные характеристики надежности.

111

Решение. Аппаратура относится к классу невосстанавливае-

мых изделий. Поэтому критериями надежности будут P*(t), a*(t),

λ*(t), T1*.

Вычислим P*(t). На основании формулы (2.6) имеем:

P* (100)=1−501000 = 0,95;

P* (200)=1−901000 = 0,91;

……………………………..

P* (3000)=1−5751000 = 0,425 .

Для расчета характеристик a(t) и λ(t) применим формулы (2.12)

и (2.15). Тогда

a* (50)= 50(1000 100)= 0,5 10−3 ч–1; a (150)= 40(1000 100)= 0,4 10−3 ч–1;

………………………………………..

a (2950)= 40(1000 100)= 0,4 10−3 ч–1;

Значения P*(t), a*(t) и λ*(t), вычисленные для всех ∆ti, приведены в табл. 2.3.

112

113

Следует иметь в виду, что в табл. 2.3 данные P*(t) приведены для концов интервалов ∆ti, а данные для a*(t) и λ*(t) – для середины интервалов ∆ti. Поэтому определение λ(t) по формуле (2.15, а) и данным табл. 2.2 не даст значений λ*(t), указанных в табл. 2.3.

Вычислим среднее время безотказной работы, предположим, что на испытании находились только те образцы, которые отказали.

По формуле (2.19, а), учитывая, что в данном случае m = tk /∆t = =3000/100 = 30 и N = 575, имеем

Полученное значение средней наработки до отказа является заниженным, т. к. опыт был прекращен после отказа 575 образцов из 1000, поставленных на испытание.

Средняя наработка на отказ (среднее время безотказной ра-

боты) − отношение суммарной наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки. В соответствии с определением средняя наработка на отказ Т0 задается формулой

где t − суммарная наработка; r(t) − число отказов, наступивших в течение времени наработки t; M {r (t)}− математическое ожида-

ние этого числа отказов.

Статистическая оценка средней наработки на отказ вычисляется по формуле

Если на испытании находится N образцов в течение времени t, то наработка на отказ вычисляется по формуле

114

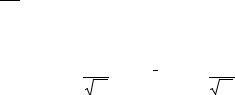
где tij − время исправной работы j-го образца изделия между (i−1) и i-м отказами; nj – число отказов за время работы tj-го образца.

Если в процессе испытаний или эксплуатации в качестве статистической оценки получена средняя наработка на отказ, то вероятность безотказной работы элемента за время t равна

где tp − время работы, tхр − время хранения. Например, устройство работает 10 ч, а общее время работы изделия – 50 ч. Следовательно, время хранения составит 40 ч.

Пример 2.8. При испытаниях некоторого устройства, имеющего время работы до отказа, распределенное по нормальному закону, получено 10 реализаций наработки до отказа (в часах): 120, 110, 80, 130, 120, 140, 80, 150, 130, 140. Требуется найти доверительные границы с доверительной вероятностью 0,95 для средней наработки на отказ и дисперсии Дх.

= 576 ч2 , S = Дx = 24 ч.

По формулам (1.22) и (1.23) определим границы средней наработки на отказ:

для tср получаем значения нижней и верхней границы средней наработки на отказ соответственно 105,4 ч и 134,6 ч. Вычисление доверительного интервала для дисперсии ведется по формуле (1.24).

Имеем N = 10, S2 = 576 ч, χкр2 (0,95; 9) = 16,92, χкр2 (0,05; 9) = 3,33 (см. табл. П2). Тогда доверительный интервал для дисперсии соста-

вит 430 ч и 1735 ч.

Параметр потока отказов − отношение математического ожидания числа отказов восстанавливаемого объекта за достаточно

115

малую его наработку к значению этой наработки. Параметр потока отказов ω(t) определяется по формуле

где r (t2), r (t1) − числа отказов к моментам времени t2 и t1 соответственно.

Для простейшего потока отказов, т. е. для потока, обладающего свойством стационарности, ординарности и отсутствия последствия, параметр потока отказов совпадает с интенсивностью отказов, т. е.

ω(t) = λ (t) = λ =const .

Рассмотрим показатели ремонтопригодности.

Вероятность восстановления − это вероятность того, что вре-

мя восстановления τ работоспособного состояния объекта не превысит заданного значения t. По определению

где Рв (t) − вероятность восстановления объекта.

Время восстановления − это то время, которое затрачивается на обнаружение, поиск места отказа и устранение последствий отказа. Вероятность восстановления представляет собой функцию распределения времени восстановления объекта, т. е. интегральный закон распределения времени восстановления, а производная по функции Рв (t) по времени дает плотность распределения случайной величины fв(t) (дифференциальный закон распределения) времени восстановления

fв (t)= d Pв (t). d t

116

Интенсивность восстановления − условная плотность вероят-

ности восстановления работоспособного состояния объекта, определенная для рассматриваемого момента времени при условии, что до этого момента восстановление не было завершено. Интенсивность восстановления μ (t) определяется по формуле

Интегрируя соотношение (2.26) в пределах (0, t), получаем

Полученное выражение устанавливает связь между интенсивностью и вероятностью восстановления для любых законов распределения времени восстановления.

Статистическая оценка интенсивности восстановления μ (t)

дание времени восстановления (Тв) работоспособного состояния объекта после отказа:

Для случая, когда процесс восстановления рассматривается как простейший [μ (t)= const] , имеет место равенство

117

Статистическая оценка среднего времени восстановления Tв задается формулой

объектов получены r возрастающих значений наработки (r < n) t1,

Считаем, что за время ti вероятность выхода из строя испытываемых N объектов составляет Pi = i/N. Для этой вероятности по табл. П5 определяем квантили up и составляем r уравнений:

Полученную систему уравнений решаем по методу наименьших квадратов. Для чего умножим левую и правую части каждого из уравнений системы на up1, up2,…, upr соответственно и все r уравнений сложим. В результате получим первое так называемое нормальное уравнение

Второе нормальное уравнение получим суммированием уравнений системы (2.32):

118

Уравнения (2.33) и (2.34) решаем относительно неизвестных T и σ и находим таким образом их оценки.

Точность полученных значений T и σ может быть оценена с помощью уравнений:

где k = (T – t0)/σ; f2 (k) и f3 (k) – вспомогательные функции, определяемые по табл. П6.

Пример 2.9. Испытания 100 ламп накаливания продолжались t0=500 ч. За время испытаний вышло из строя 5 ламп с наработкой до отказа в часах соответственно: t1 = 50, t2 = 150, t3 = 250, t4 = 300, t5 = 450. Определить среднюю наработку до отказа ламп и среднее квадратическое отклонение, полагая, что срок службы ламп подчиняется нормальному закону.

Решение. Для вероятностей 0,01; 0,02; 0,03; 0,04; 0,05 по табл. П5

находим квантили ирi :

ир1 = –2,33; ир2 = –2,05; ир3 = –1,88; ир4 = –1,75; ир5 = –1,64.

Составляем уравнения:

T – 2,33σ = 50,

T – 2,05σ = 150,

T – 1,88σ = 250,

T – 1,75σ = 300,

T – 1,64σ = 450.

Для решения данной системы уравнений складываем их и получаем

5T – 9,65 σ = 1200.

Затем, умножая исходные уравнения на коэффициенты при σ и суммируя, получаем

9,65T – 18,90 σ = 2160.

119

Решая нормальные уравнения, находим Т≈1315 ч, σ = 557 ч. Для оценки точности полученных значений T и σ определяем

k = 1315 −500 =1,46 . 557

По табл. П6 находим: f2 (1,46) = 33,34; f3(1,46) = 11,55.

Тогда

Откуда σ(T ) = 320 ч, σ(σ)=190 ч.

Как видно, точность определения параметров распределения в условиях данного примера невысокая. Доверительные интервалы величиной ±2σ, что соответствует вероятности приблизительно 95 %, в данном случае составляют:

T ± 2σ(T )=1315 ± 2 320 ч, σ ± 2σ(σ)= 557 ± 2 190 ч.

В табл. 2.4 приведены расчетные значения показателей надежности основных элементов СЭС и их условные обозначения. Данные носят ориентировочный характер.

Коэффициент готовности – вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается.

Из определения следует, что коэффициент готовности характеризует готовность объекта к применению по назначению только в отношении его работоспособности. Это означает вероятность застать объект в работоспособном состоянии в произвольный период времени, причем этот момент не может быть выбран в тех интервалах, где применение объекта исключено, например при проведении плановых регламентных работ.

120