fd02aed

Основными параметрами закона Релея являются:

•Rср − среднее арифметическое переменной случайной вели-

чины;

•σRс −среднее квадратическое отклонение Rc;

•σ − среднее квадратическое отклонение значений координат х

иу конца радиус-вектора Rc.

Они связаны между собой следующими соотношениями:

Фактическое поле рассеяния значений переменной величины радиус-вектора Rc находят из выражения:

61

При распределении Релея, когда фактическое поле рассеяния превосходит поле допуска (ω > δ), возможно появление брака

(см. рис. 1.26).

Общую площадь F(Rc), ограниченную кривой распределения, находят по интегральному закону распределения эксцентриситета:

который после подстановки величин t = Rc/σпринимает нормированный вид

и табулируется аналогично функции Лапласа (см. табл. П3). Пример 1.5. Рассчитать вероятный процент брака, если допуск

на изготовление детали равен δ = 0,04 мм. В результате непосредственных измерений первых 25 деталей установлено среднее квадратическое отклонение S = 0,009 мм.

Решение. Расчетное значение среднего квадратического отклонения находим по формуле σ = kσ S и табл.1.3:

σRc = σ = kσ·S = 1,4·0,009 = 0,0126 мм.

Фактическое поле рассеяния значений эксцентриситета – по формуле (1.60):

ω = 5,252σRc = 5,252·0,0126 = 0,0662 мм.

При Rc= δ = 0,04 мм и t = 0,655δ /σRc = 0,655·0,04/0,0126 = 2,08.

В соответствии с табл. П3 Ф(t) = 0,8851, т. е. количество годных деталей составляет 88,51 % и количество брака – оставшиеся 11,49 %.

1.9.9.Треугольный закон распределения (закон Симпсона)

Краспределению по закону Симпсона приводит сложение двух случайных величин, подчиненных закону равной вероятности при одинаковых параметрах рассеяния. Кривая рассеяния имеет вид

62

равнобедренного треугольника (рис. 1.27), из-за чего закон Симпсона часто называют законом треугольника.

При выборе в качестве начала отсчета случайной величины ее плотность распределения и математическое ожидание имеют следующий вид:

1.10. Статистическое регулирование технологического процесса

Под статистическим регулированием технологического процесса понимается корректировка параметров процесса в ходе производства с помощью выборочного контроля изготовляемой продукции для обеспечения требуемого качества и предупреждения брака.

Для статистического регулирования процесса применяется ме-

тод медиан и индивидуальных значений и метод средних арифметических значений и размахов.

63

Первый из этих методов рекомендуется при отсутствии автоматических измерительных средств, второй – при наличии автоматических устройств для контроля.

Медианой x называется срединное значение упорядоченного по возрастанию или убыванию ряда чисел.

Из потока продукции через определенный промежуток времени периодически отбирают выборку объемом 3…10 единиц (чаще всего в 5 единиц). Период времени между двумя выборками устанавливается опытным путем. Он зависит от стабильности процесса и обычно составляет 1…2 ч.

Результаты контроля наносят на карту (рис. 1.28), которая имеет две внешние сплошные горизонтальные линии, ограничивающие поле допуска Tв и Tн и четыре предупредительные: Pв и Pн – границы регулирования медиан (внутренние границы, ограничивающие поле предупреждения); Pв.р и Pн.р – границы крайних значений данной выборки.

Положение предупредительных границ рассчитывается по формулам:

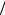Pв = Тв −0,8 А δ2 ; Pн = Тн + 0,8 А δ2;

(1.65)

Pв.р = Тв − В δ2 ; Pн.р =Тн + В δ2,

64

где 0,8 − поправочный коэффициент; A и B − коэффициенты, зависящие от объема выборки (N), определяются на основе теоретических положений статистического контроля (при N = 5, A = 0,559,

B = 1,65); δ − допуск.

На карту наносят результаты замеров в виде точек за исключением третьего измерения (N = 5), которое отмечается крестиком (согласно рис. 1.28, например, результаты замеров в первой выбор-

ке 37,97; 37,97; 37,98; 37,99; 37,99; размер 37,98 является третьим и отмечается крестиком).

Протекание процесса считается удовлетворительным, если медианы x не выходят за границы Pв и Pн, а крайние значения выборок – за границы Pв.р и Pн.р. При таком процессе продукцию, изготовленную между данной и предыдущей выборками, принимают без дополнительного контроля. Если же имеются выходы точек за границы регулирования, то процесс считается неудовлетворительным. Например, выборки 4, 5 и 6 вышли за границы Pв и Pв.р, а выборка 7 – за границы Pн и Pн.р. В этом случае дают сигнал предупреждения, на карте делают отметку в виде стрелки и устраняют причину, вызвавшую отклонения процесса от нормального хода. Продукция, изготовленная между двумя выборками, подлежит сплошному контролю.

По второму из этих методов (средних арифметических значений и размахов) отбирают выборки объемом 3…10 единиц. Статистическими характеристиками при этом методе являются среднее арифметическое значение x и размах варьирования R данной выборки, определяемые по формулам:

где xi − результат замера контролируемого параметра; n − число замеров в выборке; xmax и xmin − наибольшее и наименьшее значения в выборке.

Результаты замеров и расчетов значений x и R изображают графически. В верхней части карты (рис. 1.29) нанесены графически средние арифметические значения x .

65

При удовлетворительном протекании процесса x не должны выходить за границы регулирования Pв и Pн, а размахи – за свою границу Pв.R. Предупредительные границы регулирования сигнализируют о возможности возникновения брака. Выборки 4, 5 и 6 сигнализируют о разладе процесса.

Границы Pв и Pн определяют по формулам:

Границу для размахов определяют по формуле

1.11. Проверка статистических гипотез

На разных стадиях статистического исследования часто возникает необходимость в экспериментальной проверке некоторых предположений (гипотез). Например, необходимо убедиться, что измеряемые величины нормально распределены. Наша цель состоит

втом, чтобы проверить, не противоречит ли высказанное предположение (гипотеза) имеющимся выборочным данным.

Для количественного сопоставления эмпирического (статистического) и теоретического распределений или, иными словами, для того, чтобы принять или отвергнуть ту или иную статистическую гипотезу, используют результаты наблюдений. Пусть n наблюдений

представлены последовательностью х1, х2, …, хn. Тогда для проверки статистической гипотезы все пространство наблюдений разделяют

на два непересекающихся подмножества Rn1 и Rn2, т. е. Rn1 ∩ Rn2 = 0. Проверяемую гипотезу принимают по результатам наблюдений, если выборочная точка последовательности (х1, х2, …, хn) попадает

вобласть Rn1, и отвергают при попадании этой точки в подмножество Rn2, которая носит название критической. Выбор этой области однозначно определяет и область Rn1.

Статистическая гипотеза характеризует поведение наблюдаемых признаков и является утверждением о параметрах распределе-

ния исследуемого признака (например, о среднем, дисперсии и т. д.). Такая гипотеза называется параметрической. Гипотеза о характере вида распределения случайной величины называется непа-

раметрической.

67

Правило, по которому применяется или отклоняется выдвинутая гипотеза, называется статистическим критерием. Процедура обоснованного сопоставления высказанной статистической гипотезы с имеющимися в нашем распоряжении выборочными данными осуществляется с помощью того или иного статистического крите-

рия и называется проверкой статистических гипотез.

Правило, по которому строится тот или иной статистический критерий, состоит в том, что выбирается некоторая функция f(Θ) = F(х1, х2, …, хn), которая является мерой расхождения между измеренными и предполагаемыми теоретическими значениями исследуемой величины. Эта функция является случайной величиной и называется статистикой критерия. Закон распределения статистики критерия Θ позволяет с заданной вероятностью принять или отклонить выдвинутую гипотезу.

Особый интерес представляет простой случай, когда среди параметров распределения случайной величины неизвестным является один, причем этот параметр может принимать лишь два конкретных значения Θ0 и Θ1.

Пусть Θ0 – желаемое («хорошее») значение параметра Θ, а Θ1 – нежелаемое («плохое») значение. Задача формулируется как проверка гипотезы о том, что Θ = Θ0. При проверке статистических гипотез эта выдвигаемая гипотеза обычно обозначается Н0 (нулевая гипотеза). Тогда гипотезу о том, что Θ = Θ1, называют конкури-

рующей (альтернативной) и обозначают Н1.

При проверке гипотезы Н0 против Н1 возможны два рода ошибок. Ошибка первого рода – это ошибка, когда отвергается верная гипотеза Н0. Ошибка второго рода – это ошибка, когда принимается неверная гипотеза Н1.

Вероятность ошибки первого рода обозначим γ1 = Р (отвергается Н0 | верна Н0). Символически можно записать в следующем виде:

т. е. вероятность ошибки 1-го рода γ1 есть вероятность принадлежности искомой выборки критической области Rn2 при условии истинности рассматриваемой гипотезы Н0.

68

Ошибку второго рода обозначим γ2 (принимается Н0 | верна Н1). Ошибка второго рода с вероятностью γ2 состоит в том, что принимается неверная гипотеза Н0, в то время как в действительности верна конкурирующая гипотеза Н1, что символически записывается

т. е. вероятность ошибки 2-го рода γ2 есть вероятность принадлежности искомой выборки области допустимых значений Rn1, при условии истинности конкурирующей гипотезы Н1. Величину 1 − γ1, т. е. вероятность того, что гипотеза Н0 будет отвергнута, когда она ошибочна, называют мощностью критерия и обозначают π.

В литературе величину γ1 иногда называют риском изготови-

теля, а величину γ2 − риском заказчика или потребителя.

Ошибку 1-го рода по аналогии с ошибкой при определении доверительного интервала называют уровнем значимости, тогда величина 1–γ1 будет доверительной вероятностью, т. е.

1− γ1 = P[(x1, x2 ,..., xn ) Rn1 H0 ].

Доверительная вероятность − это вероятность не совершить ошибку и принять верную гипотезу Н0. Вероятность отвергнуть ложную гипотезу Н0 называют мощностью критерия, т. е.

1− γ2 = P[(x1, x2 ,..., xn ) Rn2 H1 ].

Альтернативная гипотеза может принимать различные значения в зависимости от существа решаемых задач. Рассматриваемую как функцию от произвольного значения Θ вероятность отвержения нулевой гипотезы, когда справедлива альтернативная Θ1, называют

функцией мощности критерия.

Чем больше мощность критерия, тем меньше вероятность совершения ошибки второго рода γ2. Во всех случаях мощность критерия увеличивается при увеличении объема выборки.

В заданном объеме выборки невозможно одновременно сделать γ1 и γ2 сколь угодно малыми, поэтому, выбрав тем или иным способом критическую область γ1, находят критическую область Rn2, для которой величина ошибки γ2 принимает минимальное значение.

69

Различают простые и сложные гипотезы. Статистическая гипотеза называется простой, если она однозначно определяет распределение исследуемого признака, в противном случае гипотеза называется сложной. Например, простой гипотезой является утверждение о том, что изучаемый признак X имеет нормальный закон распределения со средним значением, равным нулю, и единичной дисперсией. Если же высказывается предположение, что наблюдаемый признак X имеет нормальное распределение (не указываются при этом конкретные значения среднего и дисперсии или указывается значение только одного параметра), то это сложная гипотеза.

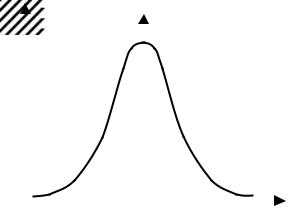
Распределение статистики критерия Θ позволяет найти области принятия и отклонения гипотез. Задавая критические значения Θ1–γ1/2 и Θγ1/2 (рис. 1.30), получаем области отклонения гипотезы (критические области). Точки Θ1–γ1/2 и Θγ1/2 называют критическими точками или квантилями, а интервал между ними – интеркван-

тильным. Величина γ1 является уровнем значимости критерия и обычно выбирается достаточно малой. Наиболее часто задают величину γ1 = 0,1÷0,001. На рис. 1.30 величина γ1 равна сумме заштрихованных площадей.

Рис. 1.30. Распределение статистики критерия Θ

70