fd02aed

где F(x) – интегральная функция распределения (рис. 1.1), определяющая вероятность того, что случайная величина примет значения, не превосходящие хi.

Ее задание и определяет закон распределения случайной величины Х. В общем случае функция распределения F(x) может быть как разрывной, так и непрерывной. Конкретные виды функции распределения для некоторых важных распределений будут рассмотрены ниже.

В большинстве практически важных случаев распределение недискретных случайных величин может быть задано в другой форме с помощью введения функции плотности вероятностей f(x).

F(x)

1

F(x2)

F(x1)

Рис. 1.1.

Интегральная функция распределения

Характерной особенностью случайной величины является то, что заранее не известно, какое из значений она примет. Возможность принятия случайной величиной Х значения из элементарного интервала (х1, х2) количественно оценивается вероятностью

f (х) − плотность распределения случайной величины; x2= x1+dх. Плотность f(х) является важнейшей характеристикой, задаю-

щей распределение случайной величины. Плотность удовлетворяет двум условиям: она неотрицательна и интеграл от нее в полных пределах изменения аргумента х равен единице:

21

−∞

Как видно из формулы (1.1), функция распределения F(х) выражается через плотность f(х):

−∞

Сдругой стороны, если плотность f(х) непрерывна в точке х, то

еезначение в этой точке равно производной от функции F(х):

При этом предположении функция распределения F(x) будет являться первообразной для плотности f(x). Поэтому

x2

P(x1 < x < x2 )= ∫ f (x) dx = F(x)= F(x2 )− F(x1 ).

x1

f(x) называют также дифференциальной функцией распределения.

Из свойств плотности f(x) и определения функции F′(x) следует, что последняя – неотрицательна, не убывает и равна 0 и 1 при значении аргумента –∞ и ∞:

F(х)≥0; F(х1 ) ≥ F(х2) при x1 > х2; F(– ∞ )=0; F( ∞ )=1.

График плотности распределения f(x) называется кривой рас-

пределения случайной величины. Исходя из геометрической интер-

претации интеграла как площади соответствующей криволинейной трапеции, заключаем, что для произвольного –∞ < х0 < ∞ число F(x0) равно площади под кривой распределения, лежащей левее прямой х=х0. АналогичноинтерпретируетсявероятностьP(x1<x≤ x2) (рис. 1.2).

Случайная величина X, для которой существует плотность распределения f(x), называется непрерывной.

Если под случайной величиной X понимать продолжительность безотказной работы объекта, то произведение f(х)dх есть вероятность отказа объекта в интервале времени (х1, х2). Значение функции распределения F(х) равно вероятности отказа объекта до момента х. В теории надежности часто употребляют такое понятие, как вероятность безотказной работы Р(х), которое является дополнительным понятием к функции распределения F(x).

22

Функция Р(х) называется также функцией надежности. Примерные графики функции распределения F(х) и функции надежности Р(х) изображены на рис. 1.3.

На практике часто располагают дополнительной информацией о том, что случайная величина превысила некоторое значение х (в частности, это изделие проработало время x и не отказало).

Разумеется, эта информация изменяет возможность принятия случайной величиной тех или иных значений. В связи с этим вводят специальную функцию − интенсивность отказов λ(x). Значение

интенсивности отказов в точке х, умноженное на dх, равно вероятности принятия случайной величиной значения из элементарного интервала (х1, х2) при условии, что эта случайная величина X больше х:

λ (х)dx = P{x < X ≤ x + dx|X > x},

где символ «|» означает «при условии, что…».

В нашем контексте λ(х)dх есть вероятность отказа изделия сразу после момента времени х, если оно до этого не отказало.

1.2. Меры положения и рассеяния кривой распределения

Кривая распределения плотностей вероятностей случайной величины характеризуется своим положением на оси абсцисс и рассеиванием случайной величины. Для оценки положения и рассеяния кривой распределения вводятся соответствующие критерии или

меры.

Кмерам положения относятся: мода, математическое ожида-

ние и медиана случайной величины.

Кмерам рассеяния относятся: стандартное отклонение, дисперсия и размах.

Функция распределения плотности вероятностей может иметь одно или несколько максимальных значений в разных местах области (рис. 1.4). Значение случайной величины X, при котором f(x) принимает максимальное (наиболее вероятное) значение в окрестности какого-либо значения случайной величины х, называется мо-

дой распределения (Mо).

24

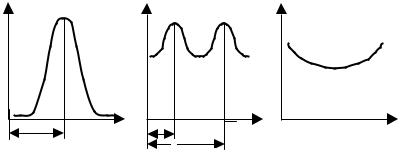
Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений:

Рис. 1.4. Кривые распределения случайной величины X: а – одномодальная; б – двухмодальная; в – антимодальная

Это определение справедливо для дискретных случайных величин. Для непрерывных величин математическое ожидание случайной величины X, имеющей плотность распределения f(х), вычисляется по формуле

−∞

Статистической оценкой математического ожидания является среднее арифметическое значение случайной величины

Математическое ожидание (среднее арифметическое значение) случайной величины называют часто центром рассеяния или центром группирования случайной величины. Математическое ожидание является оценкой истинного значения измеряемой величины.

25

Медианой случайной величины (Ме) называется значение, для которого

Р(х < Ме) = Р(х > Ме),

т. е. вероятность появления случайной величины, меньшей, чем медиана, или большей, чем медиана, одинакова (рис. 1.5).

Геометрическая медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам:

Мерой рассеяния случайной величины Х около ее среднего

26

Когда оценка стандартного отклонения осуществляется на основе статистических данных, ее называют выборочным средним квадратическим отклонением, обозначают буквой S и определяют по формуле

∑n (xi − x )2

С целью экономии времени и уменьшения ошибок при подсчетах S, когда n велико, а хi – большие или нецелые числа, следует использовать тождество

Другая мера рассеяния – дисперсия (дисперсия и означает рассеивание) характеризует разброс значений случайной величины относительно ее математического ожидания. Дисперсия увеличивается с увеличением рассеяния результатов наблюдения.

Дисперсия определяется по формуле

−∞

где хi – непрерывная случайная величина.

Дисперсия эмпирических данных вычисляется по формуле

Дисперсия обладает следующими свойствами:

•Дх ≥ 0;

•Дх ·С = 0 для С = const (дисперсия неслучайной величины рав-

на нулю);

27

•Д (СХ) = С2·Дх – неслучайную величину можно выносить за знак дисперсии, возведя ее в квадрат;

•Дх = Мx(X 2) – (Мх)2 – дисперсия равна математическому ожиданию квадрата случайной величины минус квадрат ее математического ожидания;

•Д(Х+Y) = Дх + Дy, если Х и Y – независимые случайные вели-

чины.

Последнее свойство рассмотрим более подробно на примере двух случайных величин X и Y. По определению

Д(X +Y )= M [(X +Y )− M (X +Y )]2 .

После раскрытия квадратных скобок и объединения каждой случайной величины со своим математическим ожиданием получим

Д( Х +Y ) = M (X − M x )2 + M (Y − M y )2 + 2M [(X − M x )(Y − M y )],

откуда

Д( Х +Y ) = Дх + Ду + 2cov(XY ),

где cov(XY) = M [(X – Mх)(Y – My)] = M (XY ) – МхМy.

Величину, определяемую формулой (1.13), называют ковариацией. Она характеризует связь между случайными величинами X и Y. Для независимых случайных величин ковариация равна нулю. Ковариация является неудобной характеристикой, т. к. по ее величине трудно судить о степени (тесноте) связи. Поэтому была введена другая величина – коэффициент корреляции, вычисляемый по формуле

Коэффициент корреляции меняется в пределах от –1 до +1 и является характеристикой тесноты линейной связи между двумя случайными величинами. Если Y и Х независимы, то ρ(XY )= 0 . Ес-

ли абсолютное значение ρ(ХY) окажется больше 1, то совершенно ясно, что произошла ошибка и необходимо пересчитать результат. В случае сильной положительной корреляции достигается значение,

28

близкое к +1, а при сильной отрицательной корреляции достигается значение, близкое к –1. Таким образом, когда |ρ(ХY)| близок к 1, это указывает на сильную корреляцию между X и Y, а когда |ρ(ХY)| близок к 0 – на слабую корреляцию.

Переходя от случайных величин X и Y к их значениям x и y, коэффициент корреляции по результатам статистических испытаний можно вычислить по формуле

n – число пар данных.

Пример1.2. Найтикоэффициент корреляцииподанным табл. 1.1.

Решение. Используя данные, приведенные в табл. 1.1, определяем дисперсии и коэффициент корреляции:

Дхх = 2312,02 – 263,22/30 = 2,88; Дyy = 23,97833 – 26,8162/30 = =0,00840;

cov(xy) = 235,3570 – (263,2·26,816)/30 = 0,0913; ρ(xy) = = 0,0913/ 2,88 0,0084 = 0,59.

Значение ρ(xy) оказалось равным 0,59, следовательно, существует некоторая положительная корреляция между x и y.

29

Размах случайной величины R определяется как разность между наибольшим и наименьшим значениями случайной величины:

30