fd02aed

Рассмотрим часто применяемый критерий согласия χ² (критерий Пирсона) для проверки статистических гипотез. Суть этого критерия состоит в следующем. Пусть нужно проверить гипотезу Н0, состоящую в том, что результаты наблюдений образуют выборку из n значений Х – случайной величины, которая имеет некоторое заданное теоретическое распределение. Ставится задача – определить, насколько близко выборочное распределение случайной величины к ее теоретическому распределению.

Для решения этой задачи все пространство значений наблюдаемой величины разобьем на непересекающиеся области S1, S2, …, Sk. Обозначим через Pi вероятности попадания (при заданном распределении) в области Si , а через mi – число попавших в эти области наблюдений (частоты).

По данным наблюдений и с учетом теоретического распределения случайной величины определим:

На практике при применении критерия согласия χ² пространство выборок разбивают не менее чем на пять непересекающихся областей Sk (k ≥ 5), а число реализаций, попавших в область, должно быть не менее десяти. Для χ²-распределения вычислены таблицы

вероятностей P = P(χнабл2 < χкр2 ) (см. табл. П2). При использовании

таблицы следует иметь в виду следующее. Если в качестве теоретического распределения задано однопараметрическое распределение, то берут число степеней свободы, равное f = k – 1. Если задано многопараметрическое распределение, то число степеней свободы принимают равным f = k – p – 1, где p – число неизвестных параметров.

71

По значению χнабл2 , вычисленному по формуле (1.71), и известному числу степеней свободы f, используя табл. П2, находят P. Если значение P близко к единице, т. е. χ02,9 , χ02,99 , ..., χ02,999 , то вероятность того, что χ2 > χкр2 мала, и, следовательно, гипотезу Н0 нужно

отбросить.

Для применения критерия χ² применяют метод, когда полученные данные группируют по интервалам частот и сравнивают с ожидаемым числом наблюдений для принятого распределения. На основе этого сравнения вычисляют критерий, который приближенно следует χ²-распределению только в том случае, если модель выбрана правильно. Если модель выбрана неправильно, то значение критерия превысит значение случайной величины, распределенной по закону χ². Для оценки правильности принятой модели используют

численные значения процентилей χ2P( f ) – распределения, приведен-

ные в табл. П2.

Критерий Пирсона вычисляют по формуле

где k − число сравниваемых частот; mi и mi' − эмпирическая и теоретическая частоты в i-м интервале.

Полученные статистические данные делят таким образом, чтобы в каждый интервал попадало не менее пяти наблюдений. Если в каком-либо интервале число наблюдений окажется меньше пяти, то его объединяют с соседним интервалом таким образом, чтобы ожидаемое число наблюдений в объединенном интервале было не менее пяти.

Расчет значений χнабл2 удобно выполнять в форме табл. 1.6. После заполнения всей таблицы вычисляется число степеней свободы:

f = k – p – 1 ,

где k – число сравниваемых частот (в нашем примере k = 7); p – число параметров теоретического распределения (для нормального закона p = 2). В нашем примере f = 7 – 2 – 1 = 4.

72

Область допустимых значений критерия χ2 или область принятия гипотезы характеризуются неравенством

χ2набл < χ2кр (γ1, f ) ,

где χ2набл – значение критерия, вычисленное по данным наблюдений; χ2кр(γ1, f) – критические значения критерия при заданных γ1 и f; γ1 – уровень значимости в технике, обычно принимается равным 0,05.

73

По табл. П2 находим χ2кр (0,05; 8) = 15,5. Поскольку 5,88 < 15,5,

гипотеза о нормальном распределении анализируемой погрешности справедлива.

Используя метод разбиения на интервалы, можно определить вероятность попадания случайного наблюдения в i-й интервал из соотношения

где xiн − нижняя граница i-го интервала; xiв − верхняя граница i-го

интервала; k – число интервалов.

Границы интервала х1, х2, …, хk определяют с помощью теоретического распределения с использованием следующих оценок параметров:

Нижняя граница первого интервала и верхняя граница последнего интервала являются соответственно наименьшим и наибольшим значениями, которые может принимать случайная величина. Границы интервалов установлены таким образом, что для каждого интервала вероятность попадания случайной величины в него оценивается как 1/k.

Математическое ожидание Мхi числа наблюдений в каждом интервале для принятой теоретической модели определяют таким образом:

Подсчитывают число наблюдений в каждом интервале mi и вычисляют критерий:

Сравнивают вычисленное значение χнабл2 с табличным значением для заданного уровня значимости и числа степеней свободы. Если вычисленное значение χнабл2 превышает его табличное значение для α = 0,95, то вероятность того, что полученные данные имеют принятое распределение, не превышает 0,05, и модель отвергают как не удовлетворяющую требованиям.

74

Кроме того, можно пользоваться критерием Романовского:

Если АР < 3, гипотеза принимается. Если АР > 3, гипотеза отвергается.

В нашем случае AР = (5,88 −8) 2 8 = 0,53, следовательно, эм-

пирическое распределение соответствует нормальному закону. Если теоретические значения параметров известны, то лучшим

является критерий Колмогорова λк:

где Dк – наибольшее отклонение теоретической кривой распределения от экспериментальной; N – общее количество экспериментальных точек.

При неизвестных параметрах этот критерий также применим, но в этом случае дает несколько завышенные оценки.

Применение данного критерия рассмотрим на примере, представленном в табл. 1.7.

75

В колонках 4 и 5 табл. 1.7 приведены накопленные суммы, которые образуются путем прибавления последующих частот к сумме предыдущих. Затем составляется разность между накопленными теоретическими и накопленными эмпирическими суммами (колонка 6) и находится максимальное значение этой разности. В данном примере она равна 7,38.

После этого находим

Dmax = 7,38/N = 7,38/200 = 0,037, N = ∑mi = 200.

Коэффициент λк находится по формуле

λк = Dmax N = 0,036· 200 = 0,50904.

Пользуясь табл. 1.8 для данного значения λк, находим Р(λ) – вероятность того, что гипотетическая функция выбрана правильно. Для λк = 0,5 имеем Р(λ) = 0,9639, т. е. эмпирическая и теоретическая кривая согласуются.

Таблица 1.8 Таблица значений Р(λ) критерия Колмогорова

76

Пример 1.6. В процессе испытаний десяти генераторов были зафиксированы следующие значения наработок между отказами,

выраженные в часах: 2, 4, 4, 5, 5, 5, 6, 8, 8, 10, 12, 12, 15, 15, 16, 16, 18, 18, 19, 20, 21, 21, 21, 21, 22, 22, 22, 22, 23, 23, 23, 23, 23, 24, 24, 24, 24, 24, 24, 24, 2, 3, 4, 4, 4, 4, 5, 5, 5, 6.

Испытания генераторов проводились в течение t = 500 ч, при этом весь период разбит на пять интервалов. Первые десять реализаций зафиксированы на первом интервале (0, t1) = 100 ч, вторые десять реализацийзафиксированы на втором интервале (t1, t2) = 100 ч и т. д. В качестве теоретического распределения наработки между отказами принят экспоненциальный закон с параметрами потока отказов (параметром распределения на каждом участке, равном λi). Ставится задача – провести проверку соответствия статистических данных наработок между отказами теоретическому распределению с помощью критерия χ2.

Решение. Для вычисления квантиля χ2-распределения воспользуемся формулой (1.70):

Статистические данные разобьем на пять интервалов, и тогда в каждый интервал попадет по десять реализаций, т. е. m1 = m2 =…= = mi =10. Общее число реализаций в процессе испытаний: n = 50. Вероятность отказа на каждом участке (интервале) соответствует параметру интенсивности отказов на данном участке, который определяют по формуле

Pi = λi = ∑miti .

Вычислим λi для каждого интервала:

λ1 = ( 10 ) = 0,17; 2 + 4 + 4 +5 +5 +5 +6 +8 +8 +10

λ2 = ( 10 ) = 0,06; 12 +12 +15 +15 +16 +16 +18 +18 +19 + 20

77

Принимая в качестве теоретического закона экспоненциальное распределение, найдем число степеней свободы: f = k – 1 = 5 – 1 = 4. Затем для числа степеней свободы f = 4 и квантиля χнабл2 = 73,3 по табл. П2 определим, что вероятность P > 0,999. Следовательно, гипотезу об экспоненциальном распределении для P > 0,999 следует

отбросить, т. к. χкр2 (18,5) < χнабл2 (73,3).

Пример 1.7. По результатам эксплуатации двадцати приборов (n = 20) получены статистические данные о наработке до отказа каждого из них (табл. 1.9). На основе этих данных определить вероятность безотказной работы прибора за 10 ч, предполагая, что время безотказной работы распределено по экспоненциальному закону с помощью критерия χ2.

Таблица 1.9 Время работы ti до отказа каждого из 20 приборов

78

Решение. Предположив экспоненциальный закон распределения времени работы прибора до отказа, найдем оценку параметра интенсивности отказа:

λ = ∑nti ; λ = 444420 = 0,0045 ч–1.

На основании того, что n = 20, число интервалов выбираем рав-

ным n/5, поэтому k = 20/5 = 4.

Для функции экспоненциального распределения F(t,λ)=1−e−λt находим границы интервалов, полагая, что:

P(x ≤ x1 )=1−e−0,0045x1 =1k = 0,25;

P(x ≤ x2 )=1−e−0,0045x2 = 2k = 0,50;

P(x ≤ x3 )=1−e−0,0045x3 = 3k = 0,75;

P(x ≤ x4 )=1−e−0,0045x4 = 4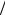k =1,00.

Решая эти уравнения относительно x1, x2, x3, x4, находим интервалы:

x3 = 0,00450,75 =165,5; x4 = 0,00451,00 = 222,0 .

Поскольку экспоненциально распределенная случайная величина при λ = 0 изменяется от 0 до ∞, нижняя граница первого интервала равна нулю, а верхняя граница последнего интервала равна ∞. Вероятность попадания случайной величины в любой из интервалов равна 0,25. Исходя из данных табл. 1.9, примем x1 = 61; x2 = 152; x3 = 300 и составим таблицу (табл. 1.10).

79

Таблица 1.10

Сравнение фактических и ожидаемых данных, сгруппированных в интервалы

Математическое ожидание числа наблюдений в интервале для принятой математической модели находят по формуле (1.75), оно составляет: Mxi = N/k = 20/4 = 5 для i = 1, 2, 3, 4. Фактическое число mi наблюдений в i-м интервале находят непосредственно по исходным наблюдениям, приведенным в табл. 1.5. Сравнение величин mi и Mxi дано в табл. 1.6.

Используя формулу (1.71), вычислим значение χнабл2 :

Поскольку для экспоненциального распределения находили оценку одного параметра, значит p = 1. Отсюда число степеней свободы равно f = k – p – 1 = 4 – 1 – 1 = 2. По табл. П2 для двух степеней свободы находим:

P [χкр2 (2)> 6,0]= 0,05 или P [χкр2 (2)> 4,6]= 0,10.

Следовательно, вероятность получить значение χнабл2 = 5,2

для принятой теоретической модели заключена между 0,05 и 0,10. Таким образом, следует отвергнуть гипотезу об экспоненциальном законе распределения наработки прибора до отказа. Гипотеза об экспоненциальном законе распределения отвергается с вероятностью 0,9.

80