fd02aed

1.3. Начальные и центральные моменты

Чтобы характеризовать случайные погрешности, часто пользуются некоторыми числовыми вероятностными характеристиками случайных погрешностей, которые называют начальным и центральным моментами. Моменты представляют собой некоторые средние значения и называются начальными, если усредняются величины, отсчитываемые от начала координаты, и центральными – от центра функции плотности вероятности.

Первый начальный момент функции распределения плотности вероятностей совпадает с математическим ожиданием результатов наблюдений:

i=1

Первый центральный момент результатов наблюдений равен нулю. Значение стандартного отклонения σ носит название второго центрального момента распределения относительно математического ожидания (среднего арифметического значения) случайной величины. Второй центральный момент (дисперсия результатов на-

блюдений) определяется как

i=1

Вобщем случае момент дискретной случайной величины r-го порядка можно представить в виде

i=1

где а – постоянная величина.

Если а = 0, то момент называют начальным, если а = Мх или а = х r – центральным. Нечетные центральные моменты указывают на симметрию распределения относительно математического ожидания. У всех симметричных распределений нечетные моменты относительно среднего значения равны нулю.

31

Для более подробного описания распределения используются моменты более высоких порядков.

Третий центральный момент (М3) характеризует асимметрию распределения случайных погрешностей, т. е. скошенность (рис. 1.6).

Коэффициент асимметрии:

Четвертый центральный момент (М4) характеризует форму

(крутизну кривой), плосковершинность или островершинность распределения случайных погрешностей (рис. 1.7) и описывается с по-

мощью эксцесса:

Число 3 вычитают потому, что для нормального распределения погрешностей M4 = 3, следовательно, Ek = 0, т. е. в качестве кривой с нулевым эксцессом принята кривая нормального распределения.

32

Выражение 1/ Ek называется контрэксцессом. Если Ek > 0,

то говорят, что имеется положительный эксцесс, т. е. вершина кривой находится выше кривой нормального распределения. Если Ek < 0 – имеется отрицательный эксцесс и вершина кривой находится ниже вершины кривой нормального распределения.

Вслучаях, когда значения случайной величины xi заданы трех-

иболее значимыми числами и объем выборки N > 25, расчет параметров целесообразно вести путем введения случайной величины

xi′ = xi −h x0 ,

где xi′ – новая случайная величина; h – величина интервала; х0 – не-

которое начальное значение (обычно принимают середину средних

значений xi).

Последовательность вычисления рассмотрим на примере табл. 1.2. Вычислим среднее значение, среднее квадратическое отклонение, асимметрию и эксцесс.

Таблица 1.2

Среднее значение, среднее квадратическое отклонение, асимметрия и эксцесс

В табл. 1.2 через xi обозначены середины интервалов.

33

и показатель эксцесса (крутизну):

E= m4 −3 = 2,52 −3 = −0,48.

m22

Рассмотренные числовые характеристики являются основными. Конечная цель при исследовании распределения случайной величины – установление уравнения кривой распределения.

34

1.4.Коэффициенты относительного рассеяния

иотносительной асимметрии

Во многих технических приложениях функции распределения характеризуются коэффициентом относительного рассеяния, коэффициентом относительной асимметрии и величиной практически предельного поля рассеяния.

Положим, что погрешности отклонений размеров изделий от их номинального значения заданы функцией плотности f(х) и величинами параметров Mх, Дх (рис. 1.8). Примем номинальное значение за начало координат.

Рис. 1.8. Функция распределения

Практически предельным полем рассеяния называется расстояние между такими двумя значениями х1 и х2 случайной величины, при которых площадь, ограниченная кривой, осью абсцисс и отрезком [х1, х2], равна 1 − β, где β – вероятность риска (брака). Обычно принимают β = 0,0027. По определению можно написать:

x∫2 f (x) dx =1 – β .

x1

35

На практике обычно х1 и х2 выбирают так, что

Определенное таким образом практически предельное поле

рассеяния принимают за поле допуска, т. е. 2δт = х2 −х1 .

Введем обозначения: δт = (x2 − x1 )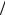2 − половина поля допуска;

т = (x1 + x2 )2 − координатасерединыполядопуска; αт = (Мx − т )/ δт − коэффициент относительной асимметрии; Kт = 3σδт − коэффици-

ент относительного рассеяния.

Индекс «Т» при , δ, α, K указывает на теоретическое значение этих коэффициентов, для эмпирических распределений эти коэффициенты будут иметь индекс «э».

В тех случаях, когда целью эксперимента является лишь определение или уточнение значений коэффициентов α и K относительно заданного конструктором поля допуска, не подлежащего пересмотру, коэффициенты αэ и Kэ определяются по формулам:

При этом может оказаться, что заданное конструктором поле допуска не соответствует практически предельному полю рассеяния, т. е. вероятность риска (брака) β ≠ 0,0027.

Практически предельное поле рассеяния оказывается не равным полю допуска даже в тех случаях, когда за величину поля допуска принимается вся зона рассеяния R.

1.5. Квантили распределения

Пусть Х – непрерывный количественный случайный признак с функцией распределения F(x) и плотностью распределения f(х). Квантилью порядка Р или Р-квантилью распределения F(x) называется величина xP, являющаяся решением уравнения

Поскольку для непрерывного признака ее функция распределения F(x) непрерывная и монотонно возрастающая, решение уравнения (1.20) – единственное (рис. 1.9).

36

F(x)

1

f (x)

P

–∞

где f(х) − плотность распределения.

Поэтому квантиль xР удовлетворяет соотношению x∫Р f (x) dx = Р.

–∞

На рис. 1.11 площадь под заштрихованной фигурой равна Р, а оставшаяся площадь под фигурой равна 1 − Р.

1.6. Интервальные оценки истинного значения

Рассмотренные ранее оценки результата измерения (x, S ), выраженного одним числом, называются точечными оценками.

Точечная оценка погрешности измерения не полная, поскольку S указывает на границы интервала, в котором может находиться

37

истинное значение x, но ничего не говорит о вероятности попадания x в этот интервал.

Более полным и надежным способом оценки случайных величин является определение интервальной оценки, которая с заданной степенью достоверности включает в себя значение оцениваемого параметра.

Вероятность того, что случайная погрешность не выйдет за пределы x1, x2, называется доверительным интервалом, а соответствующая ему вероятность появления случайной погрешности –

доверительной вероятностью α:

где хн = х – х1, хв = х + х2 – нижняя и верхняя доверительные границы параметра х; β – уровень значимости (β = Р(хн > х > хв) = 1– α).

Доверительная вероятность определяет область допустимых значений, а уровень значимости – критическую область, т.е. вероятность того, что х выйдет за пределы [x1, x2 ]. Выбираемое значение β должно быть достаточно малым, чтобы не была совершена ошибка первого рода, т. е. чтобы не была забракована правильная оценка. С другой стороны, слишком малое значение β может привести к ошибке второго рода, когда будет принята ложная оценка. Уровень значимости лежит в пределах 0,02 ≤ β ≤ 0,1.

Доверительный интервал характеризует степень воспроизводимости результатов измерений, причем при большом доверительном интервале наблюдается большая доверительная вероятность. Таким образом, доверительный интервал и доверительная вероятность – основные характеристики случайной погрешности.

Наиболее часто значения доверительных вероятностей принимают равными 0,90; 0,95; 0,99 или уровни значимости соответст-

венно 0,10; 0,05; 0,01.

Доверительный интервал обычно выражают через относительную величину α в долях среднеквадратической погрешности, т.е. α = ξ / σ. Например, при доверительном интервале ξ = σ доверительная вероятность α = 0,68. Это значит, что 68% случайных погрешностей не будут превышать значения σ. При ξ = 2σ α = 0,95, при ξ = 2,5σ α = 0,988, а при ξ = 3σ α = 0,997. В технических измерениях ограничиваются доверительной вероятностью α = 0,95.

38

При нормальном законе распределения случайных погрешностей часто пользуются доверительным интервалом от +3σ до –3σ, для которого доверительная вероятность равна 0,9973. Такая доверительная вероятность означает, что в среднем из 370 случайных погрешностей только одна по абсолютному значению будет больше 3σ.

Определение доверительных границ случайных погрешностей производится на основе вычисленного значения σ с учетом заданной доверительной вероятности и числа наблюдений N. При этом предполагается, что результаты наблюдений распределены по нормальному закону.

Доверительные границы х определяются по уравнениям:

где tα(N −1) − квантиль распределения Стьюдента для вероятности α

или уровня значимости β = 1 – α и числа степеней свободы f = N–1; величина tα(N −1) находится по табл. П1.

В случае двустороннего определения доверительных границ

39

1.7. Методы оценки точности результатов

При проектировании и изготовлении изделий различают следующие виды точности:

•τз − заданную (требуемую) точность − это точность, которую надо получить после изготовления изделия. Она задается конструктором в чертежах или технических условиях на изготовление на основании кинематических, геометрических, прочностных и других расчетов. В результате расчетов устанавливаются допустимые отклонения – допуск на изготовление;

•τд − действительная точность, т. е. точность, которая достигается при изготовлении и измерении;

•τω − расчетная − ожидаемая точность, т. е. точность, которая ожидается после обработки, согласно проектному технологическому процессу.

Существующие методы расчетов точности подразделяются на аналитические и опытно-статистические.

Аналитические методы требуют расчета всех составляющих погрешностей, порождаемых известными и неизвестными, зависимыми и независимыми факторами, и определения суммарной погрешности.

Основой этого метода расчета является использование теории размерных цепей, методов и правил определения частных погрешностей, принятых методов математического суммирования систематических постоянных и переменных погрешностей и случайных погрешностей.

Опытно-статистический метод требует проведения экспери-

ментальных работ. Основой этого метода является использование теории вероятности, математической статистики, методов построения точечных диаграмм и кривых практического распределения размеров (погрешностей).

1.8. Точечные диаграммы и практические кривые распределения размеров

Точечные диаграммы и кривые распределения размеров (погрешностей) позволяют управлять точностью технологических процессов и самими процессами изготовления изделий. На основании этих диаграмм можно организовывать различные методы статисти-

40