
Е. А. Ровба - Высшая математика
.pdf60 |
Глава 1. Линейная алгебра |
|
|
или нет. Ответ на этот вопрос может дать приводимый ниже общий критерий.
Теорема 1.6 (критерий Кронекера — Капелли). Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу ее расширенной матрицы:
¯
rank A = rank A = r.
Если при этом ранг r равен числу неизвестных n, то система имеет единственное решение. Если r < n, то система имеет бесконечное множество решений, определяемых n − r свободными неизвестными.
Д о к а з а т е л ь с т в о. В соответствии с рассуждениями при рассмотрении метода Гаусса система совместна в том и только в том случае, если в процессе исключения неизвестных не было получено ни одного уравнения с нулевыми коэффициентами и ненулевым свободным членом. Но, согласно свойствам ранга матрицы, это возможно тогда и только тогда, когда ранг основной матрицы системы совпадает с рангом ее расширенной матрицы. Для завершения доказательства достаточно вспомнить замечания 1.13 и 1.14. 
Применим критерий Кронекера — Капелли к однородным системам линейных уравнений.
Теорема 1.7. Однородная система линейных уравнений с n неизвестными и основной матрицей A имеет ненулевое решение тогда и только тогда, когда ранг основной матрицы меньше числа неизвестных, т.е. rank A < n.
Д о к а з а т е л ь с т в о. Необходимость. Пусть однородная система имеет ненулевое решение. Предположим от противного, что неравенство rank A < n неверно. Тогда rank A n. Но по свойству 1 ранга матрицы rank A n. Отсюда следует, что rank A = n. В этом случае, согласно критерию Кронекера — Капелли, система имеет единственное решение. Это решение может быть только нулевым, поскольку любая однородная система имеет нулевое решение. Полученный вывод приводит к противоречию.
Достаточность. Пусть rank A < n. Тогда на основании критерия Кронекера — Капелли система имеет бесконечно много решений, а значит, и хотя бы одно ненулевое. 

1.2. Системы линейных алгебраических уравнений |
61 |
|
|
Следствие 1.1. Если число уравнений однородной системы меньше числа ее неизвестных, то система имеет ненулевое решение.
Следствие 1.2. Если в однородной системе число уравнений равно числу неизвестных, то она имеет ненулевое решение тогда и только тогда, когда определитель основной матрицы системы равен нулю.
Д о к а з а т е л ь с т в о. Обозначим через n размер основной матрицы A системы, которая по условию является квадратной. Тогда очевидно, что строгое неравенство rank A < n равносильно равенству ну-
лю определителя матрицы A. |
11x1 + 3x2 + 8x3 − 2x4 = 0, |
||||
|
|||||
Пример 1.30. Решить систему |
7x1 |
+ 2x2 |
+ 3x3 |
+ 3x4 = 0, |
|
|
1 |
2 |
3 |
− |
4 |
|
|||||
|
4x |
+ x + 5x |
|
5x = 0. |
|
Р е ш е н и е. Данная система однородна, поэтому для ее решения будет достаточно привести с помощью элементарных преобразований строк к ступенчатому виду основную, а не расширенную матрицу
|
|
11 |
3 |
8 |
−2 |
A = |
4 |
1 |
5 |
5 |
|
|
|
|
|
|
− |
Это уже было сделано в задаче 1.25 при нахождении ранга матрицы A. Мы пришли к ступенчатому виду
−1 0 −7 13 . 4 1 5 −5
Отсюда находим:
x1 = −7x3 + 13x4,
x2 = −4x1 − 5x3 + 5x4 = −4(−7x3+13x4) − 5x3 + 5x4 = 23x3 − 47x4.
Переменные x3 и x4 свободные. Положив x3 = α, x4 = β, получим общее решение:
x1 = −7α + 13β, x2 = 23α − 47β, x3 = α, x4 = β, α, β R.
62 |
Глава 1. Линейная алгебра |
|
|
1.2.6. Экономическая модель Леонтьева
Предположим, что экономика страны насчитывает n отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного личного и общественного потребления, лежащего вне сферы материального производства. Рассмотрим процесс производства за некоторый период времени, например год.
Определение 1.48. Вектором валового выпуска назовем век- тор-столбец X = (xi), где xi — общий, или валовой, объем продукции i-й отрасли.
Определение 1.49. Вектором конечного продукта назовем вектор-столбец Y = (yi), где yi — объем конечного продукта i-й отрасли для непроизводственного потребления.
Определение 1.50. Матрицей прямых затрат назовем квадратную матрицу A = (aij ), где aij — коэффициенты прямых затрат, показывающие затраты продукции i-й отрасли на производство единицы продукции j-й отрасли.
Поскольку валовой объем продукции i-й отрасли равен суммарному объему ее продукции, потребляемой всеми отраслями, и конечного продукта, то
n |
|
j |
(1.16) |
xi = aij xj + yi, i = 1, 2, . . . , n. |
|
=1 |
|
Определение 1.51. Уравнения (1.16) называются соотношениями баланса и задают модель Леонтьева многоотраслевой экономики.
Перепишем соотношения баланса (1.16) в виде системы линейных уравнений:
|
− (a11x1 |
+ a12x2 |
+ . . . + a1nxn) = y1, |
x1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
− (a21x1 |
+ a22x2 |
+ . . . + a2nxn) = y2, |
x2 |
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
xn − (an1x1 + an2x2 + . . . + annxn) = yn.
1.2. Системы линейных алгебраических уравнений |
63 |
|
|
Полученную систему преобразуем к матричному виду: |
|
X − AX = Y, EX − AX = Y, (E − A)X = Y, |
(1.17) |
где E — единичная матрица.
Основная задача межотраслевого баланса состоит в отыскании такого валового объема продукции для каждой из отраслей, который при известных прямых затратах обеспечивает заданный конечный продукт.
Из экономического смысла матрицы A и вектора Y следует, что все их элементы неотрицательны. В данном подпараграфе мы будем называть такие матрицы неотрицательными, а матрицы со строго положительными элементами — положительными. Очевидно, что вектор неизвестных X также должен быть неотрицательным. Сформулируем условия, обеспечивающие выполнение этого требования.
Определение 1.52. Неотрицательная матрица A называется продуктивной, если для любого неотрицательного вектора Y существует неотрицательное решение X системы (1.17). В этом случае и модель Леонтьева, определяемая матрицей A, также называется продуктивной.
Существует несколько критериев продуктивности матрицы прямых затрат. Приведем некоторые из них.
Теорема 1.8 (первый критерий продуктивности). Если матрица A неотрицательна и для некоторого положительного вектора Y система (1.17) имеет неотрицательное решение X, то матрица A продуктивна.
Из соотношения (1.17) в случае существования обратной матрицы (E − A)−1 следует, что
X = (E − A)−1Y.
Матрица (E − A)−1 называется матрицей полных затрат. Следующая теорема дает более эффективное условие продуктив-
ности.
Теорема 1.9 (второй критерий продуктивности). Неотрицательная матрица A продуктивна тогда и только тогда, когда матрица (E − A)−1 существует и неотрицательна.

64 Глава 1. Линейная алгебра
Теорема 1.10 (третий критерий продуктивности). Неотрицательная матрица A продуктивна, если сумма элементов любого ее столбца или любой строки меньше единицы.
Пример 1.31. Определить вектор X валового выпуска продукции трех отраслей, если известны матрица прямых затрат A и вектор
конечного продукта Y : |
|
|
|
|
|
|
|
0,08 0,10 |
0,14 |
|
|
510 |
|
A = |
0,03 |
0,04 |
0,09 , |
Y = |
405 . |
|
|
|
|
|
|
|
|
|
0,06 |
0,08 |
0,06 |
|
482 |
|
Р е ш е н и е. Сразу отметим, что, согласно третьему критерию продуктивности, матрица A является продуктивной. Будем приводить к ступенчатому виду расширенную матрицу (E − A|Y ) системы (1.17):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
46 |
|
|
−5 |
−7 |
|
|
25 500 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
0,92 |
|
0,10 |
|
|
0,14 |
|
510 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
− |
|
− |
|
|
|
|
−0,09 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
0,03 |
−0,96 |
|
|
405 |
|
, |
|
|
1 |
|
|
32 |
− |
3 |
|
|
13 500 , |
||||||||||||||||
|
|
|
−0,06 |
|
0,08 |
|
−0,94 |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
482 |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
4 |
47 |
|
|
24 100 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
1467 |
|
|
145 |
|
646 500 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
32 |
|
− −3 |
|
|
|
13 500 . |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
100 |
|
|
56 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
−0 |
|
|
|
|
|
|
|
|
16 400 |
|
|
|
|
|
|
|
|||||||||||
|
|
Домножим первую строку матрицы на 100, чтобы сделать второй |
||||||||||||||||||||||||||||||||||
ее элемент кратным выбранному разрешающему элементу: |
|
|||||||||||||||||||||||||||||||||||
|
0 |
|
146700 |
− |
14 500 |
|
|
|
|
0 |
|
|
|
0 |
67652 |
|
|
|||||||||||||||||||
|
|
64 650 000 |
|
|
|
|
|
591 200 |
||||||||||||||||||||||||||||
1 |
|
|
|
32 |
|
− |
3 |
|
|
|
|
13 500 , |
1 |
|
|
|
32 |
|
− |
3 |
|
40 |
13 500 . |
|||||||||||||
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
− |
|
||||||
|
0 |
|
|
|
100 |
|
|
|
|
56 |
|
|
|
|
16 400 |
−0 |
|
|
|
100 |
|
56 |
|
|
16 400 |
|||||||||||
Отсюда получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
56x3 + 16 400 |
|
|
x1 = 32x2 − 3x3 − 13 500 = 700. |
|||||||||||||||||||||||||
x3 = 600, x2 = |
|
|
|
|
|
|
|
= 500, |
||||||||||||||||||||||||||||
|
|
|
100 |
|
|
|
||||||||||||||||||||||||||||||
Итак, чтобы обеспечить конечный продукт Y , необходимо выпустить 700 единиц продукции первой отрасли, 500 — второй и 600 — третьей отрасли. 
1.3. Векторная алгебра |
65 |
|
|
1.3. Векторная алгебра
1.3.1. Векторы в пространстве
Многие величины, например сила и скорость, определяются не только своим числовым значением, но и направлением. Такие величины называются векторными.
−−→
Определение 1.53. Вектором AB называется направленный отрезок с началом в точке A и концом в точке B. Определенный таким образом вектор называют еще связанным.
Определение 1.54. Длиной или модулем вектора называется
−−→
длина соответствующего направленного отрезка. Длина вектора AB
−−→
обозначается |AB|.
Определение 1.55. Вектор, начало и конец которого совпадают, называется нулевым и обозначается 0.
Определение 1.56. Вектор, длина которого равна единице, называется единичным вектором или ортом и обозначается e.
Определение 1.57. Два ненулевых вектора называются кол-
линеарными, если они лежат на одной прямой или на параллельных
−−→ −−→
прямых. Коллинеарные векторы AB и CD могут быть одинаково на-
правлены (сонаправлены), если их концы лежат в одной полуплоскости от прямой, проходящей через их начала, или, в противном слу-
чае, противоположно направлены. Это обозначается соответственно |
||||
−−→ |
−−→ |
−−→ |
↓↑ |
−−→ |
AB |
CD |
или AB |
|
CD. |
Определение 1.58. Два вектора называются равными, если они имеют равные длины и сонаправлены.
Определение 1.59. Свободным вектором или параллельным переносом называется совокупность равных между собой векторов.
Для обозначения свободных векторов применяются строчные буквы латинского алфавита, например a.
Определение 1.60. Углом между векторами называется наименьший угол, на который надо повернуть один из векторов, чтобы его направление совпадало с направлением другого вектора. Для угла ϕ между векторами a и b вводится обозначение ϕ = (a, b).
66 |
Глава 1. Линейная алгебра |
|
|
Ясно, что для всякого угла ϕ между векторами верно двойное неравенство 0 ϕ π.
Определение 1.61. Если (a, b) = π/2, то говорят, что векторы a и b ортогональны, и пишут a b.
Определение 1.62. Произведением вектора a и числа k называется вектор b = ka, длина которого |b| = |k||a| и направление совпадает с направлением вектора a, если k > 0, и противоположно ему, если k < 0 (рис. 1.4).
Замечание 1.18. Из определения 1.62 следует, что ненулевые векторы a и b коллинеарны тогда и только тогда, когда для некоторого числа k верно равенство b = ka, причем при k > 0 векторы a и b сонаправлены, при k < 0 — противоположно направлены.
a
2a
a
−3a
Рис. 1.4
b
b a+
Рис. 1.5
a
b a+
b
Рис. 1.6
Определение 1.63. Противоположным вектором −a называется произведение вектора a и числа −1, т.е. −a = (−1)a.
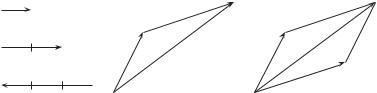
Определение 1.64. Пусть a и b — любые два вектора. Поместим начало вектора b в конец вектора a. Вектор, соединяющий начало вектора a с концом вектора b, назовем суммой векторов a и b и будем обозначать a + b. Это правило сложения векторов называют правилом треугольника (рис. 1.5).
Сумму двух векторов можно построить также по правилу параллелограмма (рис. 1.6). Сложить несколько векторов можно по правилу ломаной, которое является обобщением правила треугольника (рис. 1.7).

1.3. Векторная алгебра |
|
67 |
|
|
|
b |
|
|
|
c |
a − b |
a |
|
a |
a + b + |
c |
|
|
b |
|
|
|
|
Рис. 1.7 |
Рис. 1.8 |
|
Определение 1.65. Разностью двух векторов a и b называется сумма вектора a и вектора −b, противоположного b (рис. 1.8).
Определение 1.66. Линейными операциями над векторами
называются операции сложения и вычитания векторов и операция умножения вектора на число.
1.3.2. Алгебраическое описание вектора
Для алгебраического описания векторов их связывают с некоторой прямоугольной декартовой системой координат.
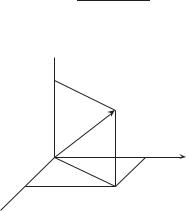
Определение 1.67. Пусть a — произвольный вектор на плоско-
−−→
сти. Рассмотрим равный ему вектор OM с началом в начале выбран-
ной прямоугольной декартовой системы координат. Тогда конец векто-
−−→
ра OM однозначно определит некоторую точку M плоскости, координаты x, y которой будем называть координатами вектора a (рис. 1.9).
y |
|
M(x, y) |
|
|
|
|
|
||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
x |
x |
|
|
|
Рис. 1.9 |
|
|
|
|
|
|
|
Наоборот, задав произвольную точку плоскости M(x, y), мы тем
−−→
самым определим вектор a = OM (рис. 1.9).
68 |
Глава 1. Линейная алгебра |
|
|
Аналогично устанавливается взаимно однозначное соответствие векторов и точек пространства. В этом случае координатами вектора a считаются координаты x, y, z соответствующей точки M пространства. В дальнейшем сосредоточимся на рассмотрении пространственного случая.
Замечание 1.19. Мы установили взаимно однозначное соответствие точек трехмерного пространства или плоскости и векторов. Это позволяет полностью отвлечься от геометрического смысла векторов и иметь дело лишь с координатами.
Согласно теореме Пифагора длина вектора a с координатами x, y, z (рис. 1.10) может быть найдена по формуле
! |
|
|a| = x2 + y2 + z2. |
(1.18) |
z 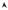
z
M(x, y, z)
a
y
O
y
x
 x
x
Рис. 1.10
Линейные операции над векторами сводятся к соответствующим линейным операциям над их координатами, а именно — верна следующая теорема.
Теорема 1.11. Если a = (x1, y1, z1), b = (x2, y2, z2) и k —
число, то
ka = (kx1, ky1, kz1), a + b = (x1 + x2, y1 + y2, z1 + z2). (1.19)

1.3. Векторная алгебра |
|
|
|
|
|
|
|
|
|
|
|
|
69 |
|||
|
|
|
||||||||||||||
Если даны две точки: M1(x1, y1, z1) и M2(x2, y2, z2), то вектор с |
||||||||||||||||
началом в точке M1 и концом в точке M2 |
|
|
|
|
|
|
|
|||||||||
−−−−→ |
−−−→ |
−−−→ |
= (x , y |
, z |
) |
|
(x , y |
, z |
) = |
|
|
|||||
M |
M |
2 |
= OM |
2 − |
OM |
1 |
− |
|
|
|||||||
1 |
|
|
|
2 2 |
2 |
|
1 1 |
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
= (x2 − x1, y2 − y1, z2 − z1). |
|
|||||||
Расстояние M1M2 |
между точками M1(x, y, z) и M2(x, y, z) про- |
|||||||||||||||
странства равно длине вектора |
−−−1 −→2 |
|
|
|
|
|
|
|
|
|||||||
M M : |
|
|
|
|
|
|
|
|
||||||||
M1M2 = |−−−1 −→2| |
! |
|
|
|
|
|
||||||||||
(x2 − x1) + (y2 − y1) |
+ (z2 |
− z1) . |
|
|||||||||||||
|
M M = |
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
(1.20) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Теорема 1.12. Ненулевые векторы a = (x1, y1, z1) и b = = (x2, y2, z2) коллинеарны тогда и только тогда, когда их координаты
пропорциональны:
x1 = y1 = z1 . x2 y2 z2
Д о к а з а т е л ь с т в о. Согласно замечанию 1.18 векторы a и b коллинеарны тогда и только тогда, когда для некоторого числа k верно равенство a = kb. По теореме 1.11 это равносильно покоординатным равенствам x1 = kx2, y1 = ky2, z1 = kz2, которые могут быть
переписаны в виде
x1 = y1 = z1 = k. x2 y2 z2
Все перечисленные выше результаты верны и для векторов на плоскости. Например, расстояние между точками M1(x, y) и M2(x, y) может быть вычислено по формуле
!
M1M2 = (x2 − x1)2 + (y2 − y1)2. |
(1.21) |
1.3.3. Скалярное произведение векторов
Определение 1.68. Скалярным произведением двух векторов
называется число (скаляр), равное произведению длин этих векторов и косинуса угла между ними. Скалярное произведение векторов a и b обозначается a · b или просто ab. Итак,
a · b = |a||b| cos(a, b). |
(1.22) |
