
Е. А. Ровба - Высшая математика
.pdf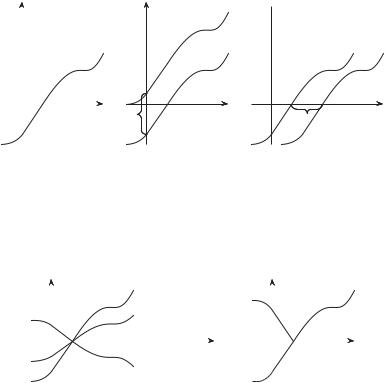
150 |
Глава 3. Предел последовательности и функции |
|
|
3.2.6. Построение графиков функций
Зная графики основных элементарных функций, научимся строить графики более сложных функций с помощью линейных преобразований.
Пусть задана функция y = f(x) и ее график известен (рис. 3.33). График функции y = f(x) + c получается из графика функции y = f(x) с помощью параллельного переноса последнего вдоль оси Oy
на величину, равную c (рис. 3.34).
График функции y = f(x − a) получается из графика функции y = f(x) с помощью сдвига последнего вдоль оси Ox на величину, равную a (рис. 3.35).
y |
|
y = f(x) |
|
|
|||
|
|
||
|
|
|
|
O |
|
x |
|
|
|
Рис. 3.33 |
|
|
|
||
yy = f(x)+c
c O |
x |
y = f(x) |
|
Рис. 3.34 |
|
y 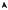
y = f(x)
O |
a |
x |
y = f(x − a)
Рис. 3.35
График функции y = kf(x), где k > 0, получается из графика функции y = f(x) растяжением в k раз вдоль оси Oy (при k < 1 — сжатием). Если k < 0, то график функции y = kf(x) получается из графика функции y = −kf(x) зеркальным отображением относительно оси Ox (рис. 3.36).
y |
|
y = f(x) |
|
|
y |
|
y = |f(x)| |
|||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||
|
|
y = |
1 |
f(x) |
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
1 |
|
x |
O |
|
x |
||||
|
|
|
|
|
|
|
|
y = f(x) |
||||
|
|
y = − |
|
f(x) |
|
|
||||||
|
|
2 |
|
|
|
|
||||||
Рис. 3.36 |
Рис. 3.37 |

3.2. Функциональная зависимость |
151 |
|
|
График функции y = f(kx), где k > 0, получается из графика функции y = f(x) растяжением (при 0 < k < 1) или сжатием (при k > 1) вдоль оси Ox. При k < 0 нужно зеркально отобразить график функции y = f(−kx) относительно оси Oy.
Остановимся еще на одном часто встречающемся преобразовании графиков функций. Чтобы получить график функции y = |f(x)|, нужно участки графика функции y = f(x), лежащие выше оси Ox, оставить без изменений, а участки графика, лежащие ниже оси Ox, зеркально отобразить относительно этой оси (рис. 3.37).
Пример 3.31. Построить график функции y = |1 + (x − 1)3|.
Р е ш е н и е. В качестве исходного возьмем график функции y = x3 (рис. 3.38). Путем сдвига на 1 ед. вправо вдоль оси Ox получим график функции y = (x − 1)3 (рис. 3.39).
|
y |
|
|
|
|
y = x3 |
|
|
y |
|
y = (x − 1)3 |
||
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
O |
|
||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
1 |
x |
−1 |
|
1 |
x |
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.38 |
|
|
|
|
Рис. 3.39 |
|
|
||||
Если перенести этот график вдоль оси Oy на 1 ед. вверх, то |
|||||||||||||
получим график функции |
y |
= 1 + (x − 1)3 (рис. |
3.40). Наконец, |
||||||||||
зеркально отобразив часть графика, расположенную ниже оси Ox, получим график функции y = |1 + (x − 1)3| (рис. 3.41). 
y |
|
|
|
|
y = 1 + (x − 1) |
y |
|
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
y = |1 + (x − 1)3| |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
O |
1 |
x |
O |
|
1 |
x |
||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.40 |
Рис. 3.41 |

152 |
Глава 3. Предел последовательности и функции |
|
|
3.2.7.Функциональная зависимость в экономике
Применение математического аппарата в экономических исследованиях способно принести большую пользу. Но прежде чем применить математические методы, исследователь должен составить математическую модель прикладной задачи. Такой математической моделью может, например, стать описание какого-либо экономического процесса в виде математической функции. Рассмотрим важнейшие функциональные зависимости, используемые в экономике.
Определение 3.32. Функция издержек C = C(q) выражает зависимость издержек производства C от объема выпуска q.
Пример 3.32. Если функция издержек некоторого производства
задается формулой C = 100√q, то при объеме выпуска 25 ед. издержки
√
C = 100 25 = 500 ден. ед.
Определение 3.33. Функция выручки R = R(q) задает зависимость выручки R от объема выпуска q.
Пример 3.33. Если продано q единиц товара по цене p за каждую единицу, то выручка R = pq.
Определение 3.34. Функция прибыли P = P (q) — это зависимость прибыли P от объема выпуска q.
Прибыль равна разности выручки и издержек:
P (q) = R(q) − C(q).
Определение 3.35. Точка безубыточности — это такой объем выпуска q, при котором издержки равны выручке: C(q) = R(q).
Очевидно, что при достижении объемом выпуска точки безубыточности прибыль становится равной нулю.
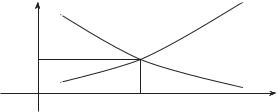
Определение 3.36. Функции спроса и предложения D = D(p) и
S = S(p) задают зависимость спроса и предложения от цены товара p (рис. 3.42).
Естественно, что по мере увеличения цены предложение растет, а спрос падает.
3.3. Предел функции. Два замечательных предела |
153 |
|
|
y
S
Q0
D
O |
p0 |
x |
Рис. 3.42
Определение 3.37. Точка рыночного равновесия (p0, Q0) — это точка пересечения линий спроса и предложения (рис. 3.42). При этом цена p0 называется равновесной ценой, а объем продаж Q0 —
равновесным объемом продаж.
Определение 3.38. Производственная функция выражает зависимость результатов производства от обусловливающих его факторов.
Определение 3.39. Функция полезности u(x) дает субъективную числовую оценку полезности некоторого действия.
3.3.Предел функции.
Два замечательных предела
3.3.1. Предел функции по Гейне
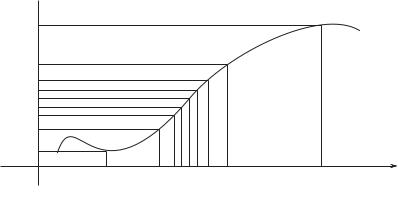
Определение 3.40. Пусть функция f определена в некоторой окрестности точки x = a, за исключением, быть может, самой точки a. Возьмем последовательность точек {xn} из этой окрестности, сходящуюся к точке a. Значения функции в точках последовательности, в свою очередь, образуют последовательность f(x1), f(x2), . . . , f(xn), . . .
(рис. 3.43).
Число b называется пределом функции f в точке x = a (или при x → a), если для любой последовательности {xn}, сходящейся к a и такой, что xn = a для всех n N, соответствующая последовательность значений функции {f(xn)} сходится к b.
154 |
Глава 3. Предел последовательности и функции |
|
|
y 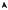
f(x2)
y = f(x)
f(x4)
|
|
|
|
b |
|
|
|
|
|
f(x3) f(x1)
|
|
|
|
|
|
|
|
O |
x1 |
x3 |
|
a |
x4 |
x2 |
x |
Рис. 3.43
Другими словами, число b называется пределом функции f в
точке x = a, если
{xn} |
, x |
= a (n |
|
N), |
lim x |
|
= a, |
lim f(x ) = b. |
|
|
n |
|
n→∞ |
n |
|
n→∞ |
n |
||
Данное определение называется определением предела функции по Гейне или на языке последовательностей.
Предел функции f в точке x = a обозначается следующим образом:
lim f(x) = b.
x→a
Определение 3.41. Число b называется пределом функции f
при x → ∞ (или на бесконечности), если для любой ББП {xn} соответствующая последовательность значений функции {f(xn)} сходится к b. Для обозначения предела функции на бесконечности применяется запись
lim f(x) = b.
x→∞
Пример 3.34. Постоянная функция f(x) = C в каждой точке имеет предел. Действительно, пусть a R и {xn} — произвольная последовательность, сходящаяся к a. Тогда для всякого n N верно, что f(xn) = C. В этом случае последовательность {f(xn)} будет иметь своим пределом число C.
3.3. Предел функции. Два замечательных предела |
155 |
|
|
Пример 3.35. Функция
π
x
определена всюду на R, за исключением точки x = 0 (рис. 3.44). Выясним, существует ли предел этой функции в точке x = 0. С этой целью рассмотрим две последовательности.
y |
π |
y = sin |
|
1 |
x |
O |
x1 y2 |
y1 |
x0 |
x |
−1
Рис. 3.44
Пусть первую последовательность составляют числа xn > 0 такие, что sin(π/xn) = 1, т.е. xn = 2/(4n + 1), n N. Очевидно, что последовательность {xn} сходится к точке x = 0, а соответствующая последовательность значений функции будет состоять из единиц и иметь своим пределом число 1.
Теперь возьмем другую последовательность значений аргумента
{yn}, где yn > 0 и n N, такую, что sin(π/yn) = 0, т.е. yn = 1/n, n N. Очевидно, что в этом случае последовательность значений ар-
гумента {yn} сходится к нулю, а соответствующая последовательность значения функции {sin(π/yn)} также сходится к нулю.
Таким образом, в первом случае последовательность значений функции сходится к 1, а во втором — к 0. Это означает, что у функции f(x) = sin(π/x) в точке x = 0 предел не существует. Данный факт иллюстрируется графиком рассматриваемой функции (рис. 3.44).
3.3.2. Предел функции по Коши
Дадим теперь определение предела функции по Коши, эквивалентное рассмотренному выше определению по Гейне. Два определе-
156 |
Глава 3. Предел последовательности и функции |
|
|
ния или более принято называть эквивалентными, если выполнение любого из них влечет выполнение любого другого.
Определение 3.42. Число b называется пределом функции f
в точке x = a, если для любого числа ε > 0 существует положительное число δ такое, что для всякого x, удовлетворяющего условию 0 < |x − a| < δ, выполняется неравенство |f(x) − b| < ε.
Другими словами, число b называется пределом функции f в
точке x = a, если
ε > 0 δ > 0 x, 0 < |x − a| < δ, |f(x) − b| < ε.
Данное определение называется определением предела функции по Коши или на языке ε — δ.
Заметим, что число δ, δ > 0, зависит от выбора числа ε, ε > 0. Доказательство эквивалентности определений предела функции
по Гейне и по Коши мы опустим.
Определение предела функции по Коши можно переформулировать в следующем виде.
Определение 3.43. Число b называется пределом функции f в
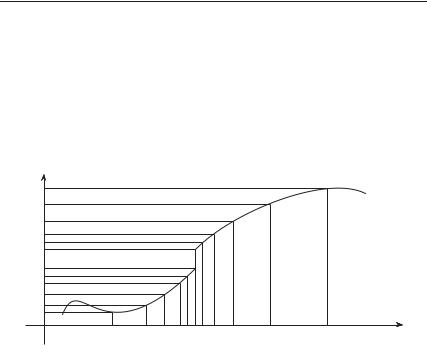
точке x = a, если для любой ε-окрестности точки b найдется такая δ-окрестность точки a, что для всех x = a из этой δ-окрестности соответствующие значения функции f(x) лежат в ε-окрестности точки b.
y |
|
|
|
y = f(x) |
|
|
|
|
|
b + ε |
|
|
|
|
b |
|
|
|
|
b − ε |
|
|
|
|
O |
a − δ |
a |
a + δ |
x |
|
|
|
||
|
|
Рис. 3.45 |
|
|
Определение 3.43 называется определением предела функции на языке окрестностей и выражает геометрический смысл предела функции (рис. 3.45).
3.3. Предел функции. Два замечательных предела |
|
157 |
|||||
3.3.3. Односторонние пределы |
|
|
|||||
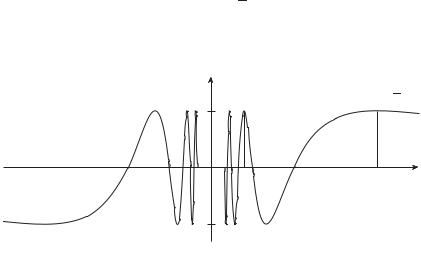
Определение 3.44. Число c называется правым пределом функ- |
|||||||
ции f в точке x = a, если для любой сходящейся к a последователь- |
|||||||
ности {yn}, члены которой больше a, соответствующая последователь- |
|||||||
ность {f(yn)} сходится к c (рис. 3.46). Символически это записывается |
|||||||
следующим образом: |
|
|
|
|
|
|
|
|
|
|
lim |
f(x) = c. |
|
|
|
|
|
x→a+0 |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = f(x) |
c |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
O |
x1 |
x2 x3 |
a |
y3 |
y2 |
y1 |
x |
|
|
|
Рис. 3.46 |
|
|
|
|
Аналогично определяется левый предел.
Определение 3.45. Число b называется левым пределом функции f в точке x = a, если (рис. 3.46)
x |
, x < a (n |
|
N), |
lim x |
|
= a, |
lim f(x ) = b. |
|
{ n} |
n |
|
n→∞ |
n |
|
n→∞ |
n |
|
В этом случае применяется обозначение |
lim |
f(x) = b. |
||||||
|
|
|
|
|
|
x→a−0 |
|
|
Если a = 0, то используются следующие обозначения:
lim f(x), lim f(x).
x→+0 x→−0
Определение 3.46. Правый и левый пределы функции в точке называются односторонними.
158 |
Глава 3. Предел последовательности и функции |
|
|
Определение 3.47. Число b называется пределом функции f
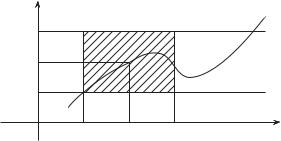
при x → +∞, если для любой такой ББП {xn}, что xn > 0 для всех n N, соответствующая последовательность {f(xn)} сходится к b.
Аналогично определяется предел функции при x → −∞. Для записи таких пределов применяются обозначения:
lim f(x) = b, |
lim f(x) = b. |
x→+∞ |
x→−∞ |
Сформулируем определения односторонних пределов на языке
ε — δ. Число b называется правым (левым) пределом функции f в точке x = a, если
ε > 0 δ > 0 x, a < x < a + δ (a − δ < x < a), |f(x) − b| < ε.
Пример 3.36. Функция y = sign x (см. рис. 3.6) имеет односторонние пределы в точке x = 0. Очевидно, что
lim sign x = 1, |
lim sign x = |
− |
1. |
x→+0 |
x→−0 |
|
Следующая теорема устанавливает связь между односторонними пределами и пределом функции.
Теорема 3.7. Для того чтобы функция f имела предел в точке x = a, необходимо и достаточно, чтобы существовали и были равны односторонние пределы. В этом случае предел функции равен односторонним пределам:
lim f(x) = |
lim f(x) = |
lim f(x). |
x→a |
x→a−0 |
x→a+0 |
3.3.4. Бесконечно малые функции
Определение 3.48. Функция α(x) называется бесконечно малой при x → a (БМФ), если
lim α(x) = 0.
x→a
Согласно определению предела функции по Коши функция α(x) является бесконечно малой при x → a тогда и только тогда, когда
ε > 0 δ > 0 x, 0 < |x − a| < δ, |α(x)| < ε.

3.3. Предел функции. Два замечательных предела |
159 |
|
|
Замечание 3.6. Обратим внимание на необходимость указания точки, в которой функция является бесконечно малой. Например, функция y = x2 является бесконечно малой при x → 0, но не является бесконечно малой при x → 1. В самом деле,
lim x2 = 0, |
lim x2 = 1. |
x→0 |
x→1 |
Свойства БМФ
1.Сумма любого конечного числа БМФ есть БМФ.
До к а з а т е л ь с т в о. Достаточно доказать это свойство для суммы двух БМФ. Пусть α(x) и β(x) — БМФ при x → a. Докажем, что α(x) + β(x) — тоже БМФ при x → a.
Зададимся произвольным числом ε > 0. Так как α(x) — БМФ при x → a, то
δ1 > 0 |
x, 0 < |x − a| < δ1, |
|α(x)| < |
|
ε |
||
|
|
|
. |
|||
2 |
||||||
Аналогично для β(x) |
|
|
|
|
|
|
δ2 > 0 |
x, 0 < |x − a| < δ2, |
|β(x)| < |
|
ε |
||
|
. |
|||||
2 |
||||||
Положим δ = min{δ1, δ2}. Тогда для всякого x, удовлетворяющего условию 0 < |x − a| < δ, выполняются оба условия: 0 < |x − a| < δ1 и 0 < |x − a| < δ2, поэтому
|
|
|
|
ε |
|
ε |
||
α(x) + β(x) |
|α(x)| + |β(x)| < |
|
+ |
|
= ε. |
|||
2 |
2 |
|||||||
Итак, мы |
доказали, что |
|
|
|
||||
ε > 0 δ > 0 x, 0 < |x − a| < δ, |
||||||||
|
|
|||||||
α(x) + β(x) < ε. |
||||||||
Это означает, что сумма α(x) + β(x) является БМФ при x → a.
2. Бесконечно малая функция при x → a является ограниченной в некоторой окрестности точки a.
