
Е. А. Ровба - Высшая математика
.pdf
190 Глава 4. Дифференциальное исчисление
4.1.2. Геометрический смысл производной
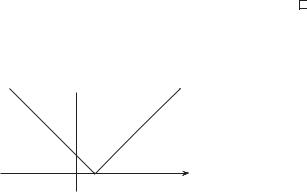
Пусть функция y = f(x) определена на интервале (a, b). Предположим, что кривая AB является графиком этой функции (рис. 4.1). Пусть M(x0, f(x0)) — какая-либо точка графика. Придадим аргументу приращение x в точке x0. Соответствующую точку на графике
обозначим P (x0 + |
x, f(x0 + |
x)). |
||||
|
|
y |
|
|
B |
|
|
|
|
||||
|
|
|
|
|
||
|
f(x0 + |
x) |
|
|
P |
|
|
|
|
|
|
||
|
|
|
|
|
T |
|
|
|
|
|
|
M |
|
|
f(x0) |
|
A |
N |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
a |
x0 x0 + x b x |
|
|
|
|
|
|
Рис. 4.1 |
|
Через точки M и P проведем прямую и назовем ее секущей. Если точку P устремить по кривой AB к точке M, то положение секущей будет, вообще говоря, изменяться.
Определение 4.2. Касательной к кривой в точке M называется предельное положение (если оно существует) секущей MP , когда точка P неограниченно приближается к точке M.
Обозначим через α угол между касательной MT и осью Ox (или, что то же самое, между касательной MT и прямой MN, рис. 4.1), а через ϕ — угол между секущей MP и осью Ox, т.е. α — угол наклона касательной MT к оси Ox, а ϕ — угол наклона секущей MP к оси Ox. Очевидно, что
lim tg ϕ = tg α.
P →M
Поскольку tg ϕ = MNPN , то будем иметь:
lim |
NP |
= tg α. |
|
||
P →M MN |
|
|

4.1. Производная функции |
|
191 |
|
|
|
|
|
Но из рис. 4.1 видно, что |
|
|
|
NP = f(x0 + x) − f(x0), MN = (x0 + x) − x0 = x. |
|||
Следовательно, |
|
|
|
lim |
f(x0 + |
x) − f(x0) |
= tg α, |
|
|||
|
x |
||
x→0 |
|
||
или f (x0) = tg α.
Геометрический смысл производной состоит в том, что производная функции y = f(x) в точке x = x0 есть тангенс угла наклона касательной к ее графику в точке (x0, f(x0)). Другими словами, f (x0) — это угловой коэффициент касательной к графику функции в точке
M(x0, y0).
Теперь, учитывая уравнение прямой, проходящей через данную точку с данным угловым коэффициентом (2.5), несложно получить
уравнение касательной: |
|
y − y0 = f (x0)(x − x0). |
(4.2) |
Прямая, проходящая через точку (x0, f(x0)) и перпендикулярная касательной, называется нормалью к графику в этой точке.
Учитывая условие перпендикулярности двух прямых (2.12), можем записать уравнение нормали:
y |
− |
y |
|
= |
−1 |
(x |
− |
x |
) |
(4.3) |
|
|
0 |
|
f (x0) |
|
0 |
|
|
при условии f (x0) = 0. Если же f (x0) = 0, то нормалью будет прямая x = x0.
Пример 4.3. Найти уравнение касательной и нормали к графику функции y = 2x + 3x−2 в точке (1, 5).
Р е ш е н и е. Полагаем x0 = 1. Очевидно, что y(1) = 5. Найдем угловой коэффициент касательной:
y = 2 − 6x−3, y (1) = 2 − 6 = −4.
192 |
Глава 4. Дифференциальное исчисление |
|
|
Теперь воспользуемся формулой (4.2) и запишем уравнение касательной в точке (1, 5):
y − 5 = (−4)(x − 1), y − 5 = −4x + 4, y = −4x + 9.
Уравнение нормали будет иметь следующий вид:
y − 5 = |
1 |
(x − 1), y = |
1 |
x + 4,75. |
|
|
|||
4 |
4 |
Следствие 4.1. Вернемся к примеру 4.2. Построим график функции y = |x − 1| (рис. 4.2).
y 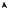
O 1 |
x |
Рис. 4.2 |
|
Очевидно, что график этой функции не имеет касательной в точке x = 1 и, следовательно, производной.
4.1.3. Физический смысл производной
Пусть некоторая материальная точка M движется прямолинейно и задан закон ее движения s = s(t), т.е. известно расстояние s(t) от точки M до некоторой начальной точки отсчета в каждый момент времени t. К моменту времени t0 точка пройдет расстояние s(t0), а к моменту времени t0 + t — расстояние s(t0 + t). За промежуток времени t точка M пройдет расстояние s = s(t0 + t) − s(t0).
Отношение s/ t можно рассматривать как среднюю скорость движения на промежутке времени [t0, t0 + t]. Чем меньше промежуток времени t, тем точнее соответствующая средняя скорость будет характеризовать движение точки в момент времени t0. Вследствие

4.1. Производная функции |
193 |
|
|
этого предел средней скорости движения при |
t → 0 называют ско- |
ростью (или мгновенной скоростью) движения точки M в момент |
|
времени t0 и обозначают v(t0), т.е. |
|
|
|
v(t0) = lim |
s(t0 + |
t) − s(t0) |
. |
|
|||
t→0 |
t |
||
Но выражение справа есть s (t0). Таким образом, v(t0) = s (t0), |
|||
т.е. скорость движения в момент времени t0 есть производная от пройденного расстояния по времени.
Понятие скорости, заимствованное из механики, удобно использовать и при изучении производной функции. Какую бы зависимость ни отражала функция y = f(x), отношение y/ x есть средняя скорость изменения зависимой переменной y относительно аргумента x на заданном промежутке, a y (x) есть скорость изменения y в точке x.
4.1.4. Правила дифференцирования
Теорема 4.2. Если функции u = u(x), v = v(x) в точке x имеют производные, то сумма, разность, произведение и частное этих функций также имеют производную в этой точке (частное при условии, что v(x) = 0) и справедливы следующие формулы:
1 v
|
(u ± v) = u ± v , |
(4.4) |
|||||||||
|
(uv) = u v + v u, |
(4.5) |
|||||||||
= |
|
v |
, |
|
u |
|
|
= |
u v − v u |
. |
(4.6) |
|
|
v |
|
|
|||||||
|
− v2 |
|
|
v2 |
|
||||||
Д о к а з а т е л ь с т в о. Сначала покажем, что (u + v) = u + v .
Воспользуемся определением производной: |
|
|
|
|
|
||||||||||
(u + v) = |
lim |
|
(u(x + x) + v(x + |
x)) − (u(x) + v(x)) |
= |
|
|||||||||
|
|
|
|
|
|
|
|||||||||
= |
x→0 |
|
|
x − |
|
|
x |
x |
− |
= |
|
||||
x→0 |
|
|
+ |
|
|
||||||||||
|
lim |
|
|
u(x + x) |
u(x) |
|
v(x + x) |
v(x) |
|
||||||
|
|
u(x + |
x) − u(x) |
+ |
lim |
v(x + |
x) − v(x) |
|
= u + v . |
||||||
= |
lim |
|
|
||||||||||||
|
|
|
|
||||||||||||
|
x→0 |
|
|
|
x |
|
|
x→0 |
|
|
x |
|
|||

194 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Глава 4. Дифференциальное исчисление |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Аналогично |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(u |
− |
v) = |
lim |
|
(u(x + x) − v(x + |
|
x)) − (u(x) − v(x)) |
= |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
= |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
lim |
u(x + x) u(x) |
|
|
|
v(x + x) v(x) |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
= |
|
|
|
|
|
x − |
|
|
|
|
− |
|
|
|
|
|
x − |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
= |
lim |
|
u(x + |
x) − u(x) |
|
− |
lim |
v(x + |
x) − v(x) |
|
= u |
− |
v . |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
x→0 |
|
|
|
|
|
|
x |
|
|
|
|
|
x→0 |
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||||||||
|
Для вывода формулы нахождения производной произведения |
||||||||||||||||||||||||||||||||||||||||||
поступим следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
(uv) = |
lim |
|
u(x + |
x)v(x + |
|
|
x) − u(x)v(x) |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
= |
lim |
|
u(x+Δx)v(x+Δx)−u(x)v(x+Δx)+u(x)v(x+Δx)−u(x)v(x) |
= |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
= |
lim |
|
|
u(x+Δx)−u(x) |
v(x + |
|
x) |
+ |
lim |
u(x) |
v(x+Δx)−v(x) |
= |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
x→0 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
x |
|
|
||||||||||||||
|
|
= u v + v |
u. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Теперь займемся производной частного. Сначала найдем произ- |
||||||||||||||||||||||||||||||||||||||||||
водную функции 1/v: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
− |
1 |
|
|
|
|
|
|
|
|
v(x) − v(x + |
x) |
|
|
|
|
|||||||||||
|
|
|
= |
|
lim |
|
v(x+Δx) |
v(x) |
|
= |
|
lim |
|
= |
|
|
|
||||||||||||||||||||||||||
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
x→0 |
|
|
x |
x) − v(x) |
x→0 x v(x + x) v(x) |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
= |
|
− |
|
lim |
v(x + |
lim |
|
|
1 |
|
|
|
= |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
x |
|
|
|
|
|
x→0 v(x + x) v(x) |
|
|
|
||||||||||||||||||||
|
|
|
|
|
= −v (x) |
|
1 |
= |
− |
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
v2(x) |
v2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Осталось воспользоваться формулой для производной произведения:
|
u |
|
|
= u |
|
1 |
|
= u |
1 |
+ u |
|
v |
|
= |
u |
|
uv |
= |
u v − v u |
. |
v |
|
|
· v |
|
v |
−v2 |
|
v − |
v2 |
|
||||||||||
|
|
|
|
|
|
v2 |
||||||||||||||

4.1. Производная функции |
195 |
|
|
4.1.5.Таблица производных основных элементарных функций. Производная сложной и обратной функций
1.(C) = 0, C = const.
До к а з а т е л ь с т в о. Пусть f(x) = C. Тогда
f (x) = lim |
f(x + |
x) − f(x) |
= |
lim |
C − C |
= 0. |
|
||||||
|
x |
x |
||||
x→0 |
|
x→0 |
|
|||
2.(sin x) = cos x.
Д о к а з а т е л ь с т в о. Имеем:
|
|
sin (x + |
x) |
|
sin x |
|
2 sin |
|
x cos x + |
x |
|
|
|||
= |
lim |
|
|
|
|
|
= |
lim |
|
|
2 |
2 |
|
= |
|
|
x |
− |
|
|
|
|
|
x |
|
|
|||||
(sin x) |
x→0 |
|
|
|
x→0 |
|
|
|
|
|
|||||
|
|
|
sin |
x |
|
|
x |
|
|
|
|||||
|
|
= lim |
|
2 |
|
lim cos x + |
|
|
= 1 · cos x = cos x. |
||||||
|
|
2x |
|
|
|
||||||||||
|
|
x→0 |
|
x→0 |
|
2 |
|
||||||||
Первый предел вычислили исходя из первого замечательного предела, второй — исходя из непрерывности функции cos x. 
3.(cos x) = − sin x.
До к а з а т е л ь с т в о. Поступим так же, как и при выводе формулы 2:
(cos x) = lim |
cos (x + |
x) − cos x |
= lim |
||||||||
|
|
|
|||||||||
|
x→0 |
|
|
|
|
x |
|
|
|
||
|
|
|
|
|
sin |
x |
|
|
|
x |
|
= |
− |
lim |
|
|
|
2 |
lim |
sin |
x + |
|
|
|
|
2x |
|
||||||||
|
x→0 |
|
|
x→0 |
|
2 |
|||||
4. (tg x) = |
1 |
|
|
. |
|
|
|
|
|
||
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
||||||
|
|
cos |
x |
|
|
|
|
|
|||
− |
2 sin |
x sin |
x + |
x |
|
|
|
|
2 |
x |
2 |
= |
|||
|
|
|
|||||
= −1 · sin x = − sin x.

196 |
|
|
|
|
|
|
|
Глава 4. Дифференциальное исчисление |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Д о к а з а т е л ь с т в о. На основании |
формул |
2, |
|
3 |
и правила |
||||||||||||||||||
дифференцирования частного (4.6) имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(tg x) = |
|
sin x |
|
= |
(sin x) cos x − (cos x) sin x |
= |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
cos x |
|
|
cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
= |
cos2 x + sin2 x |
|
= |
1 |
. |
||||||||||||
|
|
|
|
|
|
|
|
2 |
x |
|
|
|
|
|
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
cos x |
||||
5. (ctg x) = − |
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
sin2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Д о к а з а т е л ь с т в о. Поступим так же, как и при выводе фор- |
|||||||||||||||||||||||
мулы для производной tg x: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(ctg x) = |
|
|
cos x |
|
= |
(cos x) sin x − (sin x) cos x |
= |
|
|
|
|
|
|
|
|
|
|||||||
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
sin2 x |
2 |
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
= |
− sin |
|
x − cos |
x |
= |
|
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
cos2 x |
|
|
|
|
|
− cos2 x |
||||||
6. (ax) = ax ln a.
Д о к а з а т е л ь с т в о. Воспользуемся |
|
определением производ- |
|||||||||||||
ной (4.1) и следствием из второго замечательного предела. Тогда |
|||||||||||||||
(ax |
lim |
ax+Δx |
ax |
= lim |
|
ax |
|
a |
x − 1 |
|
= |
|
|
|
|
x− |
|
|
|
|
|
|
|
|
|
||||||
) = |
x→0 |
|
x→0 |
x |
|
|
|
|
|
||||||
|
|
|
|
= lim |
|
x |
lim |
ax a |
x − 1 |
|
= ax ln a. |
||||
|
|
|
|
|
|
|
|
x |
|
||||||
|
|
|
|
|
x→0 a |
|
x→0 |
|
|
||||||
7.(ex) = ex.
Д о к а з а т е л ь с т в о. Положив a = e в формуле 6, получим:
(ex) = ex ln e = ex.
Теорема 4.3. Если функция y = f(x) строго монотонна и непрерывна в некоторой окрестности точки x0, имеет производную в точке x0 и f (x0) = 0, то обратная функция x = f−1(y) имеет производную в соответствующей точке y0, y0 = f(x0), причем
(f−1(y0)) = − 1 . f (x0)

4.1. Производная функции |
197 |
|
|
Д о к а з а т е л ь с т в о. По теореме 3.16 обратная функция x = |
|
= f−1(y) существует, является монотонной и непрерывной в некоторой |
|
окрестности точки y0. Придадим аргументу y некоторое приращение |
|
y = 0 в |
этой точке. Соответствующее приращение x обратной |
функции в |
силу строгой монотонности тоже будет отличным от нуля. |
Следовательно, |
x |
|
|
1 |
|
|
|
|||
|
|
|
= |
|
|
, |
|
|||
|
|
|
y |
y/ |
|
|||||
|
|
|
|
|
x |
|||||
причем если y → 0, то и |
|
|
x |
→ 0. Перейдем к пределу в этом |
||||||
равенстве. Будем иметь: |
|
|
|
|
|
|
|
|
||
lim |
|
x |
|
= |
|
|
1 |
|
|
|
|
y |
|
lim |
(Δy/ x) |
||||||
y→0 |
|
|
||||||||
x→0
или f−1(y0) = 1/f (x0).
8.(loga x) = x ln1 a , a > 0, a = 1.
До к а з а т е л ь с т в о. Логарифмическую функцию y = loga x можно рассматривать как обратную функцию к показательной функции x = ay. Значит, применив теорему 4.3, получим:
(loga x) = |
1 |
= |
1 |
= |
1 |
. |
(ay) |
|
|
||||
|
|
ay ln a x ln a |
||||
9.(ln x) = x1 .
Д о к а з а т е л ь с т в о. Полагая a = e в формуле 8, получим:
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
(ln x) = |
|
|
|
= |
|
. |
|
|
|
|
||||
|
x ln e |
x |
|
|
|
|
||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
10. |
(arcsin x) = |
√ |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Д о к а з а т е л ь с т в о. Функция y = arcsin x является обратной |
|||||||||||||||||
к функции x = sin y, поэтому в силу теоремы 4.3 |
|
|
|
|
||||||||||||||
|
1 |
|
1 |
|
|
|
|
|
1 |
1 |
|
|||||||
|
(arcsin x) = |
|
= |
|
= |
|
|
= |
√ |
|
. |
|||||||
|
(sin y) |
cos y |
! |
|
|
|||||||||||||
|
1 − sin2 y |
1 − x2 |
||||||||||||||||

198 |
Глава 4. Дифференциальное исчисление |
|
|
Корень взят со знаком «+», так как y = arcsin x (−π/2, π/2), поэтому cos y > 0.
11. (arccos x) = − |
1 |
|
. |
|
|
|
|
|
|
|
|
||||
√ |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
1 − x |
|
|
|
|
|
|
|
||||
Д о к а з а т е л ь с т в о. Функция y = arccos x является обратной |
|||||||||||||||
к функции x = cos y, поэтому в силу теоремы 4.3 |
|
|
|
|
|||||||||||
(arccos x) = |
1 |
|
1 |
1 |
1 |
|
|||||||||
|
|
= − |
|
= − |
|
|
= − |
√ |
|
. |
|||||
(cos y) |
sin y |
! |
|
|
|||||||||||
1 − cos2 y |
1 − x2 |
||||||||||||||
Корень взят со знаком «+», так как y = arccos x (0, π), поэтому |
|||||||||||||||
sin y > 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12. (arctg x) = |
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
1 + x |
|
|
|
|
|
|
|
|
|
|
||||
Д о к а з а т е л ь с т в о. Функция y = arctg x является обратной к функции x = tg y, поэтому в силу теоремы 4.3
(arctg x) = |
|
1 |
|
= |
|
1 |
|
= cos2 y = |
1 |
|
|
= |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
1 + tg |
2 |
|
2 |
|||||||
|
(tg y) |
|
|
1/ cos |
y |
|
y |
1 + x |
|||||||
13. (arcctg x) = − |
1 |
|
. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
1 + x2 |
|
|
|
|
|
|
|
|
||||||
До к а з а т е л ь с т в о. Функция y = arcctg x является обратной
кфункции x = ctg y, поэтому в силу теоремы 4.3
(arcctg x) = |
1 |
= |
1 |
= − sin2 y = − |
1 |
= − |
1 |
. |
|
|
|
|
|||||
(ctg y) |
−1/ sin2 y |
1+ ctg2 y |
1+x2 |
Теорема 4.4. Если функция u = ϕ(x) имеет производную в точке x0, а функция y = f(u) — в соответствующей точке u0, u0 = ϕ(x0), то сложная функция y = f(ϕ(x)) имеет производную в точке x0 и справедлива следующая формула:
y (x0) = f (u0) ϕ (x0). |
(4.7) |

4.1. Производная функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
199 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Д о к а з а т е л ь с т в о. По определению производной (4.1) |
||||||||||||||||||||||||||||||||||
f (u0) = |
lim |
|
f(u0 + |
u) − f(u0) |
= |
|
lim |
|
f(u0) |
. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
u→0 |
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
u→0 |
|
|
u |
|
|
||||
На основании свойства 1 предела функции можно записать: |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
f(u0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u = 0, |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
= f |
|
(u0) + α(Δu), |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|||||||||||||||||||||
где α(Δu) есть БМФ при |
|
u → 0. Следовательно, |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
f(u0) = f (u0)Δu + α(Δu)Δu. |
|
|
|
|
|
|||||||||||||||||||||||
Последняя формула верна и при |
u = 0. Разделив обе части |
|||||||||||||||||||||||||||||||||
этого равенства на |
x, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
f(u0) |
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
u |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= f |
(u0) |
|
|
|
|
+ α(Δu) |
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|||||||
Теперь перейдем |
к |
пределу, когда |
|
|
x |
|
→ 0. Заметив, что и |
|||||||||||||||||||||||||||
u → 0, будем иметь: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
lim |
|
f(u0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
u |
|
|
||||||
|
|
|
|
|
|
= f |
|
(u0) |
|
lim |
|
|
|
|
+ |
|
lim |
α(Δu) |
|
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
x |
||||||||||||||||||||||
x→0 |
|
x |
|
|
|
|
|
x→0 |
|
|
|
|
|
x→0 |
|
|
|
|||||||||||||||||
Остается учесть, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|||||||||
|
|
|
|
f(u0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|||||||
|
lim |
|
|
|
x |
= |
|
|
f ϕ(x ) |
, |
|
lim |
|
|
= ϕ (x ), |
|||||||||||||||||||
|
x→0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
x→0 |
x |
· |
0 |
|
|
||||||||||||
lim |
α(Δu) |
|
|
|
|
= lim |
|
α(Δu) |
lim |
|
|
= 0 |
ϕ (x ) = 0, |
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
x→0 |
|
|
|
|
|
x |
|
x→0 |
|
|
|
|
|
|
x→0 |
x |
0 |
|
|
|||||||||||||||
и получим формулу (4.7).
Отметим, что формулу (4.7) для нахождения производной сложной функции y = f(ϕ(x)), ϕ(x) = u, можно кратно записать так:
yx = fu · ux. |
(4.8) |
14. (xα) = αxα−1, α R, α = 0.
