
Е. А. Ровба - Высшая математика
.pdf110 |
Глава 2. Аналитическая геометрия |
|
|
Теорема 2.4. Точка M плоскости принадлежит гиперболе (2.20) тогда и только тогда, когда абсолютная величина разности фокальных радиусов этой точки равна 2a:
|r1 − r2| = 2a. |
(2.21) |
Д о к а з а т е л ь с т в о. Необходимость. Убедимся, что для всякой точки M гиперболы абсолютная величина разности фокальных радиусов равна 2a.
Из рис. 2.11 видно, что фокальные радиусы гиперболы могут быть вычислены по формулам:
|
|
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
r1 = |
(x + c)2 + y2, |
r2 = (x − c)2 + y2. |
|
|
|
(2.22) |
||||||||||||||||||||||||||
Если точка M(x, y) принадлежит гиперболе, то ее координаты |
|||||||||||||||||||||||||||||||||||
удовлетворяют уравнению (2.20), откуда получаем: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
y2 |
|
x2 |
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
||||
|
|
= |
|
− 1, |
y2 = b2 |
|
− 1 = (c2 − a2) |
|
|
− 1 . |
|
|
|
||||||||||||||||||||||
|
b2 |
a2 |
a2 |
a2 |
|
|
|
||||||||||||||||||||||||||||
Вычисление r1 проводим тем же способом, что и при доказатель- |
|||||||||||||||||||||||||||||||||||
стве теоремы 2.3: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r1 = &(x + c)2 + (c2 − a2) |
x2 |
− 1 = |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
= & x2 + 2cx + c2 |
+ |
|
|
|
|
|
x2 − c2 − x2 + a2 |
= |
|
|
|
|
|||||||||||||||||||||
|
|
|
a2 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
= 'a2 + 2cx + |
c2 |
|
|
|
|
|
c |
|
2 |
|
|
|
c |
|
|
|
|
||||||||||||||||
|
|
|
x2 = |
' a + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
a2 |
a |
x |
|
|
= |
|
a + |
a |
x . |
|
|
|
|
||||||||||||||||||||
Аналогично находим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
r2 = |
a − |
|
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
x |
>c a. |
|||
Поскольку для |
гиперболы |
|
|x| a и |
c |
> |
|
a, то |
a |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
Значит, при раскрытии модулей надо смотреть знак выражения |
|
x, |
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
определяемый знаком аргумента x. Имеем два случая:

2.2. Кривые второго порядка |
|
|
|
|
|
|
|
111 |
|||
|
|
|
|
|
|
|
|
|
|||
1) |
для правой ветви гиперболы x a, поэтому |
|
|||||||||
|
|
c |
|
|
c |
|
(2.23) |
||||
|
r1 = |
|
x + a, |
r2 |
= |
|
x − a, |
r1 − r2 = 2a; |
|||
|
a |
a |
|||||||||
2) |
для левой ветви x −a, поэтому |
|
|
||||||||
|
|
c |
|
|
|
|
c |
|
(2.24) |
||
|
r1 = − |
|
x − a, |
r2 |
= − |
|
x + a, |
r2 − r1 = 2a. |
|||
|
a |
a |
|||||||||
В каждом из указанных случаев верно доказываемое равенство (2.21).
Достаточность. Покажем, что всякая точка M, абсолютная величина разности фокальных радиусов которой равна 2a, принадлежит гиперболе. В этих условиях, согласно формулам (2.22),
|
! |
|
|
|
! |
|
|
|
2 |
|
|
2 |
2 |
|
(x − c)2 + y2 |
2 |
|
||||||
|
|
(x + c)2 |
+ y2 − |
|
= 2a, |
||||||
|
|
|
|
|
|
± |
|
− |
|
|
|
! |
|
|
|
|
|
! |
|
|
|
|
|
|
|
(x + c) + y |
= 2a + |
(x c) |
+ y . |
||||||
Как и при доказательстве теоремы 2.3, возведем левую и правую части в квадрат:
!
(x + c)2 + y2 = 4a2 ± 4a (x − c)2 + y2 + (x − c)2 + y2,
!
±a (x − c)2 + y2 = cx − a2.
Последнее равенство снова возведем в квадрат:
a2 (x − c)2 + y2 = (cx − a2)2,
a2x2 − 2a2cx + a2c2 + a2y2 = c2x2 − 2a2cx + a4, (a2 − c2)x2 + a2y2 = a2(a2 − c2).
В данном случае c2 = a2 + b2. После замены a2 − c2 = −b2 будем иметь:
−b2x2 + a2y2 = −a2b2.
Деля левую и правую части полученного уравнения на −a2b2, приходим к каноническому уравнению гиперболы (2.20). Этим доказано, что точка M принадлежит гиперболе. 

112 |
Глава 2. Аналитическая геометрия |
|
|
Замечание 2.4. Утверждение теоремы 2.4 может быть использовано в качестве определения гиперболы.
Определение 2.25. Эксцентриситетом гиперболы называется
число
ε = ac ,
характеризующее ее форму. Так как c > a, то ε > 1.
Понятие эксцентриситета позволяет переписать формулы (2.23) и (2.24) для фокальных радиусов точки M, лежащей соответственно на правой и левой ветвях гиперболы, следующим образом:
1)r1 = εx + a, r2 = εx − a для правой ветви;
2)r1 = −εx − a, r2 = −εx + a для левой ветви.
Определение 2.26. Если a = b, т.е. действительная и мнимая полуоси равны, то уравнение гиперболы принимает вид x2 − y2 = a2. Такая гипербола называется равнобочной. Ее асимптоты образуют прямой угол и являются биссектрисами координатных углов.
Определение 2.27. Уравнение
y2 |
− |
x2 |
= 1 |
(2.25) |
b2 |
a2 |
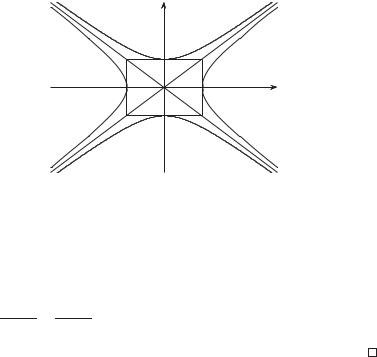
задает гиперболу, действительной и мнимой осями которой служат соответственно мнимая и действительная оси гиперболы (2.20). Гиперболы (2.20) и (2.25) имеют общие полуоси, асимптоты и основной прямоугольник и называются сопряженными.
На рис. 2.12 сопряженная гипербола изображена штриховой
линией, ее фокусы обозначены F |
|
и F |
. |
|||||
|
|
|
|
1 |
2 |
|||
Пример 2.12. Составить каноническое уравнение гиперболы, |
||||||||
проходящей через |
|
√ |
|
√ |
|
и имеющей эксцентриситет |
||
|
|
3, 2 |
||||||
√ |
|
|
точку |
M |
|
|
|
|
ε= 2.
Ре ш е н и е. Согласно определению эксцентриситета
|
c |
√ |
|
√ |
|
|
2 |
2 |
|
|
|
|
|
||||||
ε = |
|
= 2, c = 2a, c |
|
= 2a |
. |
||||
a |
|
||||||||
2.2. Кривые второго порядка |
113 |
|
|
|
y |
|
|
|
|
c |
F2 |
|
|
F1 |
b |
|
F2 |
|
|
|
|
||
−c |
O |
a |
c |
x |
|
|
|
||
|
−c F1 |
|
|
|
|
Рис. 2.12 |
|
|
|
Поскольку для всякой гиперболы верно равенство c2 = a2 + b2, то в нашем случае b2 = c2 −a2 = 2a2 −a2 = a2, т.е. гипербола равнобочная.
Подставим координаты данной по условию точки M в канониче-
ское уравнение (2.20): |
|
|
|
|
|
|
|
|
|||||||||
|
√ |
|
|
2 |
|
|
√ |
|
|
2 |
|
3 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
3 |
|
|
|
|
2 |
|
|
|
|
|
||||||
|
a2 |
|
− |
|
|
|
|
|
= 1, |
|
− |
|
= 1, |
|
= 1, a2 = 1. |
||
|
b2 |
a2 |
a2 |
a2 |
|||||||||||||
Значит, уравнение искомой гиперболы имеет вид x2 − y2 = 1.
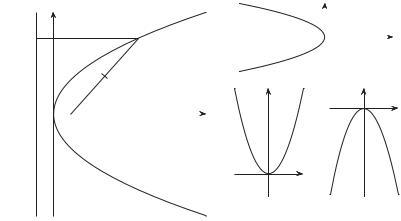
2.2.4. Парабола
Определение 2.28. Парабола (рис. 2.13) — это геометрическое место точек плоскости, координаты которых удовлетворяют уравнению
y2 = 2px, p > 0, |
(2.26) |
называмому каноническим уравнением параболы.
Из определения следует, что парабола:
1)симметрична относительно оси Ox;
2)лежит в правой полуплоскости, т.е. x 0;
3)проходит через начало координат.
114 |
Глава 2. Аналитическая геометрия |
|
|
|
y |
|
d |
||
|
|
|
|||
|
|
|
|
M(x, y) |
|
|
|
|
|
||
|
|
|
|
r |
|
|
|
F |
|
|
|
|
|
|
|
|
|
− |
p O |
p |
|
x |
|
2 |
2 |
|
|||
Ly2 = 2px
Рис. 2.13
|
y |
|
O |
|
|
|
|||
|
|
|
||
|
|
|
x |
|
|
|
|
y2 = −2px |
|
y |
|
|
y O |
|
x
Ox
x2 = 2py |
x2 = −2py |
Рис. 2.14
Уравнение y2 = −2px задает параболу, симметричную параболе (2.26) относительно оси ординат. Уравнения x2 = 2py и x2 = −2py определяют «повернутые» параболы, чьи оси симметрии совпадают с осью ординат (рис. 2.14).
Определение 2.29. Ось абсцисс, которая является осью симметрии параболы, называется осью параболы.
Определение 2.30. Начало координат O(0, 0) называется вершиной параболы.
Определение 2.31. Точка F (p/2, 0) (см. рис. 2.13) называется
фокусом параболы.
Определение 2.32. Прямая L, задаваемая уравнением x = −p/2 (см. рис. 2.13), называется директрисой параболы.
Определение 2.33. Расстояние от фокуса до директрисы, равное p, называется параметром параболы.
Определение 2.34. Для любой точки M(x, y) параболы отрезок r = MF (см. рис. 2.13) называется фокальным радиусом параболы.
Теорема 2.5. Точка M плоскости принадлежит параболе тогда и только тогда, когда эта точка равноудалена от фокуса F и директрисы L.
2.2. Кривые второго порядка |
|
|
|
|
|
115 |
||
|
|
|
||||||
Д о к а з а т е л ь с т в о. Отметим, что для всякой точки M(x, y) |
||||||||
плоскости фокальный радиус r и расстояние |
до директрисы d |
|||||||
(см. рис. 2.13) вычисляются по формулам: |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
r = ' x − |
p |
|
2 |
|
p |
|
|
|
|
|
+ y2 |
, d = x + |
|
. |
(2.27) |
||
2 |
2 |
|||||||
Необходимость. Докажем, что для всякой |
точки |
M параболы |
||||||
фокальный радиус r равен расстоянию до директрисы d.
Если точка M(x, y) принадлежит параболе, то координаты x и y удовлетворяют каноническому уравнению (2.26). Тогда, согласно
формулам (2.27), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r = ' x − |
p |
2 |
+ 2px = & x2 |
|
|
|
p2 |
+ 2px = |
|||||||||||
|
|
|
− px + |
|
|||||||||||||||
2 |
|
4 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 'x2 + px + |
|
p2 |
p |
2 |
= |
x + |
|
p |
= d. |
||||||||||
|
4 = ' x + |
2 |
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Достаточность. Предположим, |
|
что |
точка |
|
M равноудалена |
||||||||||||||
от фокуса и директрисы, и докажем, что эта точка принадлежит параболе.
В соответствии с предположением для точки M(x, y) имеет место
равенство r = d. Согласно формулам (2.27) это означает, что |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
p |
|
|
|
|
|
||||
|
|
|
|
|
' x − |
|
+ y2 = |
|
x + |
|
|
. |
|
|
|
|
||||
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|||||||
Преобразуем это уравнение, возведя обе |
его части |
в квадрат: |
||||||||||||||||||
x − |
p |
|
2 |
|
|
|
p |
2 |
|
|
|
|
|
p |
2 |
|
p |
2 |
||
|
|
|
+ y2 |
= x + |
|
, y2 = |
x + |
|
|
|
− x − |
|
|
. |
||||||
2 |
|
2 |
2 |
2 |
||||||||||||||||
Применив к правой части последнего равенства формулу разности квадратов, получим уравнение y2 = 2px, которое представляет собой каноническое уравнение параболы (2.26). 
Замечание 2.5. Утверждение теоремы 2.5 может использоваться в качестве определения параболы.
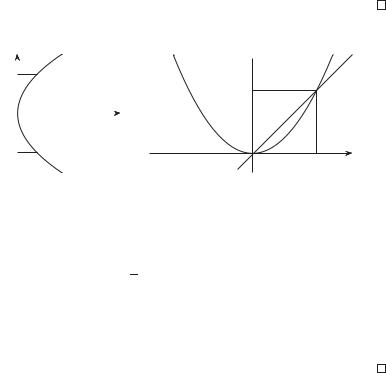
116 |
|
Глава 2. Аналитическая геометрия |
|||
|
|
|
|
||
Поскольку для |
точек M(x, y) |
параболы (2.26) x 0, то из |
|||
теоремы 2.5 следует, что фокальный радиус таких точек |
|||||
|
|
p |
|
p |
|
|
|
|
|
|
|
|
|
|
|
||
|
r = d = x + 2 |
= x + 2 . |
|||
Пример 2.13. Составить уравнение симметричной относительно оси Ox параболы с вершиной в начале координат, если длина некоторой хорды этой параболы, перпендикулярной оси Ox, равна 16, а расстояние от вершины до этой хорды равно 4.
Р е ш е н и е. Из условия следует, что точка M(4, 8) лежит на параболе (рис. 2.15). Подставим координаты M в каноническое уравнение параболы (2.26): 82 = 2p · 4, 2p = 64/4 = 16.
Зная параметр, записываем искомое уравнение: y2 = 16x.
y |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
M |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
4 |
x |
x2 = 2py |
|
|
|
|
|
||
−8 |
|
|
y2 = 2px |
|
|
|
|
|
|||
y 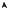
M
8
√  2 8
2 8
O |
8 x |
Рис. 2.15 |
Рис. 2.16 |
Пример 2.14. Составить уравнение симметричной относительно оси Oy параболы с вершиной в начале координат, если известно, что
эта парабола отсекает на биссектрисе первого и третьего координат-
√
ных углов хорду длиной 8 2.
Р е ш е н и е. Из условия следует, что на параболе лежит точка M(8, 8) (рис. 2.16). Подставляем координаты точки M в каноническое уравнение x2 = 2py данной параболы: 82 = 2p · 8, 2p = 8.
Итак, искомое уравнение имеет вид x2 = 8y.
2.2. Кривые второго порядка |
117 |
|
|
2.2.5.Кривые второго порядка со смещенным центром
Центр эллипса и гиперболы, а также вершина параболы могут быть помещены в любую точку C(x0, y0) плоскости. При этом канонические уравнения соответствующих кривых преобразуются к следующему виду:
(x − x0)2 |
+ |
(y − y0)2 |
= 1, |
(x − x0)2 |
− |
(y − y0)2 |
= 1, |
|
a2 |
b2 |
a2 |
b2 |
|||||
|
|
|
(y − y0)2 = 2p (x − x0) .
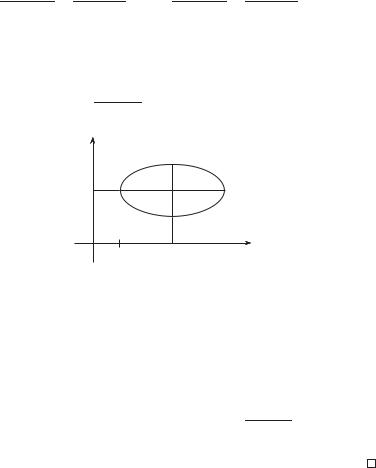
Например, эллипс с центром в точке C(3, 2) и полуосями a = 2 и b = 1 (рис. 2.17) имеет уравнение
|
(x − 3)2 |
+ (y |
− |
2)2 |
= 1. |
|
4 |
|
|
|
|
y |
|
|
|
|
|
|
|
|
1 |
2 |
|
2 |
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
O |
1 |
3 |
|
x |
|
|
|
|
|
|
|
|
Рис. 2.17 |
|
|||
Пример 2.15. Установить вид линии второго порядка, заданной уравнением 9x2 − 4y2 + 18x + 8y − 31 = 0.
Р е ш е н и е. Выделим в данном уравнении полные квадраты по каждой из переменных:
9(x2 + 2x + 1) − 9 − 4(y2 − 2y + 1) + 4 − 31 = 0,
9(x + 1)2 |
|
4(y |
|
1)2 = 36, |
(x + 1)2 |
(y − 1)2 |
= 1. |
||
− |
− |
4 |
− |
9 |
|||||
|
|
|
|
||||||
Получили каноническое уравнение |
гиперболы |
с центром в точке |
|||||||
C(−1, 1) и полуосями a = 2 и b = 3. |
|
|
|
|
|||||

118 |
Глава 2. Аналитическая геометрия |
|
|
Пример 2.16. Установить вид линии второго порядка, заданной уравнением x2 − 4x − 4y = 0.
Р е ш е н и е. Выделим в заданном уравнении полный квадрат по переменной x:
(x2 − 4x + 4) − 4 − 4y = 0, (x − 2)2 = 4y + 4, (x − 2)2 = 4(y + 1).
Получили каноническое уравнение параболы с вершиной в точке C(2, −1) и параметром p = 2.
Глава 3
Предел
последовательности и функции
3.1. Числовая последовательность
3.1.1. Понятие числовой последовательности
Определение 3.1. Пусть N — множество натуральных чисел. Если каждому натуральному числу n поставлено в соответствие некоторое число xn, то говорят, что определена числовая последовательность. Числа xn, n N, называют элементами или членами последовательности. Для числовой последовательности мы будем использовать следующие обозначения:
x1, x2, . . . , xn, . . . ; {xn}; xn, n N.
Последовательности встречались при изучении математики в средней школе. Например, бесконечная геометрическая прогрессия 1, q, q2, . . . , qn, . . . , |q| < 1, является числовой последовательностью.
Определение 3.2. Последовательности {xn + yn}, {xn − yn}, {xnyn}, {xn/yn} называются соответственно суммой, разностью, произведением и частным двух последовательностей {xn} и {yn} (для частного yn = 0, n N).
Определение 3.3. Последовательность {xn} называется ограниченной, если существует такое число M > 0, что для любого n N
