
Е. А. Ровба - Высшая математика
.pdf
130 |
Глава 3. Предел последовательности и функции |
|
|
3.1.6. Предельный переход в неравенствах
Теорема 3.2. Если
lim xn = a
n→∞
иначиная с некоторого номера xn b, то a b.
До к а з а т е л ь с т в о. Предположим противное. Пусть a < b. По определению предела последовательности для всякого положительного числа, в том числе и для ε = b − a,
Nε N n > Nε |xn − a| < ε = b − a,
или
−(b − a) < xn − a < b − a.
Из правого неравенства получаем: для всякого n > Nε имеет место неравенство xn < b, что противоречит условию теоремы. 
Замечание 3.4. Из того, что все элементы сходящейся к a последовательности {xn} строго больше b, вообще говоря, не следует строгое неравенство a > b. Например, для всякого n N верно, что 1/n > 0, однако
lim 1 = 0.
n→∞ n
Следствие 3.1. Если элементы сходящихся последовательностей {xn} и {yn} начиная с некоторого номера удовлетворяют неравенству xn yn, то и их пределы удовлетворяют неравенству
lim xn lim yn.
n→∞ n→∞
Д о к а з а т е л ь с т в о. Действительно, начиная с некоторого номера будем иметь, что yn − xn 0. Следовательно, по теореме 3.2
lim (yn − xn) 0,
n→∞
а по свойству 4 сходящихся последовательностей
lim yn − lim xn 0.
n→∞ n→∞

3.1. Числовая последовательность |
131 |
|
|
С помощью данного следствия можно доказать приведенную ниже теорему.
Теорема 3.3 (о сжатой последовательности). Пусть даны три последовательности {xn}, {yn}, {zn} и начиная с некоторого номера выполняется двойное неравенство xn yn zn. Если последовательности {xn} и {zn} имеют один и тот же предел a, то последовательность {yn} также имеет предел a.
Следующую теорему попробуйте доказать самостоятельно.
Теорема 3.4 (о сохранении знака). Если последовательность {xn} сходится к положительному числу a, то найдется такой номер N0 N, что для всех n > N0 окажется xn > 0.
3.1.7. Монотонные последовательности
Определение 3.10. Последовательность {xn} называется возрастающей, если для всех n N выполняется неравенство xn xn+1, и убывающей, если для n N верно, что xn+1 xn.
Определение 3.11. Возрастающая и убывающая последовательности называются монотонными.
Определение 3.12. Если для всех n N верно неравенство xn < xn+1, то последовательность {xn} называется строго возрастающей; если же для n N верно, что xn+1 < xn, — строго убывающей.
Определение 3.13. Строго возрастающие и строго убывающие последовательности называются строго монотонными.
Пример 3.8. Последовательность
0, 12 , 23 , . . . , n −n 1 , . . .
строго возрастающая и ограниченная. Очевидно, что она сходится, причем
lim n − 1 = 1.
n→∞ n
Пример 3.9. Последовательность 2, 4, 8, . . . , 2n, . . . строго возрастающая неограниченная. Она является ББП.

132 |
|
|
Глава 3. |
Предел последовательности и функции |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
Пример 3.10. Последовательность |
|
|
|
|
|
|||||||||
|
|
|
|
√ |
|
|
|
|
n |
|
|
|
|
|
|
|
1, |
|
3 |
, . . . , |
sin |
|
π, . . . |
|
|
|
|||
|
|
2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
n + 1 |
|
|
|
|||||
строго убывающая ограниченная, причем |
|
|
|
|
||||||||||
|
n |
|
|
|
|
π |
π |
|
||||||
lim sin |
|
π = |
lim sin |
π |
|
|
|
= lim sin |
|
|
= 0. |
|||
n→∞ |
n + 1 |
n→∞ |
|
− n + 1 |
|
n→∞ |
n + 1 |
|
||||||
Пример 3.11. Последовательность 0, 1, 1, 2, 2, 3, 3, . . . , [n/2], . . .
(напомним, что квадратные скобки обозначают целую часть числа) возрастающая, но не строго возрастающая ББП.
Оказывается, что все монотонные ограниченные последовательности обладают общим свойством — они сходятся.
Теорема 3.5. Монотонная ограниченная последовательность сходится.
Таким образом, ограниченность монотонной последовательности является необходимым и достаточным условием сходимости.
Замечание 3.5. Всякая монотонная последовательность является либо сходящейся, либо бесконечно большой (обоснуйте это самостоятельно). Однако не всякая сходящаяся последовательность является монотонной. В этом можно убедиться на примере 3.1 бесконечно малой, а значит, и сходящейся, но не монотонной последовательности.
Рассмотрим важный пример монотонной ограниченной последовательности.
Теорема 3.6. Последовательность
1 |
n |
|
|
xn = 1 + |
|
|
(3.1) |
n |
|||
сходится. |
|
|
|
Д о к а з а т е л ь с т в о. Покажем, что |
последовательность (3.1) |
||
возрастает. Действительно, с помощью формулы бинома Ньютона (B.5) можно записать:
xn = 1 + n1 n = n Cnk n1k . k=0

3.1. Числовая последовательность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
133 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Поскольку по определению (B.6) биномиальные коэффициенты |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Cnk = |
|
|
|
|
|
|
n! |
|
= |
n(n − 1)(n − 2) · · · (n − k + 1) |
, |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
k! (n − k)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
= 1 + n |
1 |
+ |
n(n − 1) |
|
1 |
|
+ |
n(n − 1)(n − 2) |
|
|
1 |
|
+ . . . + |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
n3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
2! |
|
|
|
|
|
|
+ |
3! |
|
|
|
|
|
|
|
|
|
n·!· · |
|
− |
|
|
− |
nn . |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n(n |
− |
|
1)(n |
− |
|
(n |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
n |
|
|
|
|
|
|
1) |
|
|
1 |
|
|||||||||||
|
Преобразуем полученное выражение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
xn = 2 + |
|
|
1 |
− |
|
|
+ |
|
|
1 − |
|
|
|
1 − |
|
+ . . . + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
2! |
n |
3! |
n |
n |
|
− |
|
|
|
n |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
− n |
|
|
− n |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
2 |
|
. . . 1 |
|
|
n − 1 |
|
|
. |
(3.2) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
Теперь запишем по этой же формуле (n + 1)-й член: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
xn+1 = 2 + |
1 |
1 − |
|
|
1 |
|
|
+ |
1 |
|
|
1 − |
|
|
1 |
|
|
1 − |
|
|
2 |
|
|
+ . . . + |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
2! |
n + 1 |
3! |
n + 1 |
n + 1 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
+ |
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
n − 1 |
|
+ |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
n! |
− n + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− n + 1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
− n + 1 |
· · · |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
1 |
|
|
|
|
1 − |
|
|
1 |
|
1 − |
|
|
2 |
|
· · · |
|
1 − |
|
n |
|
|
. |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(n + 1)! |
|
n + 1 |
n + 1 |
|
n + 1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Сравним члены xn и xn+1. Очевидно, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
1 − |
|
|
< 1 − |
|
, k = 1, 2, . . . , n − 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
n + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
Поэтому первые n слагаемых xn+1 не меньше соответствующих слагаемых xn. Учитывая, что xn+1 содержит еще одно дополнительное неотрицательное слагаемое, получим, что для любого n N верно неравенство xn < xn+1, т.е. последовательность xn возрастает.
Далее докажем, что рассматриваемая последовательность (3.1)
ограничена. По формуле (3.2) |
|
|
|
|
|
|
|||
1 1 |
1 |
|
n |
1 |
|
||||
xn < 2 + |
|
+ |
|
+ . . . + |
|
= 1 + |
|
|
. |
2! |
3! |
n! |
k=1 |
k! |
|||||
|
|
|
|
|
|
|
|
|
|

134 |
Глава 3. Предел последовательности и функции |
||||||
|
|
|
|
|
|
|
|
|
Воспользуемся неравенством (B.4). Тогда |
|
|||||
|
1 |
|
1 |
|
|
||
|
xn < 1 + 2 − |
|
|
= 3 − |
|
< 3, |
(3.3) |
|
n |
n |
|||||
что и доказывает ограниченность последовательности {xn}.
Будучи монотонной и ограниченной, последовательность (3.1) сходится по теореме 3.5.
Определение 3.14. Предел последовательности (3.1), существующий в силу теоремы 3.6, обозначается буквой e и называется посто-
янной Эйлера: |
|
n |
|
|
1 |
(3.4) |
|||
n→∞ 1 + n |
. |
|||
e = lim |
|
|
|
|
Число e известно как основание натуральных логарифмов. Из соотношений (3.2) и (3.3) следует, что 2 < e < 3. Можно доказать, что число e является иррациональным, e = 2,7182 . . . . Это число играет существенную роль в математике и ее приложениях.
3.1.8. Непрерывное начисление процентов
В банковской системе, как правило, практикуются дискретные проценты по вкладам. Если начальная сумма вклада составляла S0 денежных единиц, p — годовая процентная ставка, представленная в виде десятичной дроби, и проценты начисляются 1 раз в год, то каждый год вклад будет увеличиваться в (1 + p) раз. Таким образом, через t лет сумма вклада составит
S = S0(1 + p)t.
Если проценты начисляются не 1 раз в год, а n раз, то при сохранении годовой процентной ставки p сумма вклада каждый раз будет увеличиваться в (1 + p/n) раз. По прошествии t лет таких увеличений произойдет tn и сумма вклада составит
|
1 + |
p |
|
tn |
(3.5) |
S = S0 |
|
. |
|||
n |
Некоторые сложные экономические процессы по своей природе подразумевают столь частое начисление процентов, что его можно

3.1. Числовая последовательность |
135 |
|
|
считать непрерывным. Для таких процессов количество n начислений в год принимает очень большие значения, которые можно условно считать близкими к бесконечности. Поэтому сумму S вклада в момент времени t в таких случаях можно определить, если в формуле (3.5)
перейти к пределу при n |
→ ∞ |
. Предположим, что процентная ставка |
|||||||||||
|
|
|
|
|
1 |
, и t |
N. По свойству 4 |
||||||
p = 1, т.е. вклад удваивается каждый год |
|
||||||||||||
сходящихся последовательностей и определению числа e (3.4) |
|||||||||||||
S = lim S |
|
|
1 |
tn |
= S |
|
lim |
1 + |
1 |
n |
t = S |
et. |
|
|
1 + n |
|
|
n |
|
||||||||
n→∞ |
0 |
|
0 |
n→∞ |
|
|
0 |
|
|||||
Можно доказать, что для произвольной процентной ставки p и |
|||||||||||||
любого (не обязательно целого) времени t > 0 |
|
|
|
||||||||||
|
|
|
|
S = S0ept. |
|
|
|
|
|
(3.6) |
|||
Соотношение (3.6) определяет закон непрерывного начисления процентов. Процентная ставка p при непрерывном начислении процентов называется силой роста.
Отметим, что чем чаще начисляются проценты, тем быстрее растет вклад. Данный факт объясняется дополнительной прибавкой сложных процентов, т.е. процентов от процентов. При фиксированной годовой ставке p вклад растет быстрее всего, если проценты начисляются непрерывно.
Поясним сказанное на примере.
Пример 3.12. Предположим, что начальный вклад S0 = 1, процентная ставка p = 1 и проценты начисляются n раз в год. Вычислим по формуле (3.5) размер вклада через год для некоторых значений n:
|
|
S = 1 + |
1 |
|
10 |
||
n = 1: S = (1 + 1)1 = 2; n = 10: |
≈ 2,594; |
||||||
|
|||||||
10 |
|||||||
n = 100: S = 1 + |
1 |
|
100 |
|
|
|
|
≈ 2,705. |
|
|
|||||
|
|
|
|||||
100 |
|
|
|||||
В случае непрерывного начисления процентов через год вклад вырастет максимально и, согласно формуле (3.6), составит
S = e1 = e ≈ 2,718.
1Разумеется, не стоит рассчитывать на такие проценты в реальной жизни.
136 |
Глава 3. Предел последовательности и функции |
|
|
3.2. Функциональная зависимость
3.2.1. Понятие функции
При изучении явлений природы, физических, экономических и других процессов часто встречаются с совокупностью переменных величин, которые связаны между собой так, что значения одних величин полностью определяют значения других. Например, площадь S круга однозначно определяется значением его радиуса с помощью формулы S = πr2.
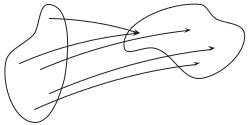
Определение 3.15. Пусть X и Y — два произвольных множества (рис. 3.4).
Y
X
Рис. 3.4
Если каждому элементу x из множества X по некоторому правилу f поставлен в соответствие единственный элемент y из множества Y , то говорят, что задана функция f. Функцию f, как правило, обозначают y = f(x) или f : X → Y . При этом x называется независимой переменной или аргументом функции, y — зависимой переменной или значением функции. Множество X называется областью определения или областью существования функции f и обозначается D(f). Множество всех значений, принимаемых функцией f, когда аргумент x пробегает всю область определения X, называется множеством значений функции f и обозначается E(f):
E(f) = y Y y = f(x), x X .
Очевидно, что множество значений функции E(f) содержится в множестве Y . При этом Y может также содержать элементы, не входящие в E(f) (рис. 3.4).

3.2. Функциональная зависимость |
137 |
|
|
Определение 3.16. Если X R и Y R, т.е. X и Y являются числовыми множествами, то функция f : X → Y называется числовой.
√ |
|
|
|
Пример 3.13. Функция y = 1 − x2 определена на |
отрезке |
||
[−1, 1], т.е. областью определения является множество X = |
[−1, 1]. |
||
Множеством значений функции в данном случае является отрезок [0, 1], или Y = [0, 1].
Определение 3.17. Функция, все значения которой равны между собой, называется постоянной. Постоянную функцию часто обозначают так же, как и то единственное значение, которое она принимает.
Определение 3.18. Графиком функции называется множество
всех точек плоскости вида |
|
x; f(x) , т.е. координаты x и y точек |
|
графика связаны |
соотношением y = f(x). |
||
|
|
|
|
Например, графиком функции y = x2 является парабола. Естественно, что графиком функции не обязательно является сплошная кривая. В частности, графиком функции y = n! будет бесконечное множество изолированных точек (нарисуйте!).
1 |
, f(−x), если f(x) = 1 + x + x2. |
Пример 3.14. Найти f(2), f x |
Р е ш е н и е. Очевидно, что f(2) = 1 + 2 + 22 = 7. Если вместо независимой переменной подставить выражение 1/x, то получим:
1 |
|
1 |
1 |
|
2 |
1 + x + x2 |
||||
f |
|
|
= 1 + |
|
+ |
|
|
= |
|
. |
x |
x |
x |
x2 |
|||||||
Аналогично f(−x) = 1 + (−x) + (−x)2 = 1 − x + x2.
Пример 3.15. Определить область существования функции
!
y = x2 − 3x + 2.
Р е ш е н и е. В этом случае подкоренное выражение должно быть неотрицательно: x2 − 3x + 2 0. Решив это неравенство, получим, что областью определения является множество D = (−∞, 1] [2, +∞). 
138 |
Глава 3. Предел последовательности и функции |
|
|
3.2.2. Способы задания функции
Чтобы задать функцию, требуется указать, как по каждому значению аргумента x находить соответствующее значение функции y = f(x).
Мы рассмотрим четыре наиболее распространенных способа задания функции: аналитический, неявный, табличный и графический.
Аналитический способ
Если зависимость между переменными выражена с помощью формул, то говорят, что функция задана аналитически. Формула, задающая функцию, указывает совокупность действий, которые нужно выполнить в определенном порядке, чтобы получить соответствующее значение функции.
|
3.16 |
|
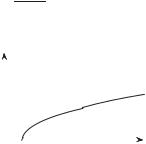
Рассмотрим функцию y = |
|
x − 1. Она определена |
|
Пример |
|
. |
|
√ |
||
на промежутке [1, +∞). Чтобы вычислить значение функции для всех x [1, +∞), необходимо из значения аргумента x вычесть единицу и извлечь из полученного числа квадратный корень. Множеством зна-
чений является промежуток [0, +∞). График функции — множество
√
всех точек плоскости (x, x − 1), где переменная x пробегает область определения [1, +∞) (рис. 3.5).
y |
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3 |
|
|
|
|
|
|
|
|
y = |
|
|
|
x − 1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
1 |
3 |
|
|
5 |
|
|
|
x |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
Рис. 3.5
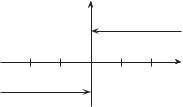
Пример 3.17. Пусть
1,
y = 0,
−1,
если x (0, +∞), |
(3.7) |
если x = 0, |
|
если x (−∞, 0). |
|
3.2. Функциональная зависимость |
139 |
|
|
Данная функция выражена с помощью нескольких формул. Областью ее определения является вся числовая прямая, множество значений состоит из трех элементов: −1, 0, 1. График изображен на рис. 3.6. Эту функцию обозначают y = sign x.
|
|
y |
|
|
|
|
|
|
y = sign x |
|
|
|
|
1 |
|
|
|
−2 |
−1 |
|
|
|
|
O |
1 |
2 |
x |
||
|
|
|
−1 |
|
|
|
Рис. 3.6 |
|
|
||
Неявный способ
Предположим, что значения двух переменных x и y связаны между собой некоторым уравнением, например:
2 |
= 0, |
2 |
2 |
= 1, |
3 |
3 |
= 3xy, |
2 |
2 |
) |
2 |
2 |
2 |
. |
y − x |
x + y |
|
x + y |
|
(x |
+ y |
|
= x |
− y |
Тогда каждому значению переменной x можно поставить в соответствие множество решений Yx такого уравнения относительно переменной y. Полученное соответствие, вообще говоря, не является функцией.
Всамом деле, для каких-то значений x множество Yx может оказаться пустым, а для других x оно может содержать два элемента или более. Однако, накладывая определенные ограничения на выбор переменных x и y, часто удается добиться, чтобы для всех значений x из выбранного диапазона множество Yx содержало ровно один элемент.
Втаких случаях можно говорить о том, что определена функция y переменной x. Описанный способ задания функции называется неявным.
Пример 3.18. Уравнение y −x2 = 0 легко решается относительно переменной y. Для всякого x R существует единственное решение y = x2, которое является функцией, заданной аналитически.
Вообще, всякая аналитически заданная функция y = f(x) может быть представлена в виде уравнения y − f(x) = 0.
