Операції перетину, об'єднання і різниці нечітких множин

Хай і – довільні (кінцеві або нескінченні) нечіткі множини, задані на одному і тому ж універсумі X.

Перетин. Перетином двох нечітких множин і називатимемо деяку третю нечітку множину , задану на цьому ж універсумі X, функція приналежності якого визначається за наступною формулою:

для будь-якого . (4.3)

Операція перетину нечітких множин по аналогії із звичайними множинами позначається знаком "∩". В цьому випадку результат операції перетину двох нечітких множин записується у вигляді: = ∩ .

В цьому випадку – нечітка множина з функцією приналежності , яка визначається по формулі (4.3). Як неважко відмітити, перетин ∩ є найбільша нечітка підмножина , яка міститься одночасно в нечітких множинах і .

Операцію перетину нечітких множин в сенсі (4.3) іноді називають min-перетином або - перетином. Останнє позначення пов'язане з визначенням логічної операції "І", яка в математичній логіці позначається знаком " ". Відповідно функція приналежності перетину в цьому випадку записується у вигляді: для будь-якого .

При цьому знак " " використовується як синонім операції знаходження мінімального значення. Оскільки в практиці нечіткого моделювання ця операція використовується найчастіше, надалі, кажучи про перетин нечітких множин, якщо явно не вказане інше, ми матимемо на увазі min-перетин ( - перетин).

В якості прикладу розглянемо скінченну нечітку множину , яка представляє в деякому контексті властивість "невелике натуральне число", і дорівнює: ={<1, 1.0>, <2, 1.0>, <3, 0.9>, <4, 0.8>, <5, 0.6>, <6, 0.5>, <7, 0.4>, <8, 0.2>, <9, 0.1>}, і скінченна нечітка множина , яка представляє властивість "натуральне число, яке приблизно дорівнює двом", і дорівнює: ={<1, 0.5>, <2, 1.0>, <3, 0.6>, <4, 0.4>, <5, 0.2>,<6, 0>,<7, 0>,<8, 0>, <9, 0>}.

Тоді нечітка множина як результат операції перетину  =  ∩  буде дорівнювати: ={<1, 0.5>, <2, 1.0>, <3, 0.6>, <4, 0.4>, <5, 0.2>, <6, 0>, <7, 0>, <8, 0>, <9, 0>}. Змістовно нечітка множина може представляти в цьому ж контексті "невелике натуральне число, яке приблизно дорівнює двом".

Результат операції перетину двох і більшої кількості нечітких множин, заданих на одному і тому ж універсумі X, також можна зобразити графічно в декартовій системі координат на площині. Цей спосіб особливо зручний для візуалізації операцій з нескінченними нечіткими множинами. В даному випадку кожна з нечітких множин зображається відповідною функцією приналежності, а функція приналежності результату операції перетину зображається потовщеною лінією. Для додаткової наочності область, що розташовується нижче за значення результуючої функції приналежності, зображається затемненою.

Для випадку перетину двох нечіткої безлічі ∩ , заданої різними функціями приналежності, результат операції зображений на рис. 4.1, а, б. При цьому лінійні Z-образна і S-образна функції приналежності мають параметри a=3, b=6, а П-образні функції приналежності – а=1, b=3, c=4, d=7 і a=3, b=6, с=7, d=9 відповідно.

Рис 4.1. Графічне представлення операції перетину двох нечітких множин і , заданих лінійними Z-образної і S-образної функціями приналежності (а) і П-образними (б) функціями приналежності

Об'єднання. Об'єднанням двох нечітких множин і називається деяка третя нечітка множина , задана на цьому ж універсумі X, функція приналежності якого визначається за наступною формулою:

для будь-якого . (4.4)

Операція об'єднання нечітких множин по аналогії із звичайними множинами позначається знаком "∪". В цьому випадку результат операції об'єднання двох нечітких множин записується у вигляді: = ∪ .

Операцію об'єднання нечітких множин в сенсі (4.4) іноді називають max-об’єднанням або -об’єднанням. Останнє позначення пов'язане з визначенням логічної операції "АБО" (невиключного АБО), яка в математичній логіці позначається знаком " ". Відповідно функція приналежності об'єднання в цьому випадку часто записується у вигляді: для будь-якого . При цьому знак " " використовується як синонім операції максимуму. Оскільки в практиці нечіткого моделювання ця операція використовується найчастіше, надалі, кажучи про об'єднання нечітких множин, якщо явно не вказане інше, ми матимемо на увазі їх mах-об'єднання ( -об'єднання).

Як приклад розглянемо нечітку множину , яка, як і вище, представляє в деякому контексті "невелике натуральне число", і дорівнює: ={<1, 1.0>, <2, 1.0>, <3, 0.9>, <4, 0.8>, <5, 0.6>, <6, 0.5>, <7, 0.4>, <8, 0.2>, <9, 0.1>}, і нечітка множина , яка представляє "натуральне число, яке приблизно дорівнює двом", і дорівнює: ={<1, 0.5>, <2, 1.0>, <3, 0.6>, <4, 0.4>, <5, 0.2>, <6, 0>, <7, 0>, <8, 0>, <9, 0>}. Тоді нечітка множина як результат операції об'єднання ∪ буде дорівнювати: ={<1, 1.0>, <2, 1.0>, <3, 0.9>, <4, 0.8>, <5, 0.6> <6, 0.5>, <7, 0.4>, <8, 0.2>, <9, 0.1>}. Змістовно нечітка множина може представляти в цьому ж контексті "невелике натуральне число або натуральне число, яке приблизно дорівнює двом".

Результат операції об'єднання двох і більшої кількості нечітких множин, заданих на одному і тому ж універсумі X, можна зобразити графічно в декартовій системі координат на площині. Для випадку об'єднання двох нечітких множин і , заданих різними функціями приналежності, результат операції зображений на рис. 4.2, а, б.

Рис. 4.2. Графічне представлення операції об'єднання двох нечітких множин і , заданих лінійними Z-образною і S-образною функціями приналежності (а) і П-образними∪ (б) функціями приналежності

Різниця. Різницею двох нечітких множин і називається деяка третя нечітка множина , задана на цьому ж універсумі X, функція приналежності якого визначається за наступною формулою:

для будь-якого (4.5)

де знак мінус означає звичайну операцію арифметичної різниці двох чисел. Операція різниці двох нечітких множин по аналогії із звичайними множинами позначається знаком "\". В цьому випадку результат операції різниці двох нечітких множин можна записати у вигляді: = .

Так, якщо, як і вище, розглянути нечітку множину , яка дорівнює: ={<1, 1.0>, <2, 1.0>, <3, 0.9>, <4, 0.8>, <5, 0.6>, <6, 0.5>, <7, 0.4>, <8, 0.2>, <9, 0.1>}, і нечітка множина, яка дорівнює: ={<1, 0.5>, <2, 1.0>, <3, 0.6>, <4, 0.4>, <5, 0.2>, <6, 0>, <7, 0>, <8, 0>, <9, 0>}, то різниця буде дорівнювати: ={<1, 0.5>, <2, 0>, <3, 0.3>, <4, 0.4>, <5, 0.4>, <6, 0.5>, <7, 0.4>, <8, 0.2>, <9, 0.1>}.

Змістовно нечітка множина може бути в тому ж контексті "невеликим натуральним числом, що не є приблизно рівним двом". Для цих же двох нечітких множин різниця буде дорівнювати порожній множині, оскільки всі значення функції приналежності результату будуть дорівнювати нулю. Змістовно нечітка множина може представляти в тому ж контексті "натуральне число, яке приблизно дорівнює двом і, що не є невеликим".

Результат операції різниці двох нечітких множин і , заданих на одному і тому ж універсумі X різними функціями приналежності, зображений на мал. 4.3, а, б.

Рис. 4.3. Графічне представлення операції різниці двох нечітких множин і , заданих лінійними Z-образною і S-образною функціями приналежності (а) і П-образними (б) функціями приналежності

Симетрична різниця. Слід відмітити, що операція різниці двох нечітких множин на відміну від операцій -об’єднання і -перетину не є комутативною. За аналогією із звичайними множинами іноді виявляється корисною операція симетричної різниці двох нечітких множин і (позначатимемо її через ). За визначенням:

для будь-якого , (4.6)

де в правій частині виразу застосовується операція модуля (або обчислення абсолютного значення) числа. При цьому виявляється справедливим наступне твердження: = тобто симетрична різниця двох нечітких множин є об'єднанням двох різниць нечітких множин і .

Якщо, як і вище, розглянути нечітку множину , яка дорівнює: ={<1, 1.0>, <2, 1.0>, <3. 0.9>, <4, 0.8>, <5, 0.6>, <6, 0.5>, <7, 0.4>, <8, 0.2>, <9, 0.1>} та нечітку множину , яка дорівнює: ={<1, 0.5>, <2, 1.0>, <3, 0.6>, <4, 0.4>, <5, 0.2>, <6, 0>, <7, 0>, <8, 0>, <9, 0>}, то їх симетрична різниця буде дорівнювати: ={<1, 0.5>, <2, 0>, <3, 0.3>, <4, 0.4>, <5, 0.4>, <6, 0.5>, <7, 0.4>, <8, 0.2>, <9, 0.1>}. В цьому випадку результат співпадатиме із звичайною різницею .

Операція симетричної різниці двох нечітких множин і , заданих на одному і тому ж універсумі X різними функціями приналежності, може бути проілюстрована графічно (рис. 4.4). При цьому результату операції симетричної різниці нечітких множин також відповідає темніша область на графіці.

Рис. 4.4. Графічне представлення операції симетричної різниці двох нечітких множин і , заданих лінійними Z-образною і S-образною функціями приналежності (а) і П-образними (б) функціями приналежності

Доповнення. Спеціально слід зупинитися на унарній операції доповнення нечіткої множини. Доповнення нечіткої множини позначається через і визначається як нечітка множина ={x| }, функція приналежності якої визначається за наступною формулою:

для будь-якого (4.6)

Якщо, як і вище, розглянути нечітку множину , яка дорівнює: ={<1, 1.0>, <2, 1.0>, <3, 0.9>, <4, 0.8>, <5, 0.6>, <6, 0.5>, <7, 0.4>, <8, 0.2>, <9, 0.1>}, і нечітка множина , яка дорівнює: ={<1, 0.5>, <2, 1.0>, <3, 0.6>, <4, 0.4>, <5, 0.2>, <6, 0>, <7, 0>, <8, 0>, <9, 0>}, то їх доповнення будуть дорівнювати: ={<1, 0>, <2, 0>, <3, 0.1>, <4, 0.2>, <5, 0.4>, <6, 0.5>, <7, 0.6>, <8, 0.8>, <9, 0.9>} і ={<1, 0.5>, <2, 0>, <3, 0.4>, <4, 0.6>, <5, 0.8>, <6, 1.0>, <7, 1.0>, <8, 1.0>, <9, 1.0>}. Змістовно нечітка множина може представляти в даному контексті "натуральне число, не що є невеликим", а нечітка множина – "натуральне число, яке не рівне приблизно двом".

Операція доповнення нечіткої множини може бути проілюстрована графічно (рис. 4.5). Як неважко бачити, графік функції приналежності доповнення нечіткої множини симетричний графіку функції приналежності початкової нечіткої множини щодо лінії: y=0.5.

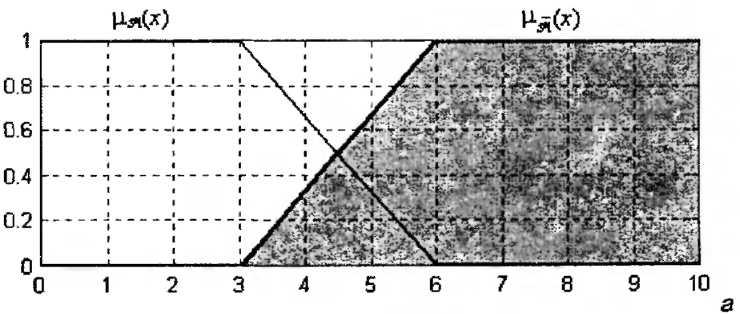
Рис. 4.5. Графічне представлення операції доповнення нечіткої множини , яка задана лінійною Z-образною (а) функцією приналежності і П-образною (б) функцією приналежності

Особливість даних операцій над нечіткими множинами полягає в тому, що для них не виконуються закон виключеного третього і закон тотожності (властивості доповнюваності операцій перетину і об'єднання). А саме, в загальному випадку є справедливими такі нерівності:

, (3.17)

. (3.18)