Міністерство освіти і науки України

Харківський національний університет радіоелектроніки

КОНСПЕКТ ЛЕКЦІЙ

з дисципліни

"НЕЧІТКІ МНОЖИНИ"

для підготовки магістрів усіх форм навчання

спеціальності 122 − Комп’ютерні науки

галузі знань 12 − Інформаційні технології

Електронне видання

Затверджено

кафедрою "Штучного інтелекту"

Протокол № ___ від "__" __________ 2018 р.

Харків 2018

Конспект лекцій з дисципліни "Нечіткі множини" для підготовки фахівців освітньо-кваліфікаційного рівня магістр за спеціальністю 122 – Комп’ютерні науки [Електронне видання] / Упоряд. К.Е. Петров. – Харків: ХНУРЕ, 2018 – 128 с.

Упорядник К.Е. Петров

Зміст

Вступ………………………………………………………………………...	4
Тема 1. Основні поняття теорії нечітких множин.…….…………...….…	6
Тема 2. Операції над нечіткими множинами……….……….……………	30
Тема 3. Нечіткі відношення, відображення…….…………………….......	40
Тема 4. Нечіткі величини, числа, та інтервали…………………….…......	57
Тема 5. Основи нечіткої логіки………………….………………………...	75
Тема 6. Продукційні нечіткі моделі…………………..…………….……..	88
Тема 7. Алгоритми нечіткого логічного виведення……………………...	108
Тема 8. Методи нечіткої кластеризації………………….………….……..	117
Бібліографічний список ………….…………………..…………………….	126

Вступ

Історія нечітких множин починається з 1965 р., коли професор Заде (Zadeh) з Каліфорнійського університету в Берклі опублікував статтю «Fuzzy Sets» в журналі «Information and Control». Прикметник «fuzzy», який переводиться як «нечіткий», «розмитий», «ворсистий», «пухнастий», введено в назву нової теорії, щоб дистанціювати її від традиційної чіткої математики і аристотелевої логіки, що оперують з чіткими поняттями «Належить – не належить», «істина – хибність». Поняття нечіткої множини – ця спроба формалізації лінгвістичної інформації для побудови математичних моделей. У основі цього поняття лежить уявлення про те, що елементи, які складають дану множину і володіють загальною властивістю, можуть володіти їй в різній ступені і, отже, належати до цієї множини з різним ступенем. При такому підході вислови типу «такий-то елемент належить даній множині» втрачають сенс, оскільки необхідно вказати, наскільки сильно або з яким ступенем елемент задовольняє властивостям множини.

Початком практичного застосування теорії нечітких множин вважають 1973 р., коли Мамдані (Mamdani) і Ассиліан (Assilian) з Лондонського коледжу Королеви Мері побудували перший нечіткий контролер для лабораторної моделі парового двигуна. Концепцію першого нечіткого контролера складають ідеї нечіткого логічного виводу і нечіткого алгоритму, викладені Заде в 1973 р. Перший промисловий нечіткий контролер запрацював в кінці 1970-х років в Данії – Холмблад (Holmblad) і Остергард (Ostergaard) впровадили нечітку логіку в управління процесом випалення цементу. У 1980-х роках європейські і американські інженерні і наукові співтовариства вельми скептично сприйняли нову теорію. Зате на Сході нечітка логіка пішла «на ура». Для людей, вихованих на східній філософії, з її неоднозначними і розпливчатими категоріями, нечітка логіка відразу стала своєю, рідною.

У Японії перший нечіткий контролер розробив Сугено (Sugeno) в 1983 р. за замовленням фірми Fuji El. для системи очищення води. Чотири роки опісля фірма Hitachi розробила нечітку систему управління рухом електропоїзду в метро м. Сендай. На 1990 р. в Японії було зареєстровано 30 патентів, пов'язаних з нечіткою логікою. На початку 1990-х років японці поставили нечітку логіку «на конвеєр» – почалося серійне виробництво побутових приладів з нечітким управлінням: камери з автоматичним фокусуванням (Canon), кондиціонери повітря (Mitsubishi), пральні машини (Panasonic і Matshushita).

Тоді ж фірми Honda і Nissan розробили автоматичну трансмісію з нечітким управлінням, а фірма Toshiba – нечіткий контроллер ліфту. Нечітка логіка стає маркетинговою зброєю на японському ринку – fuzzy-товари розкуповуються швидше.

У 1994 р. Коско (Kosko) довів теорему про нечітку апроксимацію, згідно якої, будь-яка математична система може бути апроксимована системою на нечіткій логіці. Отже, за допомогою природно-мовних висловів <Якщо – то>, з подальшою їх формалізацією засобами теорії нечітких множин, можна скільки завгодно точно відобразити довільний взаємозв'язок «входи – вихід» без використання складного апарату диференціального і інтегрального числень, що традиційно використовується в управлінні та ідентифікації. Практичні успіхи нечіткого управління отримали теоретичне обґрунтування.

Сьогодні нечітка логіка розглядається як стандартний метод моделювання і проектування. У 1997 р. мова нечіткого управління (Fuzzy Control Language) внесена до Міжнародного стандарту програмованих контролерів IЕС 1131-7. Системи на нечітких множинах розроблені і успішно упроваджені в таких областях, як: медична діагностика, технічна діагностика, фінансовий менеджмент, управління персоналом, біржове прогнозування, розпізнавання образів, розвідка копалин, виявлення шахрайств, управління комп'ютерними мережами, управління технологічними процесами, управління транспортом, логістика, пошук інформації в Інтернеті, радіозв'язок і телебачення. Спектр додатків дуже широкий – від побутових відеокамер, пилососів і пральних машин до засобів наведення ракет ППО і управління бойовими вертольотами і літаками. Як і раніше лідирує Японія, в якій випущено понад 4800 «нечітких» патентів (для порівняння, в США їх близько 1700). Практичний досвід розробки систем на нечітких множинах свідчить, що терміни і вартість їх проектування значно нижчі, ніж при використанні традиційного математичного апарату, при цьому забезпечуються необхідні рівні якості. Отець нечіткої логіки Лотфі Заде якось із цього приводу відмітив, що «майже завжди можна зробити такий же самий продукт без нечіткої логіки, але з нечіткою буде швидше і дешевше».

Тема 1. Основні поняття теорії нечітких множин

1. Основні терміни і визначення

Визначення 1.1. Нечіткою множиною (fuzzy set) є сукупність елементів довільної природи, щодо яких не можна з повною визначеністю стверджувати, – чи належить той або інший елемент цієї сукупності даній множині чи ні. Іншими словами, нечітка множина відрізняється від звичайної множини тим, що для всіх або частини його елементів не існує однозначної відповіді на питання: "Належить або не належить той або інший елемент даній нечіткій множині?" Можна це питання поставити і по-іншому: "Володіють чи ні його елементи деякою характеристичною властивістю, яка може бути використане для завдання цієї "нечіткої множини?"

Для побудови нечітких моделей систем само поняття нечіткої множини слід визначити більш строго, щоб виключити неоднозначність тлумачення тих або інших її властивостей. Виявилось, що існують декілька варіантів формального визначення нечіткої множини, які по суті відрізняються між собою способом завдання характеристичній функції даних множин. Серед цих варіантів найбільш природним і інтуїтивно зрозумілим є завдання області значень подібної функції як інтервал дійсних чисел, які знаходяться між 0 і 1 (включаючи і самі ці значення).

Визначення 1.2. (Математичне визначення нечіткої множини). Формальна нечітка множина визначається як множина впорядкованих пар або кортежів виду: , де x є елементом деякої універсальної множини або універсуму X, – функція приналежності, яка ставить у відповідність кожному з елементів деяке дійсне число з інтервалу [0,1], тобто дана функція визначається у формі відображення:

. (1.1)

При цьому значення для деякого означає, що елемент х безумовно належить нечіткій множині, а значення означає, що елемент безумовно не належить нечіткій множині .

Формальна кінцеву нечітку множину будемо записувати у вигляді:

а загальному випадку – у вигляді:

Окрім прийнятих нами позначень кінцеві нечіткі множини часто записуються у формі:

У разі безперервної множини X використовують таке позначення:

При цьому коса і горизонтальна риса служать просто роздільником, а знак "+" позначає не арифметичну суму, а теоретико-множинне об'єднання окремих елементів. Знаки і означають сукупність пар та .

Оскільки існуючі відмінності у формах запису не мають принципового значення, в подальшому тексті нечіткі множини для зручності позначатимуться із знаком тильда "~" вгорі:, , , , . З іншого боку, для запису класичних (не нечітких, crisp) множин будуть як і раніше використовуватися загальноприйняті позначення у формі: А, В, З, D.

Зі всіх нечітких множин виділимо два окремі випадки, які по суті співпадають зі своїми класичними аналогами і використовуються надалі при визначенні інших нечітких понять. У теорії нечітких множин зберігають свій сенс деякі спеціальні класичні множини.

Визначення 1.3. Так, наприклад, порожня нечітка множина або множина, яка не містить жодного елементу, як і раніше позначається через і формально визначається як така нечітка множина, функція приналежності якої тотожно дорівнює нулю для всіх без виключення елементів: .

Визначення 1.4. Що стосується іншої спеціальної множини, то так званий універсум, що позначається через X, вже був використаний вище як звичайна множина, що містить в рамках деякого контексту всі можливі елементи. Формально зручно вважати, що функція приналежності універсуму як нечіткої множини тотожно дорівнює одиниці для всіх без виключення елементів: .

Як не важко помітити, розглянуті поняття порожньої множини і універсуму, що використовуються в теорії нечітких множин, за своїм змістом повністю ідентичні відповідним поняттям класичної теорії множин. Тому кажучи про них, ми не використовуватимемо визначення "нечітке", оскільки в довільному контексті вони завжди є формально визначеними.

Для того, щоб визначити кінцеві і нескінченні нечіткі множини, необхідно ввести в розгляд одне з основних понять, яке використовується для характеристики довільної нечіткої множини, а саме – поняття носія нечіткої множини.

Визначення 1.5. Носієм нечіткої множини називається звичайна множина, яка містить ті і лише ті елементи універсуму, для яких значення функції приналежності відповідної нечіткої множини відмінні від нуля. Математично носій нечіткої множини визначається наступною умовою:

(1.2)

Іноді носій нечіткої множини позначають через supp{ ), де supp – перші букви англійського слова support.

Очевидно, порожня нечітка множина має порожній носій, оскільки для будь-якого його елементу. Для зручності і скорочення запису довільної нечіткої множини часто указують лише значення її функції приналежності для елементів носія, неявно припускаючи, що решта всіх значень функції приналежності дорівнює нулю.

Залежно від кількості елементів в нечіткій множині по аналогії із звичайними множинами можна визначити скінченні і нескінченні нечіткі множини.

Зручно рахувати потужність порожньої множини рівної 0.

Визначення 1.6. Аналогічним чином можна визначити і нескінченні нечіткі множини як такі нечіткі множини, носій яких не є скінченною множиною. При цьому зліченою нечіткою множиною називатимемо нечітку множину зі зліченим носієм, тобто носій якого має злічену потужність N₀ в звичайному сенсі. Незліченою нечіткою множиною називатимемо нечітку множину з незліченним носієм, тобто носій якого має незліченну потужність або потужність континууму с (або N) в звичайному сенсі.

Очевидно, дане вище визначення носія нечіткої множин коректно, оскільки як для скінченних, так і для нескінченних нечітких множин вираз (1.2) має сенс.

Щоб привести деякі приклади нечітких множин і приступити до визначення їх основних властивостей, слід розглянути основні способи, якими формально можуть бути задані довільні нечіткі множини.

Нечіткі множини можуть бути задані двома основними способами:

1. У формі списку з явним перерахуванням всіх елементів і відповідних ним значень функції приналежності, утворюючих дану нечітку множину. При цьому часто елементи з нульовими значеннями функції приналежності просто не вказуються в даному списку. Цей спосіб підходить для завдання нечітких множин з кінцевим дискретним носієм і невеликим числом елементів. В цьому випадку нечітку множину зручно записувати у вигляді:

де n – дане число елементів нечіткої множини (його носія).

Наприклад, візьмемо за універсум Х={1, 2, 3...} – множину натуральних чисел. Тоді нечітка множина, що представляє в деякому контексті "невелике натуральне число", можна задати таким чином: = {<1, 1.0>, <2, 1.0>, <3, 0.9>, <4, 0.8>, <5, 0.6>, <6, 0.5>, <7, 0.4>, <8, 0.2>, <9, 0.1>}. При цьому елементи, для яких , відсутні в цьому списку.

2. Аналітично – у формі математичного виразу для відповідної функції приналежності. Цей спосіб може бути використаний для завдання довільних нечітких множин, як з скінченним, так і з нескінченним носієм. В цьому випадку нечітку множину зручно записувати у вигляді: , де – деяка функція, що задана аналітично у формі математичного виразу f(x) або графічно у формі деякої кривої.

Для формальної строгості при завданні нечітких множин необхідно явно указувати відповідний універсум X елементів, з яких формується те або інша конкретна нечітка множина. У загальному випадку ніяких припущень щодо елементів цієї множини не робиться. Проте з практичної точки зору доцільно обмежити універсум елементами даної предметної області або вирішуваного завдання. Оскільки при побудові нечітких моделей систем використовуються кількісні змінні, то найчастіше, як універсум X використовується деяка підмножина дійсних чисел, наприклад, множина ненегативних дійсних чисел + або натуральних чисел .

Розглянемо деякі конкретні приклади нечітких множин.

Приклад 1.1. Припустимо, необхідно побудувати деяку нечітку множину, яка змістовно описувала б вихідні (неробочі) дні звичайного семиденного тижня. У термінології класичних множин ситуація тривіальна, а саме, дні тижня з понеділка по п'ятницю є робочими, а субота і неділя – вихідними. Зауважимо, що мова йде про традиційний календарний тиждень, а робочі дні вважаються без урахування змінності і інших особливостей трудовитрат. Таким чином, звичайна не нечітка множина вихідних днів А складається з двох елементів: А={субота, неділя}. Ця точка зору є загальноприйнятою для бухгалтерії при розрахунку заробітної платні співробітникам.

Що ж до визначення відповідної нечіткої множини , спробуємо суб'єктивно оцінити ступінь нашого емоційного відношення до різних днів тижня, розглядаючи їх з погляду вихідних і психології можливого відпочинку. Для більшості з нас ситуація вже не здаватиметься такою простою, як у попередньому випадку.

Що стосується днів з понеділка по четвер, то відношення до них як до робочих днів навряд чи зміниться. А ось п'ятниця, особливо її вечір для багатьох асоціюється з повноцінним відпочинком і високим ступенем позитивних емоцій. Субота є, безумовно, вихідним днем, протягом якого можуть бути забуті всі службові турботи, особливо в суботу увечері, а для багатьох – і вночі. А ось що стосується неділі, то ближче до вечора ситуація міняється – нерідко на розум приходить думка: "Завтра потрібно рано вставати і приступати до роботи", і настрій вже не можна вважати таким безхмарним.

Таким чином, дана нечітка множина , що описує вихідні дні тижня, може бути задана, наприклад, у вигляді: ={<понеділок, 0>, <вівторок, 0>, <середа, 0>, <четвер, 0>, <п'ятниця, 0.5>, <субота, 1.0>,<неділя, 0.8>}. Тут в якості універсуму виступають всі дні тижня: Х={понеділок, вівторок, середа, четвер, п'ятниця, субота, неділя}, а функція приналежності задається перерахуванням своїх значень. При цьому чим ближче її значення до 1, тим більше відповідає той або інший день тижня нашому відношенню до нього як до вихідного дня.

Спробуємо представити цю нечітку множину графічно. Зобразимо графічно функцію приналежності цієї нечіткої множини. Для цього на горизонтальній вісі відзначимо окремі значення елементів універсуму (у нашому випадку – елементи множини X), а на вертикальній осі – значення відповідної функції приналежності (рис. 1.1).

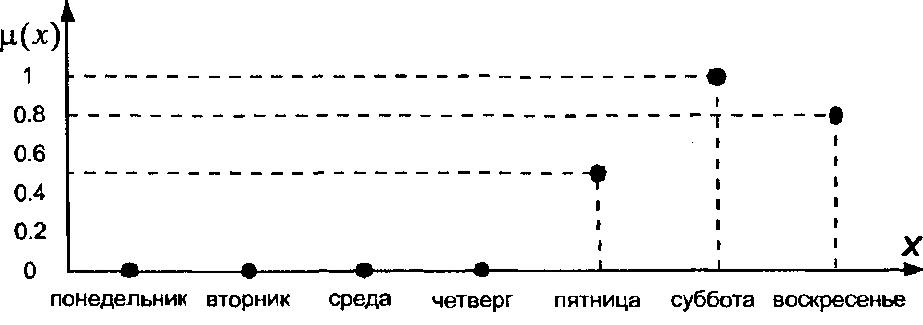
Рис. 1.1. Графічне представлення скінченної нечіткої множини, що описує вихідні дні тижня, у формі значень функції приналежності цієї нечіткої множини

Навіть цей простий приклад показує, що однозначно визначити ту або іншу нечітку множину не представляється можливим, а іноді – і принципово неможливим. Якщо хтось вирішить, що його суб'єктивна оцінка вихідних днів відрізняється від розглянутої вище, то він буде по-своєму правий. Відповідно, у якості нечіткої множини могли б виступати множини: ={<понеділок, 0>, <вівторок, 0>, <середа, 0>, <четвер, 0.1>, <п'ятниця, 0.6>, <субота, 1.0>, <неділя, 0.7>} або ={<понеділок, 0>, <вівторок, 0.1>, <середа, 0> <четвер, 0.1>, <п'ятниця, 0.5>, <субота, 0.9>, <неділя, 0.8>}. Важливо уявляти собі, що з формальної точки зору всі вони повинні задовольняти лише початковому визначенню нечіткої множини у формі (1.1).

Продовжимо розгляд попереднього прикладу з метою його розширення на випадок нескінченної нечіткої множини. Оскільки наше відношення до вихідних днів тижня може змінюватися протягом часу доби, а горизонтальна вісь на рис. 1.1 легко перетворюється у безперервну вісь часу, то і відповідна нечітка множина допускає природне узагальнення. А саме, кожен з днів тижня представлятимемо як окрему добу з переходом о 0 годині до наступного дня тижня. Тоді функція приналежності нечіткої множини може бути задана аналітично у формі деякої кривої, яка в максимально нашому емоційному відношенню до вихідних днів протягом всієї доби.

Один з можливих варіантів такої функції приналежності зображений на рис. 1.2, на якому горизонтальна вісь відповідає добовому представленню семиденного тижня.

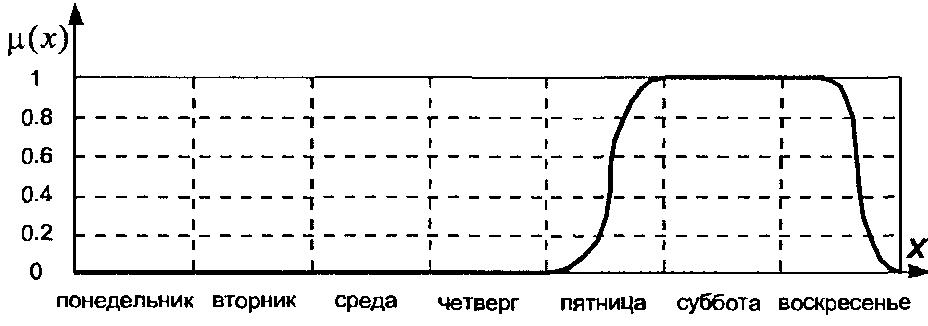
Рис. 1.2. Графічне представлення нескінченної нечіткої множини, що описує вихідні дні тижня, у формі кривій його функції приналежності

Для порівняння розглянемо представлення звичайної (не нечіткої) множини вихідних днів тижня A={субота, неділя} у формі нескінченної множини. В цьому випадку характеристична функція даної множини може бути записана у вигляді кусочно-безперервної функції, що приймає тільки два значення, – 0 і 1 на множині значень універсуму X (рис. 1.3).

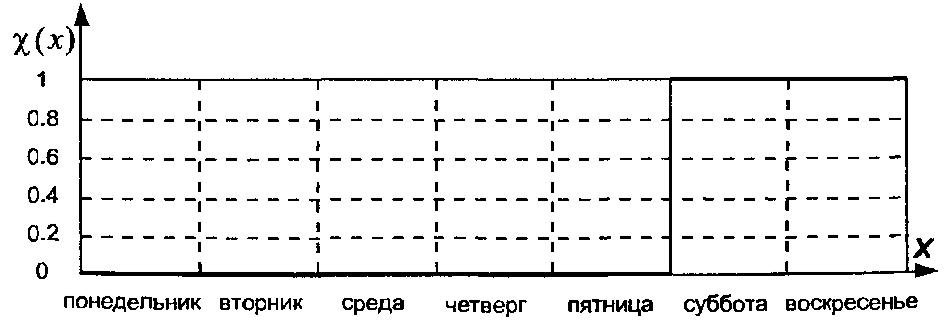
Рис. 1.3. Графічне представлення звичайної множини вихідних днів А у формі значень відповідної характеристичної функції

З розгляду даного прикладу видно, що характеристичну функцію звичайної множини А в тому або іншому контексті зручно вважати спеціальним випадком функції приналежності відповідної нечіткої множини . Цей факт дозволяє розглядати довільну нечітку множину як узагальнення звичайної множини А, а множина А – як звуження або окремий випадок відповідної нечіткої множини .

Приклад 1.2. В якості другого прикладу розглянемо типову побутову ситуацію, з якою стикається багато хто з нас при спробі дати характеристику температури того або іншого напою. Подібна характеристика зазвичай грунтується виключно на суб'єктивних відчуттях, наприклад, гаряча кава або чай, холодний квас або кола. Стосовно цієї ситуації розглянемо нечітку множину, яке характеризуватиме "гарячу каву". В цьому випадку в якості універсуму природно узяти шкалу температури, виміряної в градусах Цельсія і поміщеної у відкритий інтервал (0°С, 100°С), тобто Х={х | 0°С <x< 100°С}. Вибір цього інтервалу цілком виправданий з фізичної точки зору, оскільки саме в цьому діапазоні температур кава потенційно може існувати як напій. Очевидно, що окрема чашка кави, скажемо x1, з температурою 10°С не може бути визнана гарячою, тому для неї значення функції приналежності даній множині дорівнюватиме нулю, тобто . З іншого боку інша чашка кави x2 з температурою 90°С цілком може бути визнана гарячою, тому для неї значення функції приналежності даній множині дорівнюватиме 1, тобто .

Що стосується значень температур, які знаходяться між цими крайніми значеннями, то ситуація представляється вже не такою однозначною. Більш того, вона за своєю суттю є виключно суб'єктивною і невизначеною, оскільки чашка кави з температурою 55°С для одного індивідуума може опинитися гарячою, а для іншого – не дуже гарячою. Саме в цьому і проявляється нечіткість завдання відповідної множини. Проте, ми можемо бути цілком упевнені в загальному вигляді функції приналежності, а саме – в тому, що відповідна функція приналежності є такою, що монотонно зростає (або більш строго – монотонно неубувує).

Таким чином, в якості множини, що описує гарячу каву, можна розглядати, наприклад, таку нечітку множину, для якої функція приналежності має наступний вигляд (див. рис. 1.4, а або 1.4, б).

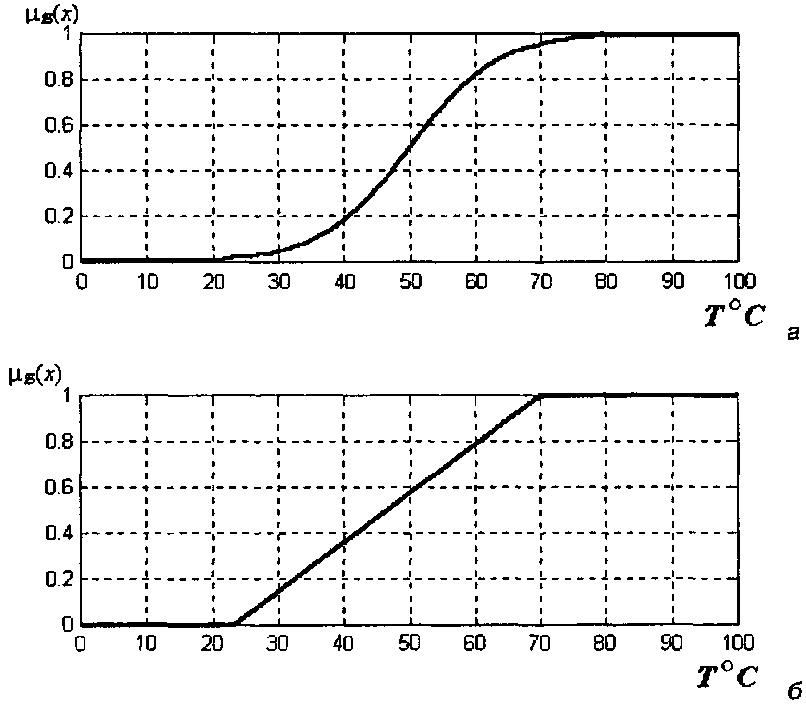
Рис. 1.4. Графіки варіантів функцій приналежності для нечіткої множини, що описує "гарячу каву"

Розглянутий приклад допускає узагальнення на інші ситуації, пов'язані з представленням аналогічної нечіткої інформації. Зокрема, цілий ряд властивостей технічних пристроїв, побутових приладів і соціальних явищ можуть ініціювати схожі нечіткі множини. Наприклад, такі фрази, як "швидкісний автомобіль", "високооплачувана робота", "упорядкована квартира", "щедрі чайові", "престижний район", "смачна вечеря" породжують нечіткі множини, аналогічні тим, що розглянуті в прикладі 1.2. При цьому загальний вигляд функцій приналежності таких множин буде подібний зображеним на рис. 1.4, а, б.

Приклад 1.3. Наступний приклад пов'язаний з розпізнаванням букв деякого алфавіту і десяткових цифр, що є вельми актуальним завданням при скануванні текстових документів. Припустимо, є деяке графічне зображення, на якому представлені деякі буква і цифра (рис. 1.5).

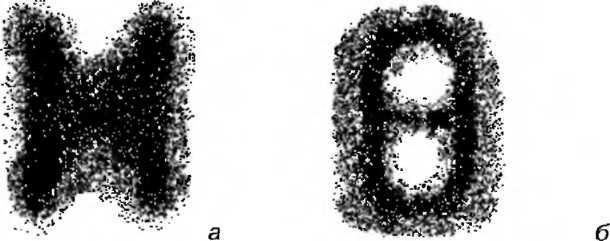
Рис. 1.5. Графічне зображення деякої букви (а) і деякої десяткової цифри (б)

Перше зображення породжує на множині усіх прописних букв (наприклад, українського) алфавіту X={А, Б, В..., Я} деяку скінченну нечітку множину ={<А, (А) >, <Б, (Б) >,..., <Я, (Я) >}. Ця нечітка множина змістовно описує відповідність зображення, представленого на рис. 1.5, а, тій або іншій букві алфавіту. Такою множиною може бути, наприклад наступна нечітка множина: ={<А, 0>, <Б, 0>...,<И, 1.0>, <Й, 0.9>, <К, 0.4>, <Л, 0>, <М, 1.0>, <Н, 1.0>, <О, 0>...,<Х, 0.3>,...,<Я, 0>}. Пропущені елементи відповідають нульовим значенням функції приналежності для решти букв алфавіту.

Друге зображення породжує на множині всіх десяткових цифр Х={0, 1, 2, 3, 4, 5, 6, 7, 8, 9} скінченну нечітку множину ={<0 (0) >, <1 (1)>,..., <9 (9))>}. Ця нечітка множина змістовно описує відповідність зображення, представленого на рис. 1.5, б, тій або іншій десятковій цифрі. У окремому випадку такою нечіткою множиною може бути, наприклад, наступна: ={<0, 0.8>, <1, 0>, <2, 0>, <3, 0.9>, <4, 0>, <5, 0.2>, <6, 1.0>, <7, 0>, <8, 1.0>, <9, 0.9>}. Тут вказані всі значення функції приналежності для елементів універсуму.

Розглянуті вище приклади ілюструють характерні аспекти невизначеності, які зустрічаються в практиці нечіткого моделювання. По-перше, кожна з нечітких множин допускає в загальному випадку неоднозначне представлення, що відображає суб'єктивну точку зору на моделювання відповідних практичних ситуацій. Іншими словами, якщо хтось не згоден з конкретним варіантом завдання нечітких множин , і , то він може запропонувати свої варіанти значень функцій приналежності. І формально по-своєму будуть праві, оскільки адекватність цих представлень обумовлюється їх подальшим практичним використанням для вирішення того або іншого завдання. По-друге, ці приклади добре ілюструють концептуальну відмінність між теорією нечітких множин і теорією ймовірності, оскільки розглянуті варіанти невизначеності мають не стохастичний характер. І, нарешті, по-третє, вибір аналітичної функції або вигляду кривої для тієї або іншої функції приналежності з метою завдання відповідної нечіткої множини часто визначається міркуваннями зручності і простоти.

Перейдемо до розгляду основних характеристик нечітких множин, які використовуються для їх детальнішого опису і систематичного вивчення.