
- •Содержание
- •Предисловие
- •Принятые обозначения
- •Глава 1. Упругие волны
- •§ 1.1. Уравнение волны
- •§ 1.2. Волновые уравнения
- •§ 1.3. Скорость упругих волн
- •§ 1.4. Энергия упругой волны
- •§ 1.5. Стоячие волны
- •§ 1.6. Звуковые волны
- •§ 1.7. Эффект Доплера для звуковых волн
- •Задачи
- •Глава 2. Электромагнитные волны
- •§ 2.1. Волновое уравнение электромагнитной волны
- •§ 2.2. Плоская электромагнитная волна
- •§ 2.3. Стоячая электромагнитная волна
- •§ 2.4. Энергия электромагнитной волны
- •§ 2.5. Импульс электромагнитной волны
- •§ 2.6. Эффект Доплера для электромагнитных волн
- •§ 2.7. Излучение диполя
- •Задачи
- •Глава 3 Вступление
- •§ 3.1. Световая волна
- •§ 3.2. Электромагнитная волна на границе раздела
- •§ 3.3. Геометрическая оптика
- •§ 3.4. Фотометрические величины
- •Задачи
- •Глава 4 Интерференция света
- •§ 4.1. Интерференция световых волн
- •§ 4.2. Когерентность
- •§ 4.3. Интерференционные схемы
- •§ 4.5. Интерферометр Майкельсона
- •§ 4.6. Многолучевая интерференция
- •Задачи
- •Глава 5 Дифракция света
- •§ 5.1. Принцип Гюйгенса–Френеля
- •§ 5.2. Дифракция Френеля от круглого отверстия
- •§ 5.4. Дифракция Фраунгофера
- •§ 5.6. Дифракция Фраунгофера от щели
- •§ 5.7. Дифракционная решетка
- •§ 5.8. Дифракционная решетка как спектральный прибор
- •§ 5.9. Дифракция от пространственной решетки
- •§ 5.10. О голографии
- •Задачи
- •Глава 6 Поляризация света
- •§ 6.1. Общие сведения о поляризации
- •§ 6.3. Поляризация при двойном лучепреломлении
- •§ 6.4. Суперпозиция поляризованных волн
- •§ 6.5. Интерференция поляризованных волн
- •§ 6.6. Искусственное двойное лучепреломление
- •§ 6.7. Вращение направления линейной поляризации
- •Задачи
- •Глава 7 Взаимодействие света с веществом
- •§ 7.1. Дисперсия света
- •§ 7.2. Классическая теория дисперсии
- •§ 7.3. Групповая скорость
- •§ 7.4. Поглощение света
- •§ 7.5. Рассеяние света
- •Задачи
- •Приложения
- •1. Поведение плоской волны на границе двух диэлектриков
- •3. Излучение Вавилова–Черенкова
- •4. Единицы физических величин
- •5. Десятичные приставки к названиям единиц
- •6. Греческий алфавит
- •7. Единицы величин в СИ и системе Гаусса
- •9. Некоторые физические константы

16 |
Глава 1 |
|
|
страняющейся в произвольном направлении, как было отмечено на с. 11 под формулой (1.12 ), фазовая скорость в направлении оси X равна v/cos . Тогда волновые уравнения вдоль осей X, Y, Z будут иметь следующий вид
2 |
|
cos2 |
2 |
, |
2 |
|
cos2 2 |
, |
2 |
|
cos2 |
|
2 |
, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x2 |
v2 |
|
|
t 2 |
y2 |
v2 t |
2 |
z |
2 |
v2 |
|
t 2 |
||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
где , , — углы между волновым вектором k и осями координат. Сложив отдельно левые и правые части этих уравнений и учитывая, что
cos2 + cos2 + cos2 1,
мы и приходим к уравнению (1.23), где, напомним, v /k. Отметим, что выражения для сферических и цилиндрических волн
также являются решением волнового уравнения (1.23), надо только
2
вторые производные по координатам, т. е. D — оператор Лапласа — записать в соответствующей системе координат (сферической или цилиндрической).
Волновые уравнения (1.21) и (1.23) играют весьма важную роль в теории волновых процессов. Если мы, исходя из законов механики при изучении некоторого явления, придем, например, к уравнению вида (1.23), то сразу можно утверждать, что имеем дело с волновым процессом, скорость распространения v которого легко найти из сопоставления полученного уравнения с (1.23). В дальнейшем мы этим и воспользуемся.
§ 1.3. Скорость упругих волн
Скорость волны в тонком стержне. Под тонким имеется в виду стержень, толщина которого мала по сравнению с длиной волны . При малых продольных деформациях стержня справедлив закон Гука:
! = E , |
(1.24) |
где ! — напряжение (Н/м2), Е — модуль Юнга (Па), = / x. Заметим, что !, как и , величина алгебраическая, и знаки ! ивсегда одинаковы: при растяжении — положительные, при сжатии — отрицательные.

Упругие волны |
17 |
|
|
Рис. 1.4
Рассмотрим малый элемент стержня x I в момент, когда при прохождении волны он оказался, например, в растянутом состоянии (рис. 1.4). Применим к этому элементу 2-й закон Ньютона:
где — плотность материала стержня, S — площадь его поперечного сечения. В данный момент, как видно из рисунка, Fx(x + x) > 0, а Fx(x) < 0. Соответствующие же значения ! в сечениях х и х + х положительные (растяжение!). Поэтому правую часть уравнения можно переписать так:
!
Fx (x x) Fx (x) S!(x x) S!(x) S x, x
где учтено, что слева Fx и ! имеют разные знаки (это будет и при сжатии). Тогда##уравнение движения после сокращения наx S примет вид !/ x. Остается учесть (1.24), после чего получим окончательно:
|
2 |
E |
2 |
|
||
|
|
|
. |
(1.25) |
||
t2 |
x2 |
|||||
Мы пришли, таким образом, к волновому уравнению. Это позволяет утверждать, что в стержне будет распространяться продольная волна, скорость v которой легко определить, сопоставив полученное выражение с (1.23):
v |
E/ |
. |
(1.26) |
Заметим, что для не тонкого стержня выражение для v имеет более сложный вид и значение v оказывается больше, чем в случае тонкого стержня.
Можно показать, что скорость поперечных упругих волн в неограниченной изотропной твердой среде
v |
G/ |
, |
(1.27) |
где G — модуль сдвига среды, — ее плотность.

18 Глава 1
|
F |
|
2
1
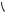


F
0 |
x x+dx |
X |
Рис. 1.5
Скорость волны в гибком шнуре. Найдем уравнение малых поперечных колебаний натянутого шнура, исходя из основного уравнения динамики. На малый элемент 12 шнура (рис. 1.5) слева действует сила натяжения F. Ее вертикальная проекция F (x) F sin . При малых смещениях sin = tg = / x, и мы можем записать
F (x) = –F / x.
Аналогичное выражение для проекции силы (только со знаком «+») можно записать и для правого конца элемента 12. Результирующая этих двух проекций сил
|
|
|
|
|
|
|
|
|
||||
F |
|
|
|
F |
|
|
|
|
F |
|
dx. |
(1.28) |
|
x 2 |
|
|
x 1 |
|
x |
x |
|
||||
Пренебрегая изменением силы F вдоль шнура (это справедливо для малых смещений при колебаниях), правую часть предыдущего выражения можно переписать так: F( 2 / x2)dx. Если ли-
нейная плотность шнура (масса единицы его длины) равна |
, |
||||||||
|
|
|
|
|
|
|
## |
1 |
|
то по второму закону Ньютона dx F dx, или |
|
||||||||
|
|
|
|
|
1 |
|
x |
|
|
|
2 |
|
F |
|
2 |
. |
(1.29) |
||
|
t2 |
|
1 |
|
x2 |
||||
|
|
|
|
|
|
||||
Из сравнения с (1.23) находим выражение для скорости волны в шнуре:
v |
F/ 1 |
. |
(1.30) |
Скорость звука в жидкостях и газах. Формулу (1.26) можно использовать для вычисления скорости продольных волн в жидкостях и газах. Действительно, вырезав мысленно канал в на-

Упругие волны |
19 |
|
|
правлении распространения плоской волны, мы можем повторить все рассуждения, приведшие нас к этой формуле. Остается только выяснить, что в этом случае играет роль модуля Юнга Е.
При продольных волнах в среде возникают сжатия и разряжения отдельных слоев, и закон Гука в данном случае — связь избыточного давления р с относительным изменением длины элемента х цилиндрического канала / x — примет видp E / x, где знак минус связан с тем, что приращения давления р и длины противоположны по знаку. Умножив числитель и знаменатель на площадь поперечного сечения канала, получим
p – E V/V, |
(1.31) |
где V/V — относительное приращение объема рассматриваемого элемента. Перейдя к пределу, получим
E – V dp/dV. |
(1.32) |
Объем V элемента х и его плотность меняются при прохождении волны, но их произведение, т. е. масса V = const. Отсюда d / = –dV/V, значит
dV – V d / . |
(1.33) |
После подстановки этого выражения в (1.32) получим E = dp/d , и скорость волны — формула (1.26) — примет вид
v |
dp/d |
. |
(1.34) |
Это выражение справедливо для волн в жидкостях и газах. Опыт показывает, что при распространении звука в газе
связь между давлением и объемом определяется уравнением
pV const, |
(1.35) |
где — так называемая постоянная адиабаты, равная отношению теплоемкостей газа при постоянных давлении и объеме,Cp/CV — величина, характерная для каждого газа. Запишем дифференциал натурального логарифма выражения (1.35):
dp dV 0,
pV
