Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2798

.pdf

Скачиваний:

Добавлен:

13.02.2021

Размер:

24.88 Mб

Скачать

☆

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 2324 / 2724 25 26 27 > Следующая >>>

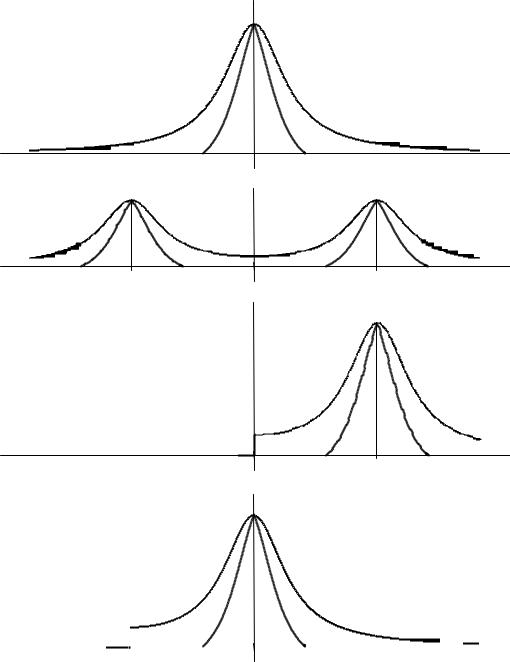
				230
		1
− j		2	A(ω − ωo ) , ω > 0
		2		(10.45)
υ(ω )=	1		*	(10.45)
	1		*
j	2	A		(ω + ωo ) , ω < 0
	2

A(ω)

а)

− ωmax 0	ωmax	ω
б)	S(ω )

− ωo	0	ωo	ω

( )

Z ω

в)

0	ωo	ω
	ωo

AГ (ω )

г)

− ωo

Рисунок10.8

– Спектральныеплотности:)комплогибающейксной

A(t );

б)физическогосигнала

s(t );в)аналитическогосигнала

Z (t);

г)комплекснойогибающейпоГильберту

AГ (t)

231

Переходякспектральнымплотностямкомплексныхогибающихфиз

ческого A(t ) исопряженного Aυ (t ) сигналов,получим

Aυ (ω)= − jA(ω).

Физическузкополрадипредйоссобойныйигналтавляетумму квадрасост(10урныхавляющих.4)

s(t )= Re[A(t )e jωot ]= Re{[Ac (t )+ jAs (t )] (cosωot + j sinωot )}= = Ac (t ) cosωot − As (t ) sinωot .

Сигнал,сопряженныйпоГильберту,

− такжеузкополосный.Онбудетиметь

(− j ).

комплексногибающую,отличамножщуюся

ениемна

As (t )− jAc (t ).

Aυ (t )= − j[A(t )]=

jωot

]= Re{[As (t )− jAc (t )] (cosωot + j sinωot )}=

υ(t )= Re[Aυ (t )e

Этотжерезультатможнополучитьдругимпутем.

= As (t ) cosωot + Ac (t ) sinωot .

jωot

] являетсяаналит

Если ωo > ωmax ,токомплефункциясная

[A(t )e

ческимсигналом,т..ееспекрасположентольковобластип ложительных

частот,.е.

jωot

= s(t )+ jυ(t ).

Z (t )= A(t )e

Представиманал сутическийгналдействительноймоймнимойчастей

Z (t )= [A

(t )+ jA (t )] [cosω

t + j sinω

t]=

= Ac (t )cosωot − As

(t )sinωot + j

Ac (t )sinωot + As (t )cosωot .

s(t )

υ(t )

Выпрасчетогибающейлняя,полн

ойфазыимгновеннойчастоты,получим:

A(t )=

s2 (t)+υ2 (t)

Ac2 (t)+ As2 (t)

;

Ψ(t )= arctg

υ(t )

= ωot + arctg

(t )

;

s(t )

(t )

Aʹ (t ) A

(t )− Aʹ (t ) A

(t )

ω(t )= Ψʹ(t )= ωo +

(t )+ A2 (t )

Пример10.2

Рассчитатьогибающую,полнуюфазумгновеннчастотидеальную

гополосигнала, овпектрогорого

ограниченинтерваломчастот

[ω1,ω2 ].

и-

(10.46)

(10.47)

и-

(10.48)

(10.49)

(10.50)

(10.51)

(10.52)

о-

232

S(ω)

а)

− ω2

− ω1

ω1

ω2

Z (ω)

2So

б)

ω1

ω2

Рисунок10.9

– Спектральноепредстфизического)(вл ние

ианалитическ огоб()сигналов

Спектральнойплотности

Z(ω),изобнарисункеаженной10б),соо.9

т-

ветствует аналситическийгнал

Z (t )

ω2

Z (t) =

∫

e jω t =

[(sinω

t − sinω t )

− j(cosω

t − cosω t )].

π t

ω1

и-

Физическаяогибающаяисходногополосигналасовоп одает

бающейаналитическогосигнала

So (ω2 − ω1)

sin

ω2 − ω1

A(t) =

(sinω

t − sinω t )2

+ (cosω

t − cosω t )2 =

π t

ω2 − ω1

Полнфазполосовогоасигналаяопределитсяф (10рмуле.51)

cosω2t − cosω1t

2 sin

ω2t +ω1t

sin

ω2t −ω1t

ω1 +ω2

Ψ(t)

= −arctg

= arctg

sinω

t − sinω t

2 cos

ω2t +ω1t

sin

ω2t −ω1t

Нако,мгнчаовенецсигтотравнналая

ω(t) =

Ψ(t) =

ω1 + ω2

=ωo .

Мгновеннаяч

астотанезависитотвремеравцентральнойияетсяч

а-

сттогоите

нтервала,вкотсосредоромспек.

точенр

			233
10Выводы.5
1Узкополосные. сигналызанимдиапазширинач ,ютсткоторого
значитцентральнойменьшечастоты.Узкополосныесигналыназываюткв					а-
зигарм,т.к.ихогибнчческимиамедленностотающаяменяютсявовр				емени.
2Узкопол. сигналыудобсные			нопредстчерезквавлядратурныеко ь		м-
поненты,аогибающуюфазу			– черезкомплексогибающую.Понятие
комплекснойогибаюобобпонятиещкомплексныхейаетамплитудгармон					и-
ческихколебан.Комплекснаяогиобъединяетйбающаявсемедленные“ ”пр					о-
цессыиявляет	сянизкочастотнымэквивалентузкополрадиосимного			гнала.
Естественнаяогибающаяузкополосногосигналаравнмодулю					м-
плекснойог	ибающейинезависитотзначенияцентральнойчастоты.
Обобщеннаяфаузкополосногосигналаравнсуммеаргумента					м-
плексной огибающейлинейногослагаемого,значениякоторогопрямо					о-
порцентральнойиональночастоте.
3Квадратурная. обрабузкосигналткаполосныхпозвнайтивляет
огибающуюфазовыйуголузкополосногопроцесса.
Определзаконаизмфазовогоенуглаиеенияспо				мощьюквадратурной
обрхарактеризуетботкилинарастающейейнопогрешностью, опояли					р-
наячастотапринесовпадаетмникацентральнойча тотойпектрасигн. ла
4Определение. огибфазыспомощьюющейаналитическогосигнала
независитотцентральнойча			стоты.Аналсиигналтическиймеетнимую
вещечасти,связатвенпаройпреобразованийныеуюГильберта.Физич					е-
скийузкополосныйсигналравенреальнойчаналитическогостисигнала.
Спектраналитическсигналалежитполнвобластиположительныхстьюго
частот.Спектркомплексно		−сопряженногоаналитическогосигналалежит
полнвобластиотрицастьючас. тельныхот
5Модуль. иаргументаналисигналаназываютическогоогибающей
обобщеннфаузойкоппроцессапойГильбертулосного.
ОгибающаяпоГильбертусовпадает			сфизическойогибающейвтом
случае,есликомплексогибающаясигхарактеризуналаограниченнымтся
спектром,приверхняячемаспектретаогибающейменьшецентральной
частотыузкополосногосигнала.
Мгновеннаячастотаузкополосногосигналаравнпрои				звоаднойт	р-
гументааналитическогосигнала.
6Преобразо. фильтр( )Гильберта,связывающийательмеждусобойф					и-
зическиузкополосныйисигнал,сопряженныйГильберту,пре					д-
ставляетсобойчастотно		−независимыйфазовращатель,которыйосуществляет
поворотфазывсехгармконическихлебанаодиуголийаковый				− π	.
Операции,связанныепреобразованиямиГильберта,становятсяфиз				2	и-
Операции,связанныепреобразованиямиГильберта,становятсяфиз					и-
ческиреализусущественноупрощаютсямыми,еслиузкополосныйсигнал
представленквадратуркомпо. нымиентами

234

11МЕТОДЫАНАЛИЗАПР

ОХОЖДЕНИЯУЗКОПОЛОСН

ЫХ

РАДИОСИГНАЛОВЧЕРЕЗ

ИЗБИРАТЕЛЬНЫЕЦЕПИ

11Понятие.1низкочастотногоэкв збирательнойвален

цепи

Припередачеинформациинарасстояниеширокпр пм лучилнение

способчастотногоразделениясигнало

в.Дляэтойцелипр узкопменяются

о-

лосныесигналы,которыезанимаютполосучастмнменьшенекоторойго

центральнойчастоты

ω0.Выделениенужногосигналаприемеосущест

в-

ляетсяпомощьючастотно

-избирательныхцепей,полосапропусканиякот

о-

рыхрасполаг аетсявокрестностирезонанснойчастоты

ωР.Примеромпр

о-

стейшполосовыхфиявляютсяльтровпоследовательныеипараллельные

конту.Анализпрохождеыу кополосныхсигналовчерезизбирательныея

цеписущественноупрощаетсяприиспользованиикомплексныхогиб

ающих

узкоппроцесс,анализулокотныхосвященарыхпредыд

ущаяглава.

Вкомплексформеможпредставитьнонетолькоузкополосныйси

г-

нал,ноиимпульснуюхарактеристикуизбирательнойцепи

( ) =

[ ( )

jωPt ],

(11.1)

g t

Re G t

где G(t) – комплекснаяогибающимпульснойхара;яктеристики

e jωPt - быосциллирующаятрофункциявремени;

ωP - резонанснаячастокон,близкаятурачасвтоколеббодныхте

а-

ний.

Комплекснуюогибающую

н-

G(t) называютнизкочастотнымэквивале

томи пульснойхарактерисизбирательнойцепи. ики

Поаналогииссигналомимпульснуюхарактеристикуцепиожно

и-

сатьполусуммойкомплексно

-сопряженныхфункций

jωPt

− jωPt

g(t)

G(t) e

(t) e

(11.2)

ПрименпрямогоеобразниеФурьек(11по.ваниязволпол2), ет

у-

читькомпередаточнуюлексфуизбирательнойкциюцепиввидесуммы

комплексно-сопряженныхсоставляющих,смещенныхокрестностьточек

± ωР.

235

(ω +ωP ),

где

Φ[g(t)]= K

(ω) = K(ω −ωP )+ K

K(ω −ωP ) =

G(ω −ωP ),

(ω +ωP )

(ω +ωP ).

Спектральнаяплотностькомплексной

огибающей

G(t)

внутриполосыпропусканиявокрестностирезонанснойчастотыбыстро

тухаетпомереудалотнее.Поэтомуниядлявысокодобротныхизбирател

ныхсистемвзаимнымвлияниемкомплексно

-сопряженнслагаемых

можнопренебречь

(ω −ωP ) =

G(ω −ωP ),ω < 0,

K (ω) =

(ω +ωP ) =

(ω +ωP ),ω >

НизкочастотэквивалентомНЧ( ым

- эквизбирательной) валентомц

пиназываютвоображацепь,комплексредаточнаямуюфукоткция

ройполучапутемсмоднощениятся

йиздвухкомплекскомпо, ныхент

например,

(ω −ωP ) изокрестностичастоты

ωР вокрестностьнуля.Дляп

реходакНЧ

- эквивалентудостатвыпозамену(11ч переменных.о4)ить

ω = ωP + Ω

ИмпульснаяхарактеристикаНЧ

KНЧ (Ω) =

G(Ω).

- эквиваленсточндопостаьюоя

ногомножителя

совпадаеткомплекснойогибающейимпульснойхара

теристикиизбирательнойцепи

gНЧ (t) = Φ−[KНЧ (Ω)]= 12 G(t).

11Расчет.2НЧ – эквивалентовпростейшихколебательных цепей

(11.3)

(11.4)

(11.5)

сосредоточена а- ь-

( )

К ω

(11.6)

е- о-

е-

(11.7)

н- к-

(11.8)

Простейшиепоследовательбательныепаралко ко туры изучаютвкурО« стенцепейовы»рии.

Частотныехарактерисизбирательныхцепейзавоткисят главного параметра,называемогообобщеннойрасстройкой.

236

		ω		ωP
	ξ = Q	ω	−	ωP	.
	ξ = Q		−		.
		ωP
		ωP		ω
Отточноймоделиобобщеннрасстройкилегкперейтиприближе
ной,т.к.впределахполосыпропусконтуратечастотанияущая
ческинеотличаетсярезонансной	ωР,т.е.			ω + ωР ≈ 2ω.

(11.9)

н- а ω практи-

ξ = Q

(ω − ωP )(ω + ωP )

≈ 2

(ω − ωP ).

(11.10)

ω ωP

ωP

Пример11.1

− РасчетНЧ

-эквивапослеколебательндовательногонта

о-

гоконтура.

L(t)

Комплпередаточныефукстрехкции

u(t)

возможныхвариа

нтповстроенияпослед

о-

R(t) вательнколебательногозапнтура

и-

шутсяввиде:

uC(t)

Рисунок11.1

KR (ω) =

ωP

R + j ωL −

+ jQ

−

ωC

ωP

jωL

jω L R

K L (ω ) =

R + j ωL −

+ jQ

−

ωC

ωP

jωC

ωCR

KC (ω) =

ωP

R + j ωL −

+ jQ

−

ωC

ωP

Перехотточноймоделиобобщеннойярасстройкиприближенной, получимсмещенну ювточку ωР составляющуюкаждизтрехмплексныхй передаточныхфункций.

237

KR (ω −ωP ) ≈

1 + j

(ω −ωP ) α + j(ω −ωP )

ωP

KL (ω −ωP ) ≈

= jQ

1 + j

(ω −ωP )

α + j(ω −ωP )

ωP

(ω −ωP ) ≈ −

= − jQ

1 + j

(ω −ωP )

α + j(ω −ωP )

ωP

где α = ωP

ωL

≈

ωP L

= Q ,

≈

= Q .

ωCR

ωPCR

Выползаменупереяя

менных ω = ωP + Ω,найдемНЧ

– эквиваленты

трце.ПользуясьхпейобратнымпреобФурье, ассчитазованием

м-

пульсныехарактеристики.

−α t

НЧ

(Ω )

НЧ

(t) = α e

t ≥ 0 .

α + jΩ

−α t

НЧ

(Ω )

= jQ

НЧ

(t)

= jQα e

t ≥ 0 .

α + jΩ

−α t

НЧ

(Ω )

= − jQ

gС

НЧ

(t) = − jQα e

, t ≥ 0 .

α + jΩ

ВсетриНЧ

– эквивалентасто

чностьюдопостоянногомножителясо

в-

падаютспростейшимфильтромнижнихчастотпервогопорядка.Нарисунке

11изображечастот.2 характнытрмоделейристиких

KС (ω),

(Ω) (Расчетвыполнендля

Q=5специально,чтобыпоказать

KС (ω −ωP ),

KСНЧ

поведениечастотхарактерис, меняяыхмасштаба). ик

238

K(ω)

(ω )

(ω − ω p )

а)

− ω

(ω + ω p )=

(ω + ω p )

K (ω −ω p )=

G(ω −ω p )

б)

− ω

ωсв ≈ω p

K НЧ (Ω)

в)

ω =ω p + Ω

− Ω

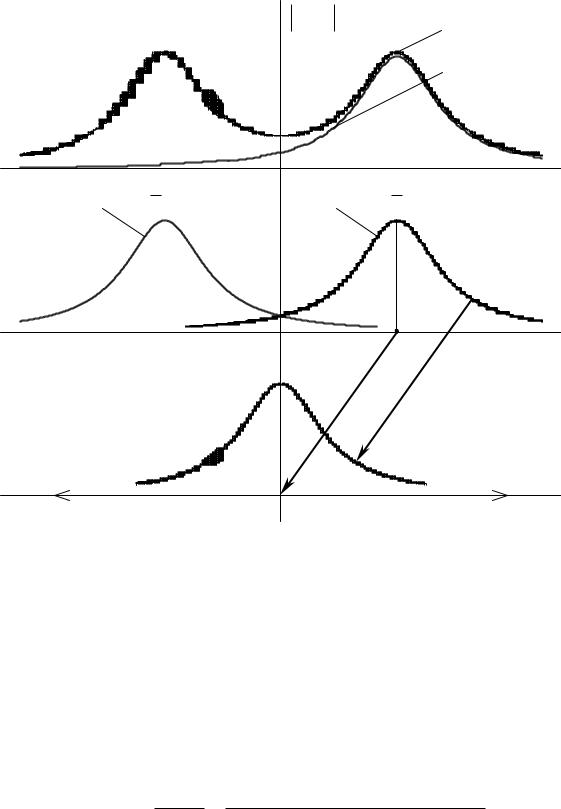
Рисунок11.2

– Частотныехарактерисизбирательныхцепей: ики

а) амплитудно-частотнаяхарактеристика;б)представкомпперлекснойние

е-

даточнойфункци

исуммойдвухкомплексно

-сопряженныхсоставля

ющих;

в)низкочастотныйэквивализбирательнойц пинт

11Расчет.3НЧ

– эквивалентапроизвольнойчастотно

избирательнойцепи

Коэффициентпередачиполосовогофильтопефразапторнойрме

и-

сипредст авляетсобойдробно

-рациональнуюфункциювида

K (p) =

H1(p)

(p − p

)(p − p

H1(p)

)(p − p

(11.11)

(p)

)(p − p

)...

где p1, p3

–

комплекполюса,располвоныевтчетвертиоройженные

р –

плоскости;

239

p2, p4 – комплексно-сопряженныеполюса,расположвтретьче енныей

т-

верти р – плоскости.

Представим K(p) суммойпростыхдробей

(11.12)

K (p) = ∑ An

(pn )

n=1

− pn

где N – количествополюсов,соста мплексноляющих

-сопряженныепары.

H1(p)

(p − p

) =

)

(11.13)

H2 (p)

p= pn

Разложениепереда

точнойфункциинапростыедробипозволяетра

K− (p),однаизкоторых

с-

формировать K(p) надвеподгруппы

K+(p) и

K+(p)

объединяетнечетныеполюса,другая

– четныекомплексно(

-сопряженные

полюса).

K (p) = K+ (p)+ K−(p).

Индексы(+)и -)соответствуютположительнымотрицачас. ельнымотам

N 2

(p) = ∑ A

)

p − p2n −1

n =1

2n −1

−1

N 2

(p) = ∑ A

)

p − p2n

−

n =1 2n

Отбрасывая K− (p),п ереходимктакназываемойукороченнойфун

N 2

(p) = ∑ A

)

− p2n −1

n =1

2n −1

Заменяя

на

jω

иподставзначениялюсовяя

p2n −1 = −α2n −1 + jω2n −1,получаемматематическописаниечастотнойх е

рактеристики,смещеннойвокрестностьцентралчастотыной

ωЦ

(11.14)

(11.15)

(11.16)

кции

а-

N 2

(ω −ω

)= ∑ A

(−α

+ jω

)

jω + −(−α2n −1 + jω2n −1 )

(11.17)

НЧ

n =1

2n −1

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 2324 / 2724 25 26 27 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023126.95 Кб02750.pdf
#
05.02.2023249.87 Кб02753.pdf
#
05.02.2023466.68 Кб0279.pdf
#
13.02.20212.11 Mб12790.pdf
#
13.02.20211.28 Mб222797.pdf
#
13.02.202124.88 Mб32798.pdf
#
05.02.2023441.35 Кб2280.pdf
#
05.02.2023145.68 Кб02825.pdf
#
05.02.2023436.03 Кб02837.pdf
#
05.02.2023214.23 Кб02838.pdf
#
05.02.2023294.91 Кб02839.pdf