
2798
.pdf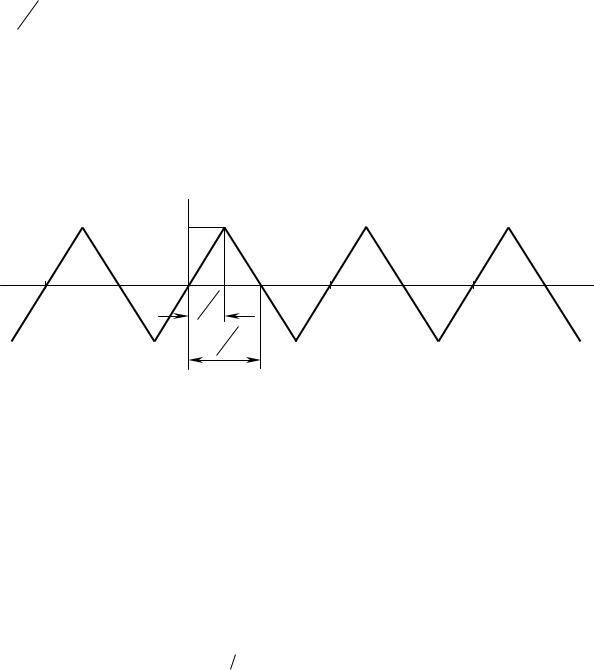
|
60 |
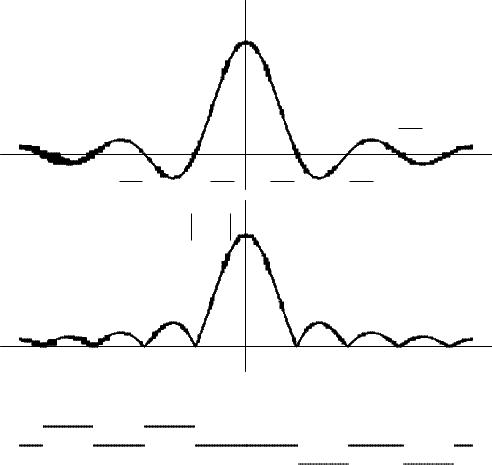
Анализспектров,представленныхтаблице2показывает.6,чтоог |
иба- |
ющиекомплекспектрн сятдинныхжеопульсирующийтвхарактер, |
|
таккакниформаимпу,ниихдлитьсовнменяютсяльность. |
|
Сувеличинтмеждуимпульсаплитудырваланиемгармонич |
е- |
скихолебауменьшаются.Частотыийгармк ническихлебауменьший |
а- |
ются.Ширспектрасигннаостаетсянеизменлов,дляееоценкиможноой |
|
2π |
|
|||
использовполовинушириныгллепесткавноготьспектра: |
ω ≈ |
при |
||||
|
||||||
τ ≤ T |
|
|
|
τ |
||
.Срос |
томперипроперераспреисходитдаэнергиимеждуеление |
|
|
|
||
2 |
|
|
|
|
|
|
постояннойипеременнойсоставляющимисигнала |
: энергияпостоянной |
|||||
составляющейпада,энпеременнойргиясоставляющейрастетпри |
|
|
|
|||
неизменнойполосе. |
|
|
|
|
||
2.Пример9.гармонического5 анализапериодической последоватзнакочередующихсяимпульльно тиов треугольнойформы
|
E |
|
− T |
T |
T |
|
4 |
|
|
T 2 |
|
Рисунок2.15 |
– Периосигналдвумяическийвидасимметрии |
|
Анализируявремпредставнноесигнала,изобениераженного |
и- |
сунке2видим.15,чтозадансигявлныйал |
яетсянечетнойфункцивремени, й |
поэтому |
|
∞
s(t )= ∑bn sin nω1t .
n=1
Крто,сигналгомебладаетзеркальнойсимметрией,..повторяется черезполовперспринуодативопзнаком,следовательносмложным(.та б- лицу2.3)
0, |
|
n = 2,4,6... |
|
|
|
T 4 |
|
|
8 |
||
bn = |
∫ |
s(t ) sin nω1tdt, n = 1,3,5... |
|
|
|
||
|
|||
T |
|
||
|
|
0 |
|

61
Выполнимматема |
тичеописакоеиг,изобналаиенарисуаженного |
|
н- |
||
ке2.15. |
|
4E |
|
|
|
|
s(t )= |
t, 0 < t ≤ T |
4 |
. |
|
|
|
||||
|
|
T |
|
||
Рассчитываемвескоэффициентвой |
|
bn |
|
|
|
bn
=
|
|
|
|
|
T 4 |
|
|
|
|
|
|
|
|
|
|
T 4 |
|
|
|
|||||
|
|
|
8 |
|
|
|
4E |
|
|
|
|
32E |
|
T 4 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= |
|
|
|
|
∫ |
|
|
t sin nω1tdt = |
|
|
UV |
|
0 |
− |
∫ |
VdU |
= |
|||||||
T |
|
T |
T 2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
32E |
|
|
1 |
|
|
T 4 |
1 |
T 4 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
+ |
|
|
|
|
|
|
|
= |
|
|||||||||||
|
|
|
|
|
|
t |
− |
|
cos nω1t |
|
|
|
∫cos nω1tdt |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T 2 |
nω1 |
|
|
0 |
|
|
nω1 |
0 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
32E |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
T |
|
|
|
|
sin nω T |
|
|
|
||||||||||
= |
|
|
|
|
− |
|
t cos nω |
+ |
|
|
|
|
. |
|
|
|||||||||
|
|
|
|
nω |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
T |
2 |
|
1 |
4 |
|
|
2 |
|
|
|
1 |
|
4 |
|
|
|||||
|
|
|
|
|
|
1 |
|
|
|
|
(nω ) |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
Подставляя |
nω1T |
|
= n |
π |
,получ имдлянечетных |
n |
||||||
4 |
|
|
2 |
|||||||||
|
|
|
|
|
|
1, |
|
n = 1,5,9... |
||||
cosn |
π |
|
= 0 |
, |
sin n |
π |
|
|||||
|
= |
|
|
|
||||||||
|
|
2 |
1, |
n = 3,7,11... |
||||||||
|
2 |
|
|
|
|
|
− |
|||||
2m −1 = n |
,где |
m |
|
1,2,3... |
|
|
|
|
|
|
|||||||||
Пусть ( |
) |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
π |
1)m+1. |
||||||||
|
|
|
|
|
|
|
|
sin n |
|
|
= (− |
||||||||
|
|
|
|
|
|
|
|
2 |
|||||||||||
|
b |
|
= |
|
8E |
sin n |
π |
= |
8E |
|
(−1)m+1 |
. |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
n |
|
|
(nπ )2 |
|
|
|
|
2 π 2 (2m − 1)2 |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
8E |
∞ |
|
|
|
|
m+1 |
|||||||||
|
s(t )= |
∑ |
(− 1) |
|
sin(2m − 1)ω1t . |
||||||||||||||
|
2 |
(2m − 1) |
2 |
||||||||||||||||
|
|
|
π |
|
m=1 |
|
|
|
|
|
|||||||||
2Выводы.10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Бескповтонечноворяющеменийся |
|
|
|
|
|
|
|
|
|
|
|
|
физическийпроцессможет |
||||||
бытьпредставленпериодичессигналспользуемым,ш окимор |
|
|
|
|
|
|
|
|
|
|
|
|
|
е- |
|||||
шениипрактическихзадач. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Подгармоническиманализомпонимаютразложениепериодического |
|
|
|
|
|
||||||||||||||
сигналасуммугармоникчастотами,кратосновнчастоымиповтйе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о- |
|
рения перипоследовательностидической. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3. Суммиргармсопределеннымивниканиемплитудаминачал |
|
|
|
|
|
|
|
|
|
|
ь- |
||||||||
нымифазамипозволяетвосстанпериодическийсигнлюбойвитьзада |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
н- |
||
нойточностью. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

62
4. |
Подспектральнымихарактеристикамипериодическогосигнала |
|
|
|
о- |
||
нимаютраспределени |
еамплитуд(начальныхфаз)почастотаминазывают |
|
|
|
|||
спектрамиамплитудфазсоответственно. |
|
|
|
|
|
||
5. |
Времиспектральноенноепредставленияоднозначноописывают |
|
|
|
|
||
периосигнвдическийвухраплоскостяхзных:мгновензначеноеи |
|
|
|
– вре- |
|||
мяиамплитуда |
– частотаначал( |
ьнаяфаза |
– частота). |
|
|
|
|
6. |
Времпредставленноепериодическогосиг,какправилоналаие, |
|
|
|
|
|
|
аналоговаяфункцияврем.Спектральнпредставлениепериодического |
|
|
|
|
|
||
сигнала – дискретнзатухающаяфункцияч .стоты |
|
|
|
|
|
||
7. |
Экспериментальноеисследоизменениясигналаввр |
|
s(t) |
|
емени |
||
осуществляетсяпомощьюосциллографа,поэтому |
|
называютосцилл |
о- |
||||
граммой.Экспериментальноеисследованиеспектральногососигнтавала |
|
|
|
|
|
||
выполняетсяпомощьюанализат |
|
оспектраиназываетсяспектрограммой. |
|
|
|
||
8. |
Формапериодического |
игналазависитнетолькоотспектраампл |
|
|
и- |
||
тудно,изначенийтначальныхфазгармоник.Еслиначальныефазыгарм |
|
|
|
|
о- |
||
никлибо0 |
π,топериодическийсигналобладаетчетнсимметриейотнос |
|
|
|
и- |
||
тельноначалако.Еслирдинначальныефгармоникзыт |
|
|
± π |
,топериод |
и- |
||
ческийсигналобладаетнечетнойсимметротносначалакоордиейтельно |
|
|
2 |
|
и- |
||
|
|
|
|
||||
нат.Еспектрамплитудзатухамедленно,топериодическийтсигналим |
|
|
|
|
е- |
||
етразрывы.Еспектрелиамплитудисчезают“ ”некоторыегармоникиили( |
|
|
|
|
|
||
огибспектраамплитудющ я |
|
пульсирует),этопримпульсногознакх |
|
|
а- |
||
рактерапери |
одическогосигнала. |
|
|
|
|
|
|
9. |
Мощностьпериодическогосигналасложнойформыравнасумме( |
|
|
|
|
|
|
общемслучаебесконечной)мощностейотдельныхгарм ническихста |
|
|
|
|
вля- |
||
ющих.Погрешноаппрокпериодическогосигналтьимации |
|
|
аконечнойсу |
м- |
|||
мойгарморавразностимощностаиксигналаконсуммыегачной |
|
|
|
|
рмо- |
||
ник. |
|
|
|
|
|
|
|

63
3ГАРМОНИЧЕСКИЙАНАЛ ИЗНЕПЕРИОДИЧЕСКИХ СИГНАЛОВ
3Предельный.1 переходотпериодическихсигналов кнепери одическим
Изложенныйвглавегармоническ2 анализпериодсигналовческихй можнораспростнанепесигналранитьодические ы,есливвыражении(2.3) периодустркб сконечностимить
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim s(t )= lim |
∑sT (t + kT )= sT (t ). |
|
|
|
|
(3.1) |
|||||||||||||||
|
T →∞ |
T →∞ k =−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Рассмотризменения,провспектресходящиепериодическогоси |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г- |
|||||||
нала s(t ) приувеличениипериода,напримереперипоследователдической |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ь- |
|||||||
ностиимпу |
льсов,представленнойтаблице2При.6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T →∞ коэффициенты |
||||||
|
|
|
|
|
|
|
|
|
|
|
An = 2 |
|
Cn |
|
уменьшаютсядобе |
с- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Cn ,а,следовательно,иамплитудыгармоник |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
конечномалойвеличины,кртого,расстояниеме |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω междучастотами |
о- |
||||||
седнихгармоник |
nω1 и (n + 1)ω1 стремятсякнулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Кажущеесяисчезновение“ ” |
|
|
|
|
|
информациипроисходитиз |
|
|
|
|
|
|
|
|
-занарушения |
|||||||
энергетичпериодическогохсоотношен.Эн рг иягналай |
|
|
|
|
|
|
|
|
sT (t ) конечна. |
s(t ) беско- |
||||||||||||
нечна,аэнергиянепериодическогосогнала |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Чтобыисключвозникающееэнергетическоетьпроти,совморечие |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е- |
|||||
стимгармоническийанализвосстановлениесигналапоспектрусинтез( ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ВоспкомплекснымльзуерядоФурьев(таблицеся2. |
|
|
|
|
|
|
|
|
|
T / 2 |
|
|
|
|
|
|
|
|
1) |
|
||
|
∞ |
|
jnω1t |
|
|
|
1 |
|
|
|
|
|
− jnω1t |
|
|
|||||||
|
|
|
|
|
∫s(t ) e |
|
|
|||||||||||||||
|
s(t )= ∑Cne |
|
|
|
|
,где |
Cn = |
T |
|
|
|
dt. |
|
|||||||||
|
n=−∞ |
|
|
|
|
|
|
|
|
|
−T / 2 |
|
|
|
|
|
|
|
|
|
||
Подставим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cn ввыражениедлякомплрядаксного |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
∞ |
|
|
1 |
|
T 2 |
|
− jnω t |
|
|
|
|
|
jnω t |
|
|
||||||
|
s(t )= ∑ |
|
|
|
∫sT (t ) e |
dt |
|
e |
|
|
||||||||||||
|
|
|
|
|
|
|
1 |
|
|
1 . |
|
|
||||||||||
|
|
T |
|
|
|
|
|
|
|
|||||||||||||
|
n=−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
−T 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Устремляяпериодкбесконечнпереходяпределу, стилучим |
|
|
|
|
|
Cn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∞ 1 lim s(t )= lim ∑
T →∞ T →∞ n=−∞ T
T / 2
∫sT (t )e− jnω1t dt
−T / 2
e jnω1t . (3.2)
64
При T →∞ расстояниемеждуспектральнымилиниями |
|
|
|
|
|
|
|
|
|
ω уменьша- |
||||||||||||||||
етсядобесконечномалойвеличины |
|
|
|
|
|
|
|
1 |
|
|
dω ,т.е. |
|
dω |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
lim |
|
= lim |
|
|
ω |
= |
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Часотдельныхотыгармк ничлебабудутменскихяий |
T →∞ T |
|
T →∞ |
|
2π |
|
2π |
|
тьсянеди |
|
с- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
кретно: |
ω1, |
2ω1, 3ω1, … nω1,анепре,обтекущуюразывночастотуя |
|
|
ω ,т.е. |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
lim nω1 = ω . |
|
|
|
|
||||||||||
Дискретнаяумма(3преобразуется.2)винт |
|
|
|
T →∞ |
|
|
|
|
|
|
|
|
егральнсуммбескую |
|
о- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
нечнымипредпот кущелпарамиметру |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω .Врезультатеполуча тся |
|
|
|||||
двойнойинтегФурьеал |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
∞ |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
s (t ) |
= |
|
∫ |
|
∫ |
s |
|
(t ) e− jω t dt e jω t dω . |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
T |
|
|
2π |
|
|
T |
|
|
|
|
|
|
|
|
|
(3.3) |
||||||||
|
|
|
|
|
|
|
−∞ −∞ |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
S |
(ω )= lim (CnT ) |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T →∞ |
|
|
|
|
|
|
|
|
|
|
|
|
ВнутреннийинтегралназываетсяпрямымпреобразованиемФурье |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
(ППФ)Формаль. ППФобозначао |
|
|
|
|
|
|
|
|
|
|
|
ется |
Ф+[s(t )].Результатомприменения |
|
|
|||||||||||
ППФксигналу |
s(t ) |
являспетсяктральнаяплотность |
|
|
|
|
|
|
|
|
|
S(ω) .Спектральная |
||||||||||||||
плотность S(ω) − эток мплефунчастотык,котцияснаяможнопрерую |
|
|
|
|
|
|
|
|
|
|
|
д- |
||||||||||||||
ставить какэ вивалентныйвкладсехпектральныхсоставляющих,наход |
dω . |
|
|
|
|
|
|
|
|
|
я- |
|||||||||||||||
щихсявнутричастоинтерваланого |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|||||
|
|
( ) |
= |
|
|
|
( |
|
|
) |
= |
lim |
|
= |
2πCn |
. |
(3.4) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
S ω |
|
|
lim TCn |
|
|
|
|
ω |
Cn |
dω |
||||||||||||||
|
|
|
|
T →∞ |
|
|
|
|
|
|
T →∞ |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|||||
Внешнийинтегралв(3называется.3)обратнымпреобразованиемФурье |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(ОПФ)Формаль. ОПФобозначаетсяо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф−[S(ω)].Результатомприменения |
s(t ) |
|
|||||||||
ОПФкспектральнойплотностифункц( частоты)являетсяигнал |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
||||
функциявремени. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3Прямоеи.2 обратноепреобразованияФурье |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Существуютдваспописсобанепернияс .гналаодического |
|
|
|
|
|
|
|
|
|
|
|
|
Первый |
|||||||||||||
способнматематическомованпредставлфизичсигналаскогонии |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
функцивремений |
|
s(t ).Второйспособ |
|
|
|
– |
описанфизичсигналаеского |
|
|
|||||||||||||||||
функциейчастоты |
S(ω) .Этидвапредставмеждуиясигналасвязаны |
|
|
|
|
|
|
|
|
|
о- |
|||||||||||||||
бойпре |
образованиямиФурье: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
65
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
( )= |
Ф |
+[ ( )]= |
( ) − jω t |
dt |
, |
|
(3.5) |
||||||||||||
|
|
S ω |
|
|
|
s t |
∫s t e |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
( )= |
Ф |
−[ |
( )] |
= |
1 |
∞ ( ) |
jω t |
dω |
. |
(3.6) |
|||||||||
|
|
|
|||||||||||||||||||
|
|
s t |
|
S |
ω |
|
2π |
∫S |
ω e |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t .Произведение |
||
|
Размерностьчастоты |
|
|
|
ω образмерноститнавремени |
|
|
|
|
|
|
||||||||||
параметров ω и t |
– безразмервеличинаая |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
ωt = 2πft . |
|
|
|
|
|
|
|
|
(3.7) |
||||
|
Функции s(t ) и S(ω) описываютразличнойф рмединтотжеф |
|
|
|
|
|
|
|
|
и- |
|||||||||||
зическийпроцесс.Функция |
|
|
|
|
s(t ) даетпредставлениеосостояниисистемы |
|
|
S(ω) позволяетоп |
|
||||||||||||
координатахмгновен“ значеноеи |
|
|
|
|
|
|
|
|
– время”Функция. |
|
|
|
|
и- |
|||||||
сатьп оведениесистемыкоординаампли“ тахуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– частота”. |
|
||||
|
Интересопоинснотформулегральнкомплексногоавитькоэффы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и- |
|||||
циентарядаФурье |
|
испек |
траплотностиьной |
|
|
|
|
|
|
|
|
||||||||||
Cn |
|
|
|
|
S(ω) : |
|
|||||||||||||||
|
|
|
|
|
|
|
1 |
|
T / 2 |
|
− jnω1t |
|
|
|
|
|
|
|
|||
|
|
|
|
Cn |
= |
T |
∫sT (t )e |
|
|
dt |
, |
|
|
||||||||
|
|
|
|
|
|
|
−T / 2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S(ω) = ∫sT (t )e− jω t dt . |
|
|
|
|
||||||||||||
|
Спектральнаяплотность |
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
с- |
||
|
|
|
|
|
|
– непрерывнаяфункциячастоты.Комплек |
|
|
|
||||||||||||
ныйкоэффициент |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с- |
|
Cn – дискретнаяфункциячастоты.Размерностькомплек |
|
|
|
|
|
|
|
||||||||||||||
ногокоэ |
|
|
рядаФурьесовпадаразмерностьюисследуемого |
|
|
|
|
|
|
|
|||||||||||
ффициента Cn |
|
|
|
|
|
|
|
||||||||||||||
сигнала s(t )
[s(t )]= [Cn ].
Размерносспектральнойплотностиравнапроизведеразмерниюости сигнала s(t ) и времени
[S(ω)]= [s(t )] [время].
Значспенияктральнойплотнодискретных,взятыеочках |
|
|
T совпадаютзначениями |
ω = nω1,сточндопостмножителяьюоянного |
|
|
|
|
|
|
|
коэффициентов Cn |
|
|
|
|
|
(nω1). |
(3.8) |
T Cn = S |
|||
СравниммеждусобойкомплексныйрядФурьеиобратноепреобраз |
|
|
о- |
ваниеФурье: |
|
|
|
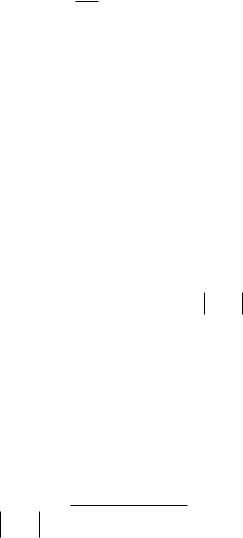
66
∞
s(t )= ∑Cne jnω1t ,
n=−∞
1 sT (t )= 2π
РядФупредставляетьепериодическуюфункцию
бесконечногочислагармоник, кретныезначения
∞
∫S(ω)e jω t dω .
−∞
s(t ) суммойхотяи
функцию sT (t) интегральнсуммойбесконечномалыхпамплитудейга |
|
|
моникс |
епрерывнойпоследовательностью |
частот. |
3Спект.3 характеристикинеперльныесигналоводических |
|
|
Спектхарактеристикилиспектральной( плотностью)непй |
оты S(ω) . |
|
риодсиназываютгналаческогокомплефунчасткснуюцию |
||
∞
S(ω)= ∫s(t ) e− jω t dt = A(ω)− jB(ω)= S(ω)e jϕ(ω ),
−∞
∞
A(ω)= ∫s(t )cosωtdt = Re S(ω),
−∞
∞
− B(ω)= − ∫s(t )sinωtdt = ImS(ω).
−∞
Модульиаргументспектральнойпл тностипределяютсявыражени
S(ω ) = 
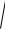 A2 (ω )+ B2 (ω ),
A2 (ω )+ B2 (ω ),
|
ϕ(ω)= −arctg |
B(ω) |
. |
|
|
||
|
|
A(ω) |
|
Модулькомплекснойспектральной |
|
плотностиназываютампли удно |
|
частотнойхарактерАЧХ()спектрасигнстикойла |
|
|
s(t ).ЧастоАЧХили |
с-
р-
е-
(3.9)
(3.10)
(3.11)
ями: (3.12)
(3.13)
-
|
S(ω) |
|
называютамплиспектром.Аргууднымко спектралплекснойент |
|
|
|
|
|
|
ь- |
||
|
|
|
|
|
|
|
|
|||||
нойплотностиназываетсяфазочастотнойхарактеристикойФЧХ()сп |
|
|
|
|
|
|
ектра |
|||||
сигнала s(t ).Втехнлитературечской |
|
|
ϕ(ω ) называютфазовымспектром. |
|
||||||||
АЧХ – четнаяфункциячастоты,ФЧХ |
|
|
– нечетнаяфункциячастоты,.. |
|
||||||||
|
|
|
|
( ) |
|
= |
|
( |
) |
|
, |
(3.14) |
|
|
|
|
|
|
|
||||||
|
|
|
|
S ω |
|
|
S −ω |
|
|
|
||
|
|
|
ϕ(ω )= −ϕ(− ω ). |
(3.15) |
||||||||
|
|
|
|
|
|
|
|
|
|
67 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Пример3.1 |
- Расчетспектхараодиночногольныхктепристикям |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о- |
||||||||||||||||||||||
угольногоимпульса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Одиночномупрямоугоимп,длительнулькоторсуномугость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S(ω) . |
τ,а м- |
|||||||||||||||||||
плитуда E (рисунок3соотв.1),спектральнаятствуетплотность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
s(t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S(ω ) |
|
|
Eτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− τ |
0 |
τ |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4π |
|
|
0 |
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
4π |
|
|
|
|
ω |
||||||||||||||||||||||||||||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|
|
|
|
|
|
|
|
|
|
τ |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
а) |
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок3.1 |
− Временноеа)(испектб() едставальноесигналаения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
τ / 2 |
− jω t |
|
|
|
2E e jωτ 2 |
− e− jωτ 2 |
|
|
|
|
|
|
|
sinωτ 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
∫Ee |
dt |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= Eτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
S(ω)= |
|
ω |
|
|
|
|
2 j |
|
|
|
ωτ |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
−τ / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
При ω = 0 спектральнаяплотностьчислерав ноа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щадисигнала |
|
|
|
||||||||||||||||||||||||||||
∞
S(0)= ∫s(t )dt = Eτ .
−∞
Сигналописываетчетнойфункциврем,спяениктральнаяплой ность − действительнойфункциейчастоты
нечнойэнергиейконечнойдлительностью носзатсувеличениемухаетьчастоты,затуханиеноситпульсирующий“ ” характПереход. спектральнойплотностичерезднознсвязачно длительностьюимпульса тральнойплотностим жноценчастотлосуватьсигнала.
Дляпостроенияспектхарарисунок(льныхктеристик3необходимо.2) рассчитатьмодульиаргументспектральнойплотности:
|
|
|
sinωτ |
|
|
|
S(ω ) = A(ω ) = Eτ |
|
|
2 |
|
|
, ϕ(ω) = |
|
|
|||||
|
|
|
|
|
ωτ 2
S(ω)= A(ω).Сигналобладаетк |
т- |
о- |
|
τ ,поэтом успектральнаяпло |
т- |
|
к- |
0 |
, A(ω) > 0 |
} при ω > 0, |
− π , A(ω) < 0 |
||
arg S(ω) = |
, A(ω) > 0 |
}, при ω < 0. |
0 |
||
+ π , A(ω) < 0 |
|
|
68
S(ω )
Eτ
а) |
|
|
|
6π |
|
|
|
|
|
||
− 4π |
− 2π |
2π |
4π |
τ |
|
ω |
|||||
− ω |
|
|
|
||
τ |
τ |
τ |
τ |
|
S(ω)
б)
|
|
|
|
− ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
||
|
|
в) |
|
|
|
|
|
|
ϕ(ω ) |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− ω |
|
|
|
|
|
|
|
|
|
|
|
− π |
|
|
|
|
|
ω |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Рисунок3.2 |
− Спектральные характеристикипрямоугоимпу: льсаного |
S(ω) = A(ω); |
|||||||||||||||||||||||
а)спектральнаяплотность |
|
|
|
|
− действительнаяфункциячастоты |
|
|
|
|||||||||||||||||
б) |
|
S(ω) |
|
амплспектриамплитуднотудный |
|
|
|
|
|
|
|
|
−частотнаяхарактеристика |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
(АЧХ)спектрасигн;в) ла |
|
|
|
|
ϕ(ω ) − фазовыйспектрилифазочастотнаяхара |
|
|
к- |
|||||||||||||||||
териФЧХ()спетисигнктрала |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
3Анализ.4внутреннструктунеперсигналайыодического |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Любпроизвольныйсигнал |
|
|
s(t ) можетбытьпредставленсуммойче |
|
|
т- |
|||||||||||||||||
ной sчет (t ) инечетно й sнеч (t ) составляющих: |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
s(t )= sчет (t )+ sнеч (t ), |
|
|
|
(3.16) |
|||||||||||
|
|
|
|
s |
(t )= |
1 |
[s(t )+ s(− t )], |
s |
неч |
(t )= |
1 |
[s(t )− s(− t )]. |
(3.17) |
||||||||||||
|
|
|
|
|
чет |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||
Здесь s(t ) − исходсиг, налый |
|
s(− t ) − сигналввеор.емсиейни |
|
|
|
||||||||||||||||||||
Определим спектральныеплотчетнойтии ечетнойоставляющих
сигналаобщеговида:
Ф+ [s(t )]= Ф+ [sчет (t )]+ Ф+ [sнеч (t )],
|
|
|
|
|
|
|
|
69 |
|
|
|
|
|
|
Ф+[s |
|
∞ |
|
|
|
|
∞ |
|
|
∞ |
|
|
||
(t )]= |
∫ |
s |
(t )cosωtdt − j |
∫ |
s |
(t )sinωtdt = 2 |
∫ |
s |
(t )cosωtdt , |
|||||
чет |
|
чет |
|
|
|
чет |
|
чет |
||||||
|
|
−∞ |
|
|
|
−∞ |
|
|
0 |
|
|
|||
|
|
|
+[ |
|
|
|
∞ |
|
|
|
|
|
|
|
|
Ф |
( )] |
( ) |
|
|
|
( ) |
, |
|
|
(3.18) |
|||
|
|
sчет t |
= A ω |
= 2∫sчет t cosωtdt |
|
|
|
|||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
∞ |
|
|
|
∞ |
|
|
|
∞ |
|
|||
Ф+[sнеч (t )]= ∫sнеч (t )cosωtdt − j ∫sнеч (t )sinωtdt = −2 j ∫sнеч (t )cosωtdt ,
−∞ |
−∞ |
0 |
|
|
∞ |
Ф+[sнеч (t )]= − jB(ω)= − j2∫sнеч (t )sinωtdt .
Любсигналуобщегомувидасоответс |
|
|
|
|
|
|
|
0 |
||
|
|
|
|
|
|
|
|
твуетспектральнаяплотность |
||
S(ω)= A(ω)− jB(ω),причем |
|
A(ω) – спектральнаяплотностьчетнойсоста |
||||||||
ляющей, |
− jB(ω ) – спектральнаяплотннечетнойост. авляющей |
|
||||||||
|
s(t )= s |
|
|
(t ) |
+ s |
неч |
(t ), |
|
S(ω)= A(ω)− jB(ω). |
|
|
чет |
|
|
|
|
|
|
|||
|
|
+ |
[s |
|
|
|
|
(ω) |
= A(ω) |
|
|
Ф |
|
|
(t )]= Re S |
||||||
|
|
|
|
чет |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
Ф |
|
[sнеч (t )]= j ImS(ω)= − jB(ω) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
(3.19)
в-
(3.20)
Есигналли |
s(t ) представлясобойчетнуюфункциювремени,то |
|
|
|
|
|
|
s(t ) |
|||||||||||||||
спектральнаяплотность |
– действительнаяфункциячастоты.Е игналли |
|
|
|
|
|
|
||||||||||||||||
представляетсобойнечетфункциювремеую |
|
|
|
|
|
|
|
|
|
|
ни,тоспектральнаяплотность |
|
– |
||||||||||
чистомнимфункцияча.стоты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A(ω) и B(ω) позволяет |
|||||||
ПрименобратпреобразованияФурьеогоиек |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
определитьотдч льнонечетнуюс ставляющиесигналаобщеговида: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
s |
|
(t )= |
1 |
|
∞ A(ω) e jω t dω = |
|
|
||||||||||
|
|
|
|
|
|
|
|
2π |
|
|
|||||||||||||
|
|
|
|
|
|
чет |
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
∞ |
−∞ |
|
|
|
|
∞ |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
||||||||
= |
|
|
∫ A(ω)cosωtdt + j |
|
∫ A(ω)sinωtdt = |
|
∫ A(ω)cosωtdt |
, |
|
||||||||||||||
|
2π |
|
2π |
|
|
|
|
(3.21) |
|||||||||||||||
|
|
|
−∞ |
|
|
|
|
|
−∞ |
|
π |
0 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
sнеч (t )= |
|
1 |
|
∞[− jB(ω)] e jω t dω = |
|
|
|||||||||||
|
|
|
|
|
|
2π |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
∞ |
|
|
|
1 |
|
∞ |
|
1 |
|
∞ |
|
|
|||||||
= |
|
|
∫ B(ω)sinωtdt − j |
|
|
∫B(ω)cosωtdt = |
|
∫ B(ω)sinωtdt . |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
(3.22) |
|||||||||||||
|
2π |
−∞ |
|
|
|
2π −∞ |
|
π |
0 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0
