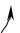2798
.pdf
|
|
191 |
|
|
|
временноеиспектральноепредставленияАМ |
|
|
−сигналапритонмодльной |
|
у- |
ляции. |
|
|
|
|
|
sy (t) |
|
|
B |
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
t |
|
Ω |
|
ω |
so (t) |
Ao |
|
|
Ao |
|
|
|
|
|
|
|
|
t |
|
|
ωo |
ω |
sам (t) |
|
|
|
|
|
Ao |
|
{An } |
Ao M |
A |
Ao M |
Amax |
Amin |
o |
|||
2 |
|
2 |
|||
|
t |
|
|
||
|
|
ωo − Ω ωo ωo + Ω ω |
|||
|
|
|
|
2Ω |
|
|
|
{ϕn } |
|
ϕo |
ϕo +ϕy |
|
|
ϕo −ϕy |
|
||
|
|
|
|
|
|
|
|
t1 t2 t3 t4 |
t5 |
t |
|
|
ωo − Ω ωo ωo + Ω ω |
|
|
|
а) |
|
|
|
|
б) |
|
Рисунок8.3 |
− Временноеа)(испектб() едставленияальто оеаль |
|
|
ной |
||||
|
|
|
амплитудноймодуляции |
|
|
|
||
Анализируявремпредставлениенное,отмечаемоднозначнуюсвязь |
sy (t) иогибающейАМ |
|
|
|||||
междууправляющимсигналом |
|
−сигнала.Ес уб |
и- |
|||||
намодуляции |
M = 0 (или |
sy (t) = 0),тоАМ |
−сигнал превнесущееращается |
|
||||
колебание.Если |
M =1,тонаступает100 |
% модуляция,прикоторой |
|
|||||
Amax = 2 Ao , |
Amin = 0 . |
|
|
|
|
|
|
|
Обспектральноеуждаяпредставление,обращвнимачетемиеую |
|
|
|
|
|
|||
симмспамплитудектратриюотносите |
|
|
льнонесущегоколебан.Амплитудыя |
|
||||
боколебанийвыхравнымеждусобой.Максизнамплитудычениеальное |
|
|
|
|
|
|||



|
|
|
|
|
|
|
|
|
|
|
|
|
|
196 |
|
|
|
|
|
|
|
|
|
|
|
|
S |
ам |
(ω )= Ф[s |
ам |
(t )]= Ф[A cos(ω |
o |
t + ϕ |
o |
)]+ Ф[k |
ам |
s |
y |
(t )cos(ω |
o |
t + ϕ |
o |
)]= |
||||||||||
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= π A e− jϕo δ (ω + ω |
o |
)+ π A e jϕo δ |
(ω − ω |
o |
)+ |
|
|
|
|
|
|
|
(8.22) |
|||||||||||||
|
1 |
o |
|
|
|
|
1 |
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
+ |
kам e |
− jϕo |
|
|
|
kам e |
jϕo |
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
S y (ω + ωo )+ |
2 |
|
|
S y (ω − ωo ). |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Нарисунке8изображвременное.7 сп ктральноепредста |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вления |
||||||
сигналовприамплитмоднеперуляцднойсигналом.одическим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S y (ω ) |
|
|
|
|
|
||
|
|
|
sy (t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ao cos(ωot + ϕo ) |
|
|
|
πAoδ (ω + ωo ) |
|
|
|
|
πAoδ (ω − ωo ) |
||||||||||||||
|
|
|
|
|
|
t |
|
|
|
− ωo |
|
|
|
|
|
|
Sам (ω) |
|
ωo |
|
|
|
||||
|
|
|
|
|
|
|
|
|
kам |
|
|
|
|
|
|
|
kам |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
S y (ω + ωo ) |
|
|
|
|
2 |
S y (ω −ωo ) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
sам (t ) |
πAoδ (ω + ωo ) |
|
|
|
|
|
|
πAoδ (ω − ωo ) |
|
|
|
||||||||||||
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Рисунок8.7 |
|
– Времиспектральноенноепредставлениянепериодического |
|
|
|
|
|
|
|
|
ϕo = 0) |
||||||||||||||
|
|
управляющего,н |
есущегоимодулированногосигналовпри( |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
8Балансная.5 иоднополоснаямодуля |
|
|
|
|
|
|
|
|
|
|
|
|
ция |
|
|
|
|
|
||||||
|
|
КромеобычнойАМ,применяеамплимодстподавленусяляциядная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и- |
||||||
емнес |
ущей – баланснаямодуляцияБМ(). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Балансно−модулированноеколебаниеБМ( |
|
|
|
|
|
|
|
-колеб)можнозапкакисатье |
|
|
|
|
||||||||||||
|
|
sбм (t) = kбм s y (t) so (t) = kбм |
s y (t) Ao cos(ωot + ϕo ) = |
|
|
(8.23) |
||||||||||||||||||||
|
|
= Aбм (t) cos(ωot + ϕo ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Здесь Aбм(t) = kбм Ao sy (t)−огибающаямодулиров |
|
|
|
|
анногоколебания(8.23); |
|
||||||||||||||||||||
kбм − коэффициентпропорциональности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
197 |
|
|
|
|
|
|
|
|
Еслиуправляющийсигнал |
|
sy (t) |
инесущееколебание |
so (t) однораз- |
||||||||
мерныевеличины,напримернапряженияили(токи), |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
[kбм ]= |
|
или |
|
|
|
|
|
|||
|
|
B |
|
А |
. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
Пусть |
sy (t) = B cos(Ωt +ϕ y ). Полагая ϕ0 |
= ϕy |
= −π / 2,представимБМ |
|
- |
|||||||
колебаниеввиде |
|
sбм (t) = kбм A0 B cos(Ωt −π / 2) cos(ω0t −π / 2) = |
|
|
||||||||
|
|
(8.24) |
||||||||||
|
|
= Aбм cos(ω0 |
− Ω)t + Aбм cos[(ω0 |
+ Ω)t −π ], |
|
|||||||
|
|
|
|
|
||||||||
где Aбм = kбм А0 В - амплитудабоксоставляющейвой. |
|
|
|
|
|
|
|
|
||||
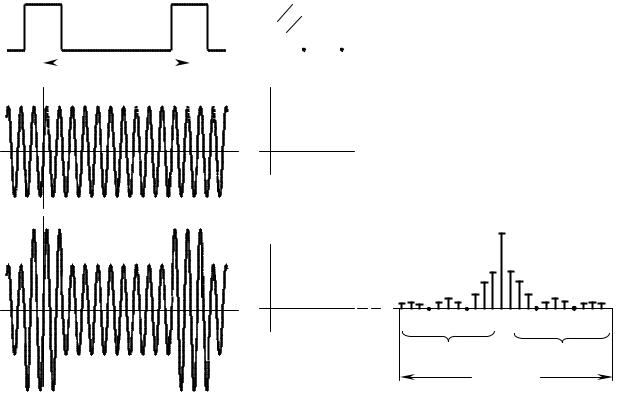
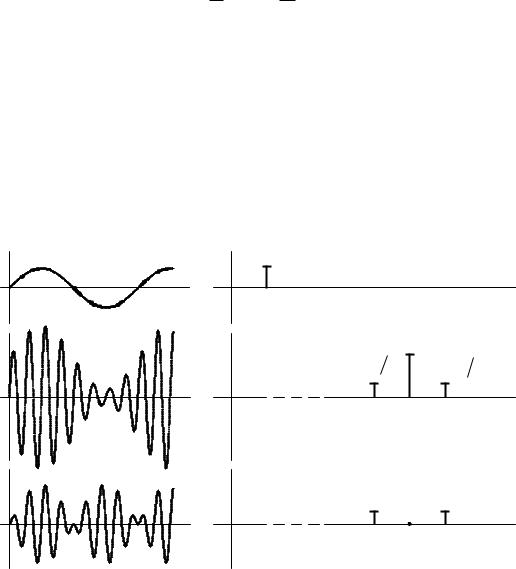
Длясравнениянарисункеизоб8.8временныеажены |
|
|
|
|
|
|
|
диаграммы |
|
|||
спектральсоставдвухсигналовый |
|
|
sам (t) и sбм (t) примодуляциигармон |
|
и- |
|||||||
ческимуправляющимсигналом |
sу (t). |
|
|
|
|
|
|
|
|
|||
sy (t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
Ω |
|
|
|
|
ω |
|
sам (t) |
|
|
{An } |
|
|
|
|
A0 |
A M 2 |
|
|
|
|
|
|
|
|
|
|
|
|
A0 M 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
t |
|
|
|
|
|
|
ωo − Ω ωo ωo + Ω ω |
|
||
sбм (t) |
|
|
{An } |
|
|
|
|
AδM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
ωo − Ω ωo ωo + Ω ω |
|
||
|
|
а) |
|
|
|
|
|
|
б) |
|
|
|
Рисунок8.8 |
– Временноеа)(испектб() едставленияальноерадиосигнала |
|
|
|
|
|
|
|
||||
|
|
привыпол ненииАМБМ |
|
|
|
|
|
|
||||
Главнымдостоинствомпростойамплитмодявулятодной, етсяции |
|
|
|
|
|
|
sy (t) (информати в- |
|||||
чтоф рмагибающейточноповторязаконизмененият |
|
|
|
|
|
|
|
|||||
ныйсигнал)Поэтому. ддетектятакогосидостаточноргналаванияприм |
|
|
|
|
|
|
|
|
|
е- |
||
нитьоднополупериод |
диодныйдетектор. |
-колебания Sбм (ω) ,такжекакиАМ |
|
|
|
|||||||
СпектральнуюплотностьБМ |
|
|
|
|
- |
|||||||
колебанияпримодуляциипроизвольнымнеперсигналомодическим |
|
|
|
|
|
|
|
|
sy (t), |
|||

198
можновыразитьчерспектральнуюплотностьгибающей.Полагая,что |
|
|
|
|
|
|
|
|
|
|
|
|
|
S y (ω) ,получим |
|
|
||||||||
сигналу sy (t) соотвспектральнаятствуетплотность |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
S |
|
(ω) = |
1 |
k |
бм |
A [S |
y |
(ω −ω |
o |
) + S |
y |
(ω + ω |
o |
)]. |
|
(8.25) |
|||||||
|
2 |
|||||||||||||||||||||||
|
бм |
|
|
|
|
o |
|
|
|
|
|
|
|
|
|
я- |
||||||||
Такимобраз,спектрмодулирующегомсигналаврезультатемодул |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
циираздваивается“ ”,..смещпоосич насяот |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
± ωo .Ширинаспектра |
|
|
||||
БМ-колебанияувеличиваетсяраза2посравнениюширинойспектра |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
управляющегосигнала. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
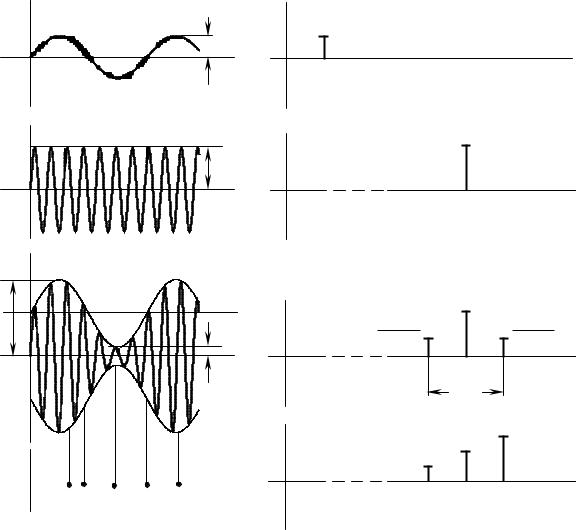
Прибаланснмодуляциинарушаетсяоднозначнаяй связьмеждуупра |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в- |
||||||||
ляющимсигналомогиб.Вч ющейстностипри(гармоническомуправл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
я- |
||||||||
ющемсигнале),выхБМодезнб"и"вениярезультатекаютсложения |
|
|
|
|
|
|
|
|
|
|
|
|
(ω0 ± Ω).Периодби" |
|
|
|||||||||
двухгармконичеслебанийблизчастотамиких |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е- |
|||||
ний"вдварменьшезапериодауправляющегосигнала. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ПриБМувеличиваетсяотносительнаядолямощности, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
связаннаяп |
е- |
||||||||
редачейинфдо50%рмацииЭтосвязанотем.,чтоБМп зволяетсократить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
расходмощностинапередачуколебнесущейчастотыния.Еслимодулир |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у- |
|||||
ющийсигнал |
sy (t) содержитпостсоставляющуюянную,тоспектреБМ |
|
|
|
|
|
|
|
- |
|||||||||||||||
колебаниявозн |
икаетомпонентанесущейчастоты. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Дальнейшееснижениеэнергосвяприменениемзаоднополоснойтрат |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
амплитмод, осуществленляляцииднойкотпоройдавляют,помн имо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е- |
|||||
сущегоколе,однуизбанияокповспелосвых |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ктреБМ |
|
−сигналарисунок( 8.9). |
|
|
|||||
|
|
|
sy (t) |
|
|
|
|
|
|
|
sбм (t ) |
|
|
|
|
|
|
|
|
s0 м (t ) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ПФ |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
A0 cosωo t |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
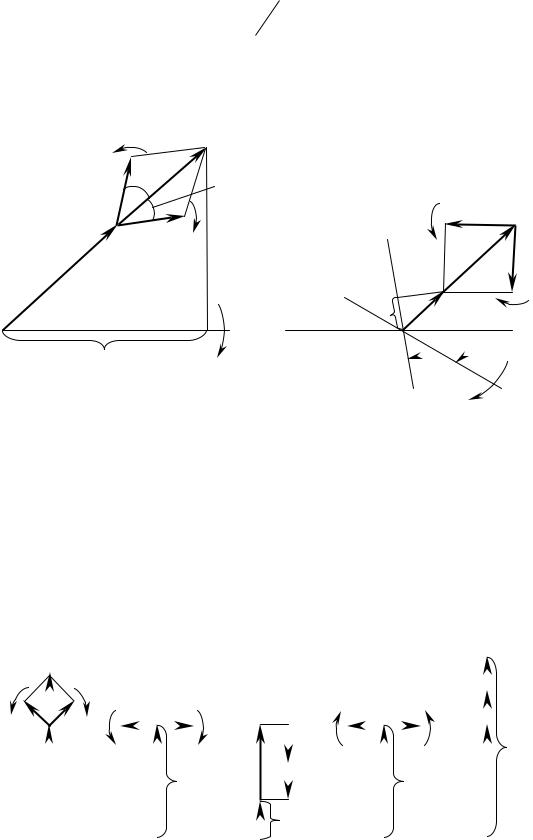
Рисунок 8.9 – Реализациябалансноднополм йдуляцииспомощьюсной |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
перемножителяполосовогофильтраПФ() |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Длявосстановлениямодулирующегосигналадостаточсохранитьв |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
спектремодулировсигналлишьоднубокапнного:либолосувуювер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х- |
|||
нюю,либонижнюю.Для |
|
|
|
|
передачибокотребуетсялосвыхтолькопол вина |
|
|
|
|
|
|
|
|
|||||||||||
полосычастот( |
|
ω вместо 2 |
|
ω)Так. сппередачиойсоб,называемыйодн |
|
|
|
|
|
о- |
||||||||||||||
полоснамплитойдОМ(у)сподавлениемляциейднойнесущей,позволяет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
максимасократитьпольно |
|
|
|
|
|
|
суча |
стот,занимаемуюсигналом. |
|
|
|
|
|
|
||||||||||
ПриприемеОМ |
|
|
-колебанийнеобходимовосстаколебаниеавливать |
|
|
|
|
|
|
|
е- |
|||||||||||||
сущейчастоты( |
|
Ao cosωot )инижнююбокпочастотлосувуюНБП(),что |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
усложняетприемник.Затрудненияустсразвитиемняютсяэлементнойбазы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(схемы восстаннесущегок лебания,влсхвосстаномы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вленияНБП). |
|
|
|||||||


 ϕ
ϕ