Однако если выбрать 0 = −1, то метод быстро сойдется. Чтобы облегчить выбор начального приближения, сформулируем следующую теорему.

Теорема 45.1 (Достаточное условие сходимости метода Ньютона). Если ( ) · ( ) < 0, причем ′( ) и ′′( ) отличны от 0 и сохраняют определенные знаки при 6 6 , то исходя из начального приближения 0, удовлетворяющего неравенству ( 0) · ′′( 0) > 0, можно вычислить единственный корень уравнения ( ) = 0 с любой степенью точности.

Заметим, что данное условие не является необходимым. Однако в данном случае мы не сможем выбрать такие и , чтобы условие выполнялось при 0 = 0. Заметим, что если выбрать = −5, = −1, 0 = −1, то условие выполняется и метод действительно сходится.

Таким образом, не стоит применять его бездумно. Но при должном анализе метод Ньютона сослужит хорошую службу.

4Метод золотого сечения

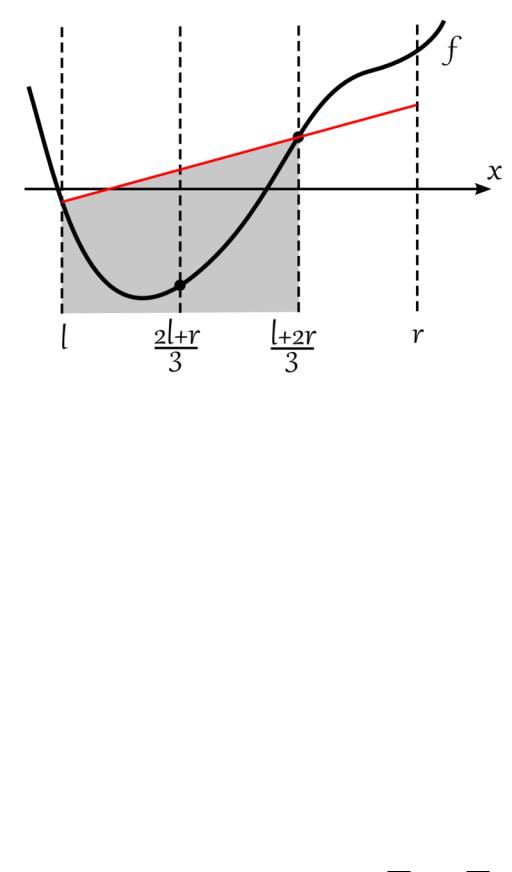
Сейчас мы рассмотрим метод (а также его небольшую модификацию), который позволяет искать минимум (максимум) некоторой непрерывной унимодальной функции. Функция ( ) называется унимодальной на отрезке [ , ], если , 6 6 : [ , ) ( ) ( ( ) ) и ( , ] ( ) ( ( ) ). Иными словами, функция унимодальна, если [ , ], такое, что при < функция не убывает (не возрастает), а при > функция не возрастает (не убывает). Несмотря на то, что унимодальные функции встречаются не так часто, а исследование на унимодальность зачастую нетривиально, этот метод может быть полезен. Например, если мы можем разбить исходную область поиска функции X на отрезки, на которых они унимодальна, то для нахождения глобального минимума достаточно выбрать минимум из найденных значений на каждом отрезке.

Для начала рассмотрим более простой тернарный поиск. Будем считать, что функция( ): [ , ] →R непрерывна на отрезке [ , ] и унимодальна на нем, причем ! : [ , ], ̸=( ) > ( ) (насчет строгости данного неравенства будет сказано ниже). Как и раньше, мы хотим найти минимум с некоторой точностью . Метод очень похож на метод бисекции: мы также сужаем границы поиска до тех пор, пока не найдем с нужной погрешностью искомую точку.

1.Если выполняется − < , то искомый минимум найден (в качестве его можно взять,

например, точку ′ = +2 ). Посчитаем значения функции в точках = 2 3+ и = +23 . Теперь рассмотрим несколько вариантов:

( ) > ( ). Это возможно в двух случаях. Если < и > , то искомый минимум лежит где-то на отрезке [ , ] (а точнее на [ , ]). Если же < и < , то минимум лежит на отрезке [ , ] (а точнее на [ , ]). Поскольку мы можем не знать точно, какой из случаев имеет место, то выберем такие новые границы для отрезка [ ′, ′], чтобы по-прежнему в любом случае выполнялось ′ 6 6 ′. В качестве такого нового отрезка подходит [ , ]. Иными словами, необходимо поставить = .

( ) < ( ). Этот случай абсолютно симметричен предыдущему. Если < и> , то искомый минимум лежит на отрезке [ , ]. Это продемонстрировано на рисунке ниже. В случае > и > минимум также лежит на отрезке [ , ]. Значит, необходимо поставить = .

149

( ) = ( ). Вот тут стоит быть внимательным. Если мы точно знаем, что функция строго унимодальна, т.е. она сначала строго убывает, а потом строго возрастает, то данное равенство возможно лишь в случае < и > , а значит, в качестве новых границ поиска следует задать = , = . Заметим, что ради упрощения этот случай можно отнести к любому из вышеперечисленных, поскольку какие бы новые границы мы не взяли, отрезок [ , ] будет принадлежать любой из них. Однако если мы не можем гарантировать строгую унимодальность, то тернарный поиск неприменим. Действительно, в таком случае возможно еще 2 варианта: < , < и> , > . И тут уже нельзя совершенно точно сказать, какие новые границы поиска следует задать. Если взять их за [ , ], то в случае > , > искомый минимум выйдет за пределы отрезка. Если же принять [ , ], то это же самое произойдет при < , < .

2.После установки новых границ поиска вернемся к шагу 1.

Оценим скорость работы данного метода. После каждой итерации рассматриваемый отрезок уменьшается в 1.5 раза. Поэтому необходимое количество шагов для достижения нужной

точности можно оценить как = log3 ( − ) . Несмотря на то, что тернарный поиск работает

2

медленнее, чем метод бисекции, решаемая им задача сложнее. Внимательный читатель может заметить, что эту задачу можно решить, найдя производную функции, а затем ее 0 с помощью метода бисекции. Но такой вариант решения не подходит, т.к. мы не можем быть уверены, что ′( ) и ′( ) вообще существуют. Второй недостаток тернарного поиска заключается в том, что на каждом шаге необходимо вычислять значение функции в двух точках, что не очень эффективно. Поэтому оптимизируем данный поиск.

Заметим, что сходимость метода не зависит от выбора и на каждом шаге. Достаточно лишь выполнения условия < . Мы выбираем и как = 2 3+ и = +23 лишь для того, чтобы каждый раз делить отрезок [ , ] на 3 равные части, чтобы получать в некотором плане сбалансированное разбиение. Но, как мы сейчас выясним, это не самое оптимальное решение.

Попробуем подобрать такое разбиение отрезка на три части, чтобы на следующей итерации поиска одна из точек нового разбиения совпала с одной из точек текущего разбиения. Тогда

150

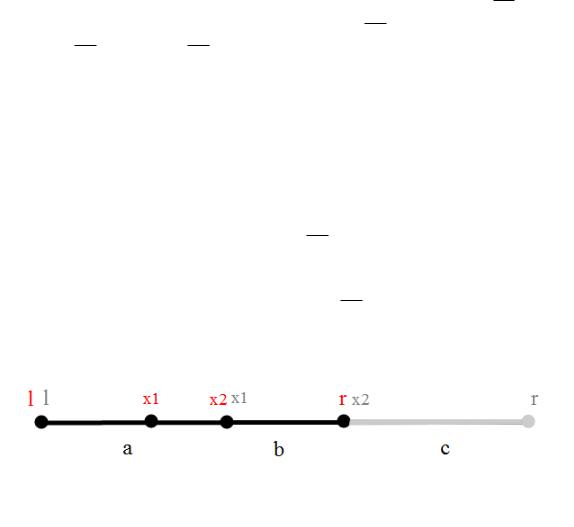
в следующий раз не придется считать функцию в двух точках, так как в одной она уже была посчитана. Пусть и — точки, которые мы хотим выбрать, — расстояние от до , ′ — расстояние от до , а ′′ — расстояние от до . Потребуем, чтобы выполнялось

Это не что иное, как золотое сечение. Теперь научимся вычислять точки и , пользуясь найденным отношением. Заметим, что достаточно найти и ′, тогда = + , = + + ′.

Как мы уже знаем, ′ + ′′ = . С другой стороны, ′ + ′′ = − − . Т.е. = +1− . Для суммы получаем следующее: + ′ = − − ′′ = − − = − − +1− .

Значит, = + +1− и = − +1− . Таким образом, метод золотого сечения выглядит следующим образом:

1.Вычисляем и , пользуясь указанными выше формулами, а также 1 = ( ) и 2 = ( ).

2.Если − < , то искомый минимум найден. Теперь рассмотрим несколько вариантов, как

ив тернарном поиске.

Если 1 > 2, то, как мы уже знаем, в качестве новых границ поиска следует поставить [ , ], поэтому сдвинем границу = . После такого сужения отрезка точка

должна перейти в точку , а значит следует поставить = и 1 = 2. Осталось лишь пересчитать значения для : = − +1− , 2 = ( ).

1 < 2, симметричный предыдущему случай. Новыми границами станут [ , ], т.е.

примем = . После этого сужения перейдет в , значит поставим = , 2 = 1. И вычислим новые значения для : = + +1− , 1 = ( ). Этот случай продемонстрирован на рисунке ниже. В наших обозначениях, 1 это , 2 это , а , , соответственно расстояния , ′, ′′.

1 = 2. Аналогично троичному поиску, мы можем рассматривать этот случай в одном из двух вышеперечисленных, если функция строго унимодальна.

3.Вернемся к шагу 2.

Таким образом, вычислить значение функции в двух точках нужно лишь на самой первой итерации, на каждой следующей мы пользуемся уже ранее посчитанными значениями. На каждом шаге область поиска сужается в ≈ 1.62 > 1.5 раз, т.е данный метод и сходится быстрее, нежели тернарный поиск.

151

5Градиентный спуск

Атеперь изучим метод поиска локального минимума функции многих переменных. Пусть есть точка 0, в окрестности которой мы хотим найти локальный минимум, и функция (¯). Рассмотрим последовательность точек:

1 = 0 − 0 ( 0),2 = 1 − 1 ( 1),

. . .

+1 = − ( ).

Здесь 0, 1, . . . , — некоторые вещественные числа, о выборе которых речь пойдет ниже. Вспомним, что такое градиент . Условно говоря, это направление наибыстрейшего роста функции. Аналогично можно заключить, что − — это направление наибыстрейшего уменьшения функции. Таким образом, мы можем ожидать, что ( 0) > ( 1) > . . . > ( +1), т.е. данная последовательность сходится к искомому локальному минимуму. В качестве критерия остановки метода можно взять (как и обычно) неравенство | ( ) − ( +1)| < .

Теперь обсудим самое главное, а именно выбор на -ом шаге. От этого во многом зависит сходимость метода. Существует 3 способа это делать:

0 = 1 = · · · = = , где = . Заметим, что в этом случае должно быть достаточно малым, чтобы метод не «скакал» вокруг искомого минимума. При неудачном выборе метод может никогда не сойтись. Однако для постоянного шага существует критерий остановки спуска:

Теорема 45.2. Пусть (¯) дифференцируема и ограничена снизу, а для градиента выполняется условие:

R : ′, ′′ E( ) | ( ′) − ( ′′)| 6 | ′ − ′′|.

Тогда , : 0 < < 2 ( +1) < ( ), причем lim ( ) = 0.

→∞

Иными словами, если выполняется условие теоремы, то метод сойдется при соответствующем выборе либо к локальному минимуму, либо (если минимума в окрестности нет)

к inf (¯).

+1 = , т.е. используется дробление шага. Мы не будем подробно анализировать данный способ, т.к. его анализ достаточно сложен. Следует отметить, что этот способ обладает обычно большей скоростью сходимости нежели предыдущий.

[0,+∞)

( ) − ( ) минимальна. Иными словами, мы выбираем так, чтобы следующая итерация была точкой минимума функции на направлении − ( ). Это проиллюстрировано на приведенном ниже рисунке. Заметим, кстати, что в этом методе направления соседних шагов ортогональны.

152