Часть 23

Исследование функций методами дифференциального исчисления I

1Условия монотонности функций

Между характером монотонности дифференцируемой на ( , ) функции ( ) и знаком ее производной существует следующая взаимосвязь:

1.′( ) > 0 ( ) ↑. Однако ( ) ↑ ′( ) > 0.

2.′( ) > 0 ( ) ′( ) > 0.

3.′( ) = 0 ( ) = ′( ) = 0 (критерий постоянства).

4.′( ) 6 0 ( ) ′( ) 6 0.

5.′( ) < 0 ( ) ↓. Однако ( ) ↓ ′( ) 6 0.

Все утверждения, что из левой части следует правая, были доказаны ранее. Докажем, например, утверждение из пункта 1. Остальные доказываются аналогично.

Утверждение 23.1. ( ) ↑ ′( ) > 0.

2Условия точек экстремума

Теорема 23.2 (необходимое условие локального экстремума). Если ( ) C( 0) и ( )

дифференцируема в некоторой U′( 0), причем ( ) имеет локальный экстремум в точке 0, то либо @ ′( 0), либо ′( 0) = 0.

Заметим, что данное утверждение является следствием из теоремы Ферма.

Теорема 23.3 (достаточное условие локального экстремума). Пусть ( ) C( 0) и ( )

дифференцируема в некоторой U′( 0). Тогда если ′( ) меняет свой знак при переходе через точку 0, то данная функция имеет в точке 0 локальный экстремум. При этом если ′( ) > 0 при U′( 0 −0) и ′( ) < 0 при U′( 0 + 0), то 0 — локальный максимум, в противном случае — локальный минимум.

Доказательство. Докажем часть утверждения, говорящую о локальном максимуме. Вторая часть доказывается аналогично. По теореме Лагранжа ( ) − ( 0) = ′( )( − 0). При

U′( 0 −0), ′( ) > 0, а − 0 < 0, т.е. ( )− ( 0) < 0. При U′( 0 +0), ′( ) < 0, а − 0 > 0, т.е. ( ) − ( 0) < 0. Значит, 0 — локальный максимум. [:|||||:]

Обратное неверно! Например, рассмотрим функцию, имеющую экстремум в точке, около которой производная функции не имеет определенного знака:

65

Здесь (0) = 0 и ( ) > 0 при ̸= 0, т.е. = 0 — локальный минимум. Теперь возьмем производную:

Можно показать, что ′( ) не имеет определенного знака ни в какой окрестности точки 0.

Теорема 23.4 (достаточное условие локального экстремума в терминах производной высших порядков). Пусть ′( 0) = 0 = ′′( 0) = (3)( 0) = . . . = ( −1)( 0), а ( )( 0) ̸= 0. Тогда при = 2 , ( ) имеет локальный экстремум в точке 0 (минимум при ( )( 0) > 0 и максимум при ( )( 0) < 0). Если же = 2 + 1, то 0 — точка монотонности ( ( ) ↑, если( )( 0) > 0, и ( ) ↓, если ( )( 0) < 0).

Доказательство. Напишем разложение ( ) в ряд Тейлора с остаточным членом в форме

3Асимптота графика функции

из ее односторонних пределов в 0, то прямая = 0 называется вертикальной асимптотой графика ( ).

= 0 — вертикальная асимптота.

66

Часть 24

Исследование функций методами дифференциального исчисления II

1Выпуклость функции и точки перегиба

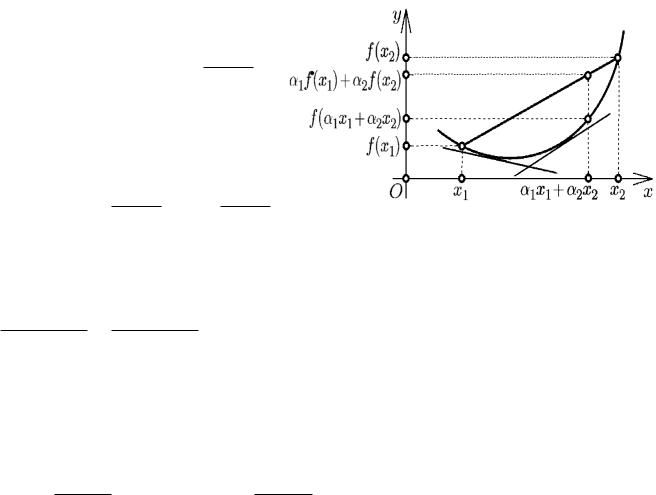
Будем называть ( ) выпуклой вверх на интервале ( , ), если 1, 2 ( , ) и 1, 2 > 0 : 1 + 2 = 1 ( 1 1 + 2 2) > 1 ( 1) + 2 ( 2). Соответственно, функция выпукла вниз, если в указанном неравенстве поставить 6. В случаях, когда неравенство строгое, говорят о строгой выпуклости функции.

Преобразуем указанное неравенство следующим образом. Для начала решим следующую систему:

Тем самым, мы доказали следующую теорему:

Теорема 24.1 (критерий выпуклости). Пусть ( ) дважды дифференцируема на ( , ). Тогда ( ) выпукла вниз т.и.т.т., когда ′( ) на ( , ). Причем строгое возрастание влечет строгую выпуклость.

Следствие 24.2. Пусть ( ) дважды дифференцируема на ( , ). Тогда ( ) выпукла вниз т.и.т.т., когда ′′( ) > 0 на ( , ). Если же ′′( ) > 0, то ( ) строго выпукла вниз.

67

2Геометрическая интерпретация выпуклости

Для начала вспомним, что кас = ( 0) + ′( 0)( − 0) — уравнение касательной в точке 0.

Теорема 24.3. Если ( ) дифференцируема на ( , ), то для ее выпуклости вниз необходимо и достаточно, чтобы все точки ее графика лежали не ниже любой касательной в любой точке интервала ( , ). Если ( ) строго выпукла вниз, то все точки графика (за исключением точки касания) лежат строго выше любой касательной.

Доказательство.

Необходимость.

Пусть ( ) выпукла вниз. Рассмотрим разность ( ) − кас = ( ) − ( 0) − ′( 0)( − 0). По теореме Лагранжа, ( ) − ( 0) = ′( )( − 0), где лежит между и 0. Тогда

получаем ′( )( − 0) − ′( 0)( − 0) = ( ′( ) − ′( 0))( − 0). Теперь если > 0, то и > 0, а, ввиду выпуклости вниз, ′( ) − ′( 0) > 0. Если же < 0, то и < 0, а значит, ′( ) − ′( 0) < 0. В любом случае, знак ′( ) − ′( 0) совпадает со знаком − 0,

а значит, произведение неотрицательно, т.е. ( ) − кас > 0, что и требовалось доказать.

Достаточность.

Снова рассмотрим ( ) − кас = ( ) − ( 0) − ′( 0)( − 0) > 0. Тогда получаем, что

{

А это не что иное, как определение выпуклости.

[:|||||:]

Следует отметить, что не стоит использовать геометрическую интерпретацию в качестве определения выпуклости. Например, функция ( ) = | | выпукла вниз по определению, но у нее не существует касательной в точке 0 = 0 (соответственно, использовать вышеприведенный критерий в качестве определения проблематично).

3Точки перегиба

Пусть ( ) дифференцируема на некоторой U( 0). Тогда если в окрестностях U−( 0) и U+( 0) различные направления выпуклости, то точка 0 называется точкой перегиба. Будем также требовать дифференцируемость функции в точке 0.

Например, ( ) = 3 имеет точку перегиба 0 = 0.

Теорема 24.4 (необходимое условие точки перегиба). Пусть функция ( ) имеет точку перегиба в 0, а ′′( ) непрерывна на некоторой U( 0). Тогда ′′( 0) = 0.

Доказательство. Предположим, что ′′( 0) > 0. Тогда U( 0) : U( 0) ′′( ) > 0.

Теорема 24.5 (достаточное условие точки перегиба). Пусть ( ) дифференцируема на

U( 0) и дважды дифференцируема на U′( 0). Тогда если @ ′′( 0) или ′′( 0) = 0, и ′′( ) меняет свой знак при переходе через 0, то 0 — точка перегиба функции ( ).

68