Московский государственный институт электроники и математики
(Технический университет)
Кафедра «Технологические системы электроники»
Применение среды MATLAB для моделирования на ЭВМ задач математической физики..
Курсовой проект
по курсу «Методы математической физики»
Выполнила студентка:
Князева М. П.
Группа Э-51
Преподаватель:
Якункин
М. М.
Москва 2011 г.
Задание:
Моделирование осциллирующей составляющей квазистационарного температурного поля при периодическом импульсном нагреве.
Краткое теоретическое введение:
Уравнение теплопроводности.
Уравнение
теплопроводности является дифференциальным
законом сохранения тепловой энергии
:
;
,
(1.1)
в котором
связь между температурой
и
тепловым потоком
задаётся в виде:
(1.2)
Подставляя
в (1.1) выражения для тепловой энергии
и
теплового потока (1.2), получим классическое
уравнение теплопроводности
;
, (1.3)
которое
является дифференциальным уравнением
в частных производных параболического
типа с постоянными коэффициентами.
Здесь
– теплоёмкость,
– плотность,
– коэффициент теплопроводности (
),
– коэффициент температуропроводности
(
).
Имея в
виду происхождение уравнения непрерывности,
иногда говорят, что функция
задаёт
температурное поле в образце. Различают
стационарные температурные поля, когда
тепловой поток
постоянен в любой точке образца
,
(
)
нестационарные, у которых температура
меняется во времени
и пространстве
,
и квазистационарные,
когда на фоне стационарной составляющей
возникают
пульсации температуры
,
так что
. (1.4)
Т.е.
возникает
- осциллирующая
составляющая решения
.
B
состоянии термодинамического равновесия
тепловой поток
равен нулю, а температура
постоянны во всем объёме образца
.
Характер изменения температуры при установлении квазистационарного температурного режима показан на рис.1.
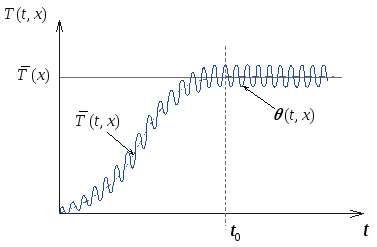
Рис. 1 Установление квазистационарного состояния при периодическом нагреве.
– кривые
изменения гладкой и осциллирующей
составляющей решения
во времени,
– стационарная составляющая температурного
поля,
– время выхода на квазистационарный
тепловой режим.
При
(в дальнейшем при
)
осциллирующую и гладкую части решения
можно рассматривать раздельно, причем
в силу линейности задачи осциллирующая
часть решения имеет ту же частоту, что
и внешнее воздействие
. (1.17)
Решение уравнения (1.3) с граничным условием (1.7) для осциллирующей части имеет вид
(1.18)
и получается подстановкой (1.4) и (1.17) в исходное уравнение.
Здесь
возникает новый параметр
,
обратная величина которого известна
как критерий Био. Если
,
то соотношение (1.18) с хорошим приближением
переходит в
(1.19)
Решения
(1.18), (1.19) описывают температурную волну,
распространяющуюся с фазовой скоростью
.
Амплитуда температурной волны
экспоненциально падает с увеличением
частоты
.
Так как коэффициент затухания
на частотах, превышающих
весьма велик, то на толщине
большинство материалов непрозрачны
для высокочастотных температурных
волн.
Из полученного решения следует, что средний поток за период
равен нулю.
Исходные данные:
— количество
членов суммы ряда
— коэффициент
теплопроводности (см2/с)
= 0,0162 —
линеаризованный коэффициент теплопотерь,
[Вт/см2]
= 3,27 —
тепловая активность [(Дж/см2*К)2/с]
l — толщина пластины, [см]
= 0 —
наблюдаем изменение формы пульсаций
на поверхности образца
tp — период колебаний, [c]
ti —длительность импульса, [c]
Листинги программ исследований
script % конфигурации температурного поля при различных способах нагрева
% =========================================================================
%
% параметры константы
a=0.0162; % коэффициент температуропроводности, [см^2/c]
alfa=0.318; % линеаризованный коэффициент теплопотерь, [Вт/см^2]
D=3.2; % тепловая активность [(Вт/см^2 K^2)*c]
l=0.001; % толщина пластины, [см]
x=0 % наблюдаем изменение формы пульсаций на поверхности образца
x =
0
% импульсный нагрев
tp=1e-6; % период колебаний, [c]
ti=tp/20; % длительность импульса, [c]
t=0:ti/100:tp; % задаём временной интервал от 0 до tp в долях ti, [c]
N=10000; % количество цленов суммы ряда
Hsur=plot(t,normalize_v(real(q1(N,t,ti,tp))),'r',t,normalize_v(teta12(N,x,l,a,alfa,D,t,ti,tp)),'b');
set(Hsur, 'LineWidth', 3);
ylabel('T(x,t), q(t)');