
Матанализ_билеты_20.12.15
.pdf
Собрал Мигалин Сергей, версия от 20.12.15 (с 11 билетом)
Математический анализ
Экзамен 2 модуль
Версия от 20.12.15 (с 11 билетом)
УТОЧНИТЕ ДЛЯ ОКОНЧАТЕЛЬНОЙ ВЕРСИИ!!!
1)Билет 51 и 57 – одинаковые теоремы? Или есть какой-то другой вывод?
Присоединяйтесь к решению задач экзамена!
Внести свою лепту можно тут: https://vk.com/board108789813
1.Дать определения множества, ограниченного сверху (снизу), ограниченного множества. Доказать эквивалентность двух определений ограниченного множества.
Множество X ограничено сверху, если |
|
|
|
C |
|
Множество ограничено снизу, если |
|||||
I. |
Множество X ограничено, если |
C: x X|x| |
|||
|
|
|
|||
II.Множество Х называется ограниченным, если оно ограничено сверху и снизу.
2.Дать определения верхней и нижней граней множества. Привести примеры ограниченных сверху (снизу) множеств, содержащих и не содержащих свою верхнюю (нижнюю) грань. Сформулировать теорему о существовании верхней (нижней) грани у множества.

Собрал Мигалин Сергей, версия от 20.12.15 (с 11 билетом)
Примеры:
Теорема. Ограниченное сверху (снизу) непустое множество имеет верхнюю (нижнюю) грань.
3.
1. lim
→
|
0 |
| |
| |
или
2. lim ∞
→
0 |
|
∞ |
или |
|
3. lim ∞
→
0 |
|
∞ |
или |
|
4.Доказать ограниченность последовательности, имеющей конечный предел. Показать на примерах, что обратное утверждение неверно.

Собрал Мигалин Сергей, версия от 20.12.15 (с 11 билетом)
Теорема, обратная доказанной, не имеет места, т.е. не всякая ограниченная последовательность имеет предел.
5.Дать определения бесконечно большой и бесконечно малой последовательностей. Привести примеры.
1. |
Последовательность бесконечно малая, если |
|
0 |
||
2. |
Последовательность бесконечно большая, |
если |
|||
|
lim→ |
||||
|
lim→ | | |
∞ |
|
|
|
6.Доказать теорему Вейерштрасса о существовании предела у неубывающей ограниченной сверху последовательности. Сформулировать варианты этой теоремы.
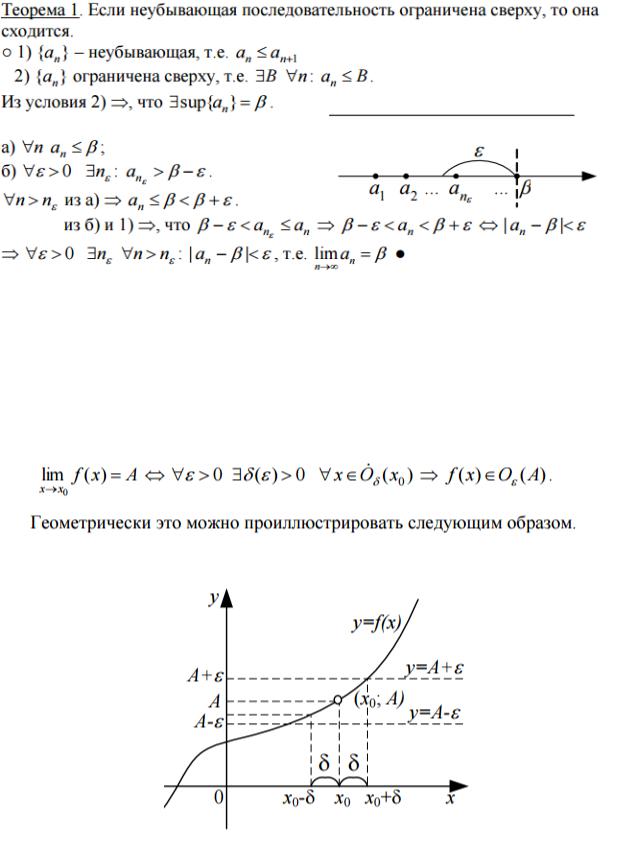
Собрал Мигалин Сергей, версия от 20.12.15 (с 11 билетом)
Варианты теоремы:
Если невозрастающая последовательность ограничена снизу, то она сходится.
Монотонная ограниченная последовательность сходится
7.Сформулировать следующие определения пределов (при помощи неравенств и при помощи окрестностей)
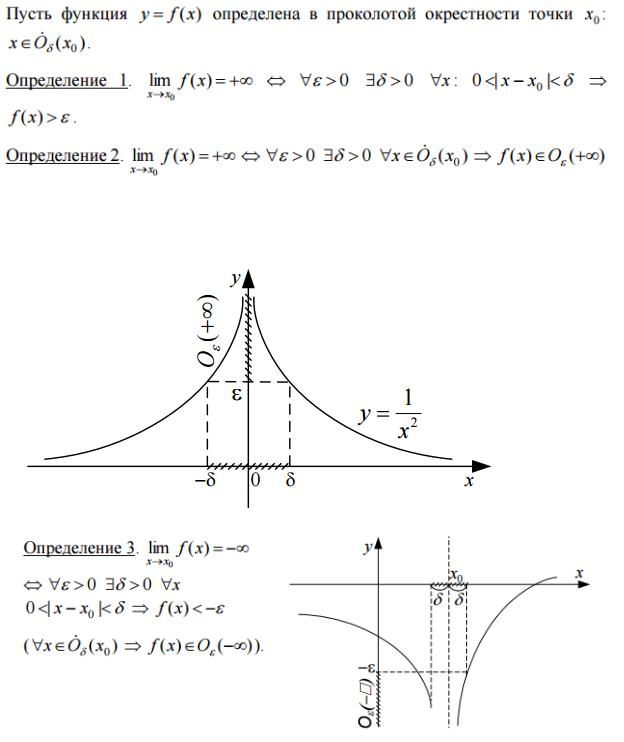
Собрал Мигалин Сергей, версия от 20.12.15 (с 11 билетом)
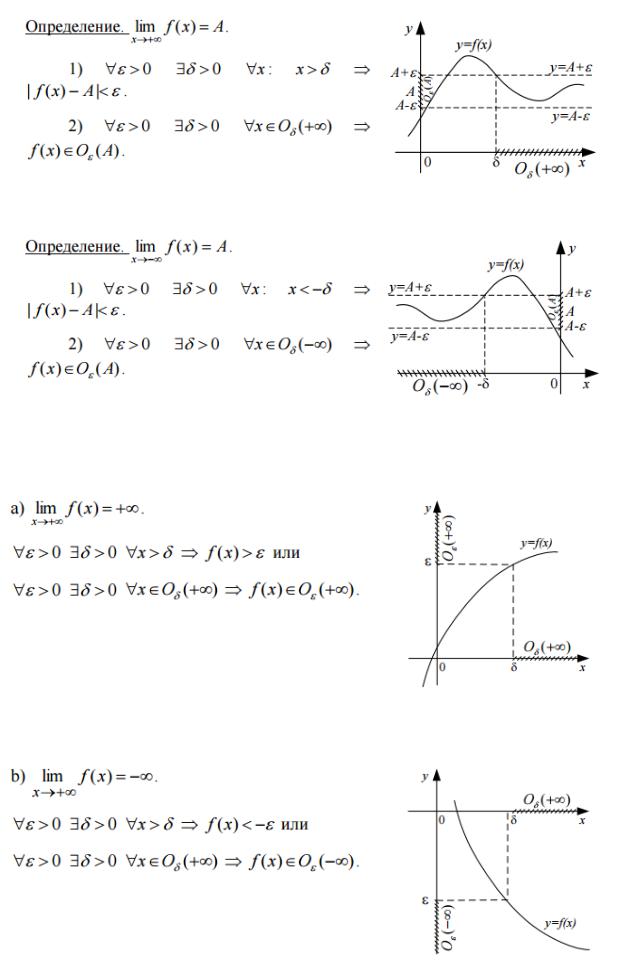
Собрал Мигалин Сергей, версия от 20.12.15 (с 11 билетом)

Собрал Мигалин Сергей, версия от 20.12.15 (с 11 билетом)
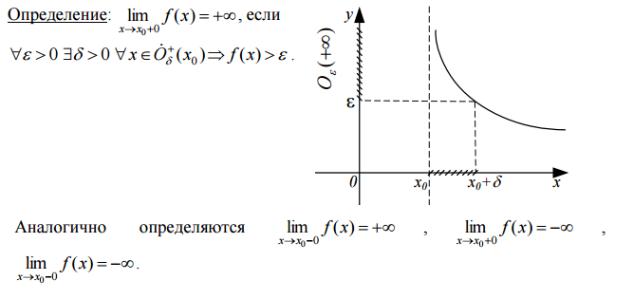
Собрал Мигалин Сергей, версия от 20.12.15 (с 11 билетом)

Собрал Мигалин Сергей, версия от 20.12.15 (с 11 билетом)
8.Дать определение бесконечно малой функции при x->x0. Доказать теорему: функция f(х) имеет предел b тогда и только тогда, когда величина f(х) – b – бесконечно малая.

Собрал Мигалин Сергей, версия от 20.12.15 (с 11 билетом)
9.Доказать теорему о локальной ограниченности функции, имеющей конечный предел.
