2042

Следует иметь в виду, что 0! 1; 1! 1; Cn0 1; Cnn 1; Cnm Cnn m.

П р и м е р . В полуфинале первенства России по шахматам участвуют 20 шахматистов, а в финал попадают трое. Сколькими способами может образоваться финальная тройка?

Решение.

Надо подсчитать число соединений, которые можно составить из 20 элементов по три элемента, причем каждое соединение отличается от другого только составом (порядок элементов в каждой тройке не важен). Поэтому эти соединения являются сочетаниями, и их число

секретаря и трех членов редакционной комиссии. Сколькими способами это можно сделать?

Решение.

Из 80 человек председателя можно выбрать 80 способами, т.е. число способов равно C801 80.

Число способов выбора секретаря из оставшихся 79 человек равно C791 79. Число способов выбора трех членов редакционной

комиссии из оставшихся 78 человек равно C783 , тогда, по правилу

произведения, число способов выбора из 80 человек председателя, секретаря и трех членов редакционной комиссии равно

Широко известные формулы сокращенного умножения квадрата суммы и разности, куба суммы и разности являются частными случаями бинома Ньютона. Когда степень бинома невысока, коэффициенты многочлена могут быть найдены не расчетом по формуле количества сочетаний, а с помощью так называемого

треугольника Паскаля (Блез Паскаль (1623 – 1662) – французский математик).

Этот треугольник имеет вид

Формула бинома Ньютона может быть обобщена для произвольного числа слагаемых.

n1 n2 ... nk n.

Напомним, что при вычислениях 0! принимается равным 1. Пример. В разложении xk y p n найти члены, содержащие х ,

В принципе можно написать разложение этого выражения в многочлен, определить коэффициенты либо непосредственно, либо из треугольника Паскаля (степень бинома сравнительно невелика), однако делать это не обязательно, т.к. необходимо найти только член

Для нахождения полного разложения необходимо определить все возможные значения ni, это связано с громадными вычислениями. Однако, т.к. надо найти только члены, содержащие х6, то n1 = 6, а сумма всех четырех значений п равна 9, значит, сумма п2 + п3 + п4 = 3. Рассмотрим возможные значения этих величин (табл. 2.1).

Таблица 2.1

Искомые члены разложения:

Контрольные вопросы

1.Что такое комбинаторика?

2.Перечислите правила комбинаторики.

3.Что называется перестановкой, размещением, сочетанием из n элементов по m элементов?

4.В чем отличие размещений от перестановок, сочетаний от размещений?

5.Запишите формулу бинома Ньютона.

Упражнения

1.Города А и В соединены один с другим тремя различными дорогами. 1). Сколькими способами можно совершить круговой рейс от А к В и обратно? 2). Сколько будет таких способов, если на обратном пути обязательно избирать новую дорогу?

2.Номер автомобиля состоит из трех букв русского алфавита (33 буквы) и четырех цифр. Сколько существует различных номеров автомобилей? (Номер 0000 возможен, буквы могут повторяться.)

3.Бросаются две игральные кости. Сколько возможных комбинаций пар очков будет?

4.Буквы азбуки Морзе состоят из последовательности точек и тире. Сколько букв можно изобразить, если потребовать, чтобы каждая буква содержала не более пяти символов?

5.Сколько различных чисел, не содержащих одинаковых цифр, можно написать при помощи цифр 1, 2, 3, 4, 5, 6, 7, 8, 9?

6.Скольким числом способов можно расположить для фотографирования 5 человек, если троих поставить в передний ряд, а двух сзади?

7.Сколько различных четырехзначных чисел, делящихся на 4, можно составить из цифр 1, 2, 3, 4, 5, если каждую из них можно использовать не более одного раза?

8.10 групп занимаются в десяти подряд расположенных аудиториях. Сколько существует вариантов расписания, при которых группы №1 и 2 находились бы в соседних аудиториях?

9.В учебном плане 10 учебных дисциплин и три разных дисциплины

можно назначить в день. Сколькими способами могут быть распределены дисциплины в день?

Расчетно-графическая работа по разделу «Элементы комбинаторного анализа»

Вариант 1

1.Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти различных оттенков?

2.Сколькими способами можно построить в одну шеренгу игроков двух футбольных команд так, чтобы при этом два футболиста одной

команды не стояли рядом?

Вариант 2

1.Сколькими способами можно выбрать гласную и согласную из слова «студент»?

2.Группа студентов изучает восемь различных дисциплин. Скольким числом способов можно составить расписание занятий в субботу, если в этот день недели должно быть три различных дисциплины (порядок дисциплин роли не играет)?

Вариант 3

1.Сколькими способами можно составить флаг, состоящий из четырех горизонтальных полос, имея четыре различных цвета?

2.Из группы в 15 человек должны быть выделены бригадир и 4 члена бригады. Сколькими способами это можно сделать?

Вариант 4

1.Четверо студентов получают оценки A, B, C, D. Сколькими различными способами можно расставить оценки так, чтобы никакие два студента не получили одну и ту же оценку?

2.В урне 10 белых и 5 черных шаров. Сколькими способами из урны наугад можно вынуть три шара, чтобы при этом два шара оказались белыми, а один – черным?

Вариант 5

1.Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что числа могут содержать одинаковые цифры? 2.Скольким числом способов можно распределить шесть пригласительных билетов на презентацию среди 30 человек?

Вариант 6

1.Из пункта А в пункт В можно добраться самолетом, поездом и автобусом, причем между этими пунктами существуют два авиамаршрута, один железнодорожный и три автобусных. Скольким

числом способов можно добраться из А в пункт В?

2. Комиссия состоит из председателя, его заместителя и еще пяти человек. Сколькими способами члены комиссии могут распределить между собой обязанности?

Вариант 7

1.Сколькими различными способами можно распределить четыре шара по двум лункам, в которые помещается ровно один шар?

2.Сколько различных аккордов можно взять на 10 выбранных клавишах рояля, если каждый аккорд может содержать от трех до пяти звуков?

Вариант 8

1.Сколькими способами можно разложить пять монет различного достоинства по трем карманам?

2.Из 10 кандидатов на одну и ту же должность должны быть выбраны трое кандидатов. Сколько может быть разных случаев выборов?

Вариант 9

1.Сколько может быть номеров телефона, если известно, что они пятизначные? (Считается, что номера 00000 и 99999 возможны.)

2.В хирургическом отделении работают 40 врачей. Сколькими способами из них можно организовать бригаду в составе хирурга и ассистента?

Вариант 10

1.Сколько различных способов распределения 8 студенческих путевок между тремя студенческими группами существует, если все путевки различны?

2.На тренировках занимаются 12 баскетболистов. Сколько может быть образовано тренером стартовых пятерок?

Вариант 11

1. Пять студентов следует распределить по трем группам факультета.

Скольким числом способов это можно сделать?

2. В группе 25 студентов. Из них 6 человек надо посадить на первый ряд. Сколько имеется таких способов, если не обращать внимания на порядок, в котором студенты сидят на скамейке, а только на фамилии их?

Вариант 12

1.Три автомобиля, №1, 2, 3, должны доставить товар в шесть магазинов. Сколькими способами это можно сделать, если грузоподъемность каждого из них позволяет взять товар сразу для всех магазинов и если два автомобиля в один и тот же магазин не направляются?

2.Шесть человек рассаживаются на скамейке. Скольким числом способов это можно сделать так, чтобы два определенных человека оказались рядом?

Вариант 13

1.Сколько существует трехзначных номеров студенческих билетов, не содержащих цифры 8?

2.Четыре стрелка должны поразить 8 мишеней, по две каждый. Сколькими способами они могут распределить мишени между собой?

Вариант 14

1.Шесть пассажиров наудачу рассаживаются в трех вагонах. Скольким числом способов это можно сделать?

2.Вам надо выбрать два факультатива из 6. Скольким числом способов это можно сделать?

Вариант 15

1.Сколько различных трехзначных чисел, делящихся на 3, можно составить из цифр 0, 1, 2, 3, 4, 5, если каждое число не должно содержать одинаковых цифр?

2.Скольким числом способов можно выбрать три красных и два черных шара, если в коробке находится 7 красных и 5 черных шаров?

Вариант 16

1.Буквы азбуки Морзе образуются как последовательности точек и тире. Сколько различных букв можно образовать, если использовать 5 символов?

2.Из колоды, содержащей 36 карт, наугад вытаскивают 5 карт. Сколько существует таких наборов, в которых содержится три туза?

Вариант 17

1.Сколько существует различных семизначных номеров телефона? (Телефонный номер может начинаться с нуля.)

2.На собрании присутствуют 40 человек. Необходимо избрать председателя, секретаря и двух членов президиума. Скольким числом способов это можно сделать?

Вариант 18

1.Сколько различных трехзначных чисел может быть составлено из цифр 1, 2, 3, 4, 5, если в каждом числе нет одинаковых цифр?

2.Вам надо выбрать два факультатива из шести. Скольким числом способов это можно сделать, если занятия на двух факультативах начинаются с 10 часов, еще двух других – с 12 часов, а остальные не пересекаются во времени?

Вариант 19

1.Сколько существует натуральных чисел, меньших 104, в записи которых в десятичной системе все числа различны?

2.Из слова «дом» перестановками букв можно получить слова «дмо», «одм», «мдо», «омд», «мод», которые называют анаграммами. Сколько анаграмм можно получить из слова «полдень»?

Вариант 20

1.Сколько существует различных трехцветных флагов с тремя вертикальными полосами одинаковой ширины, если можно использовать материю семи цветов?

2.Вам надо выбрать два факультатива из шести. Скольким числом

способов это можно сделать, если два факультатива совпадают по времени?

Вариант 21

1.Сколько четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, если каждое из них можно использовать не более одного раза?

2.В ящике 12 деталей, из которых 4 окрашены. Скольким числом способов можно из ящика выбрать три детали таким образом, чтобы среди них было две окрашенных?

Вариант 22

1.Сколько можно образовать целых чисел, из которых каждое изображалось бы тремя различными цифрами?

2.На станке должны быть последовательно обработаны пять различных деталей. Сколько вариантов должен проанализировать технолог для выбора наилучшей очередности их обработки?

Вариант 23

1.Сколько различных способов распределения шести пирожных между тремя людьми, если все пирожные разные?

2.Сколькими способами можно рассадить группу студентов из 25 человек в аудитории, имеющей 30 мест?

Вариант 24

1.Сколько существует шестизначных чисел, делящихся на пять?

2.Десять книг расставляются на одной полке. Сколькими способами их можно расставить так, чтобы при этом две определенные книги оказались рядом?

Раздел 3. ГРАФЫ И СЕТИ

Лекция 3.1. Основные понятия и определения

Историческая справка. Элементы графа. Ориентированные и

неориентированные графы. Маршруты, цепи, циклы. Достижимость и связность. Способы задания графов. Операции над графами.

Историческая справка

Теория графов – область дискретной математики, особенностью

которой является геометрический подход к изучению объектов.

Первые задачи теории графов были связаны с решением

математических развлекательных задач и головоломок. Среди них

важную роль в теории графов сыграли следующие три задачи.

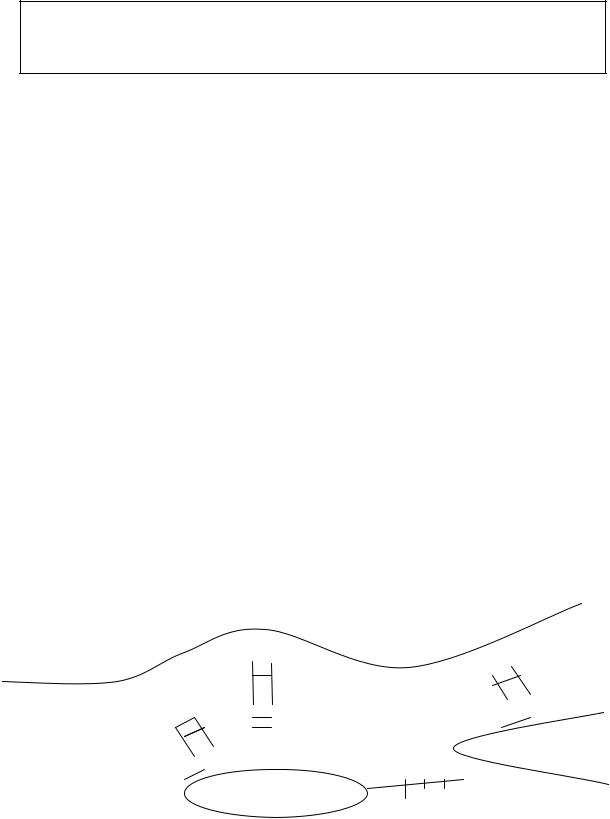
1. Задача о кенигсбергских мостах .

На рис. 3.1 схематично изображена карта города Кенигсберга в XVIII в. (ныне г. Калининград). Город расположен на берегах и двух островах реки Преголи. Острова между собой и с берегами были связаны семью мостами. Требовалось ответить на вопрос: можно ли, выйдя из дома, вернуться обратно, проходя по каждому мосту ровно один раз?