2042

Лекция 1.3. Соответствия

Соответствия и их свойства. Функции и отображения. Алгебраические

структуры.

Соответствия и их свойства

Соответствие – способ задания взаимосвязей, взаимодействий между элементами множества (наряду с отношениями).

Частные случаи соответствий: функции отображения, преобразования, операции и др.

Соответствием между множествами А и В называется

соответствии G ».

Областью определения соответствия G называется множество

G1 a : a,b G .

Областью значений соответствия G называется множество

G2 b : a,b G (рис. 1.13).

G

B

A

G1 G2

Рис. 1.13

Основные свойства соответствий G A B:

1.Всюду (полностью) определенное соответствие, если G1 A, и частично определенное соответствие, если G1 A.

2.Сюръективное соответствие, если G2 B .

Образом элемента a в множество В при соответствии G называется множество всех b B , соответствующих элементу a A.

единственный элемент a G1.

При взаимно-однозначном соответствии мощности двух множеств А и В равны, т.е. A B , говорят, что множества А и В

равномощны.

При м ер . Дано множество G – множество пар действительных чисел x, y , удовлетворяющих соотношению x 1 2 y 3 2 1.

оси OY ). Образом числа 2 G1 (на оси OX ) является число 3 G2 (на

оси OY ).

3. Прообраза числа 0 (на оси OY ) не существует. Не существует

действительных чисел отрезка 0;2 G1 (на оси OX ). Прообразом2,4 (на оси OY ) является множество действительных чисел отрезка0;2 G1 (на оси OX ).

Функции и отображения

Функцией называется функциональное соответствие. Если функция f устанавливает соответствие между множествами А и В, то

применяются обозначение f:A B f a b, где элемент a

аргумент; элемент b значение функции на a .

Отображением А в В называется всюду определенная функция f:A B .

Отображением А на В называется всюду определенное

Способы задания функции: 1) графиком; 2) таблицей;

3) формулой, описывающей функцию как суперпозицию исходных функций;

4) рекурсивной вычислительной процедурой.

Например, функция f x x! при f 0 1; f x 1 f x x 1 .

Операции

Операцией называют функцию, все аргументы и значения которой принадлежат одному и тому же множеству.

n -местная функция типа : A A A ... A A или : An A

называется n -арной операцией на множестве A.

Говорят, что множество A замкнуто относительно операции .

Частные случаи:

1. Функция одного аргумента x y , имеющая тип : A A,

называется унарной операцией.

Примеры унарных операций:

а) элементарные функции: ex , log a x , sin x , cos x и др.;

б) операция дополнение множества A ;

в) отображение типа A A-преобразования, перестановки и др.

2.Функция двух аргументов x, y z , имеющая тип

: A A A, называется бинарной операцией.

Примеры:

а) арифметические операции: сложение, вычитание, умножение, деление, возведение в степень;

б) операции над множествами: пересечение , объединение , разность \.

Свойства бинарных операций:

1) ассоциативна, если для a,b,c Aa b c a b c ,

арифметические операции сложения и умножения, операции объединения и пересечения множеств, композиция отображений – ассоциативные операции;

2) коммутативна, если для a,b,c a b b a ,

арифметические операции сложения и умножения, операции объединения и пересечения множеств – коммутативные операции;

3) дистрибутивна слева относительно операции , если для

a,b,c выполняется a b c a b a c ,

дистрибутивна справа относительно операции , если для

a,b,c выполняется a b c a c b c ,

арифметические операции умножения и деления дистрибутивны относительно операций сложения и вычитания слева и справа, но не наоборот.

Способы задания операций

Операция является функцией, поэтому она задается теми же

2.Способы задания бинарных операций : A A A на конечном множестве A a1,a2,...,an :

а) таблицей Кэли – это квадратная таблица умножения, в которой слева и сверху выписывают все значения аргументов a и b из множества A соответственно, на пересечении соответствующих строк и столбцов записывают результат c – операции над a и b ;

б) списком всех троек a,b,c , где a,b – соответственно первый и второй аргументы из A; c – результат выполнения операции над a

и b ; a,b,c A.

Для всюду определенной операции число всех троек в списке

A A n2 ;

в) формулой a,b c – префиксное представление операции. Формулой a b c – инфиксное представление операции.

При м ер . Являются ли бинарные алгебраические операции ассоциативными?

Решен и е .

1. Для операции сложения

a b c a b c 2 3 4 2 3 4 .

Для операции умножения

a b c a b c 2 3 4 2 3 4

операции сложения и умножения ассоциативны. 2. Для операции вычитания

a b c a b c 5 3 4 5 3 2 .

Для операции деления

a : b : c a : b : c 10 : 5 : 2 10 : 5: 2 .

Для операции возведения в степень

ab c a bc ,abc abc 22 3 2 23 .

Таким образом, операции вычитания, деления, возведения в степень неассоциативны.

П р и м е р . Установить являются ли бинарные операции над множествами ассоциативными.

Решен и е .

1.Для операции объединения множеств A B C A B C .

Иллюстрация справедливости данного соотношения на множествах:

A a,b,c ; B b,c,d ; c b,d .

Левая часть:

A B C a,b,c b,c,d b,d a,b,c,d b,d a,b,c,d .

Правая часть:

A B C a,b,c b,c,d b,d a,b,c b,c,d a,b,c,d . 2.Для операции пересечения множеств A B C A B C .

Иллюстрация на множествах A a,b,c ; B b,c,d ; c b,d .

Левая часть:

A B C a,b,c b,c,d b,d b,c b,d b .

Правая часть:

A B C a,b,c b,c,d b,d a,b,c b,d b .

Операции объединения и пересечения множеств ассоциативны. 3.Для операции разности множеств A \ B \ C A \ B \ C .

Иллюстрация на множествах: A a,b,c ; B b,c,d ; c b,d .

Левая часть:

A \ B \ C a,b,c \ b,c,d \ b,d a \ b,d a .

Правая часть:

A \ B \ C a,b,c \ b,c,d \ b,d a,b,c \ c a,b , т.е. получили

a a,b операция вычитания множеств неассоциативна.

Алгебраические системы

Пусть дано множество A.

Алгеброй называется совокупность множества A с заданными в ней операциями S 1, 2,..., n , обозначается A,S.

Множество A называется носителем, а S сигнатурой алгебры. Группоидом называется алгебра, сигнатура которой состоит из

одной операции и обозначается A,*, где символ « » обозначает только одну операцию на множестве A.

Группоид называют мультипликативным, если « » операция умножения, и аддитивным, если « » операция сложения.

Для алгебры (или группоида) можно ввести единичный элемент e, для которого справедливо: a e e a.

Если группоид 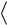A, мультипликативный, единичный элемент называется «единица» и обозначается «1».

Если группоид A, 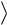аддитивный, единичный элемент называется

«нуль» и обозначается «0».

Обратным элементом алгебры (или группоида) называется

элемент a 1, который удовлетворяет условиям a a 1 a 1 a e. Множество A вместе с заданными операциями 1, 2,..., n и

отношениями T1,T2,...,Tn называется алгебраической системой

или алгебраической структурой.

Обозначение алгебраической структуры:

A; 1, 2,..., n;T1,T2,...,Tn .

При м ер . Рассмотрим множество положительных рациональных чисел с операцией умножения. Единичным элементом является «1». Каждому положительному рациональному числу x можно поставить

всоответствие обратный элемент 1x , который обеспечивает

выполнение условия x 1x 1x x 1.

Группоид A, , для любых элементов a1,a2,a3 которого

выполняется закон ассоциативности

a1 a2 a3 a1 a2 a3 ,

называется полугруппой.

При м ер . Множество целых чисел n является полугруппой по

операции умножения, так как для любых трех целых чисел

выполняется ассоциативный закон. Например, 2 3 4 2 3 4 .

Группоид A, называется группой, если для любых элементов a1,a2,a3 выполняются условия:

1)закон ассоциативности: a1 a2 a3 a1 a2 a3 ;

2)в множестве A существует единичный элемент e :

a e e a a;

3) в множестве A для любого элемента a существует

обратный элемент a 1.

Пример. Рассмотрим множество целых чисел n . Введем в это множество операцию умножения.

1.Операция умножения ассоциативна.

2.Существует единичный элемент 1: n 1 1 n n .

3.Обратный элемент n 1 является также целым числом не для

всех целых чисел, например, для числа 2 обратный элемент 1 не

2

является целым числом.

Таким образом, множество целых чисел не является группой по умножению.

Пример. Рассмотрим множество векторов на плоскости R2 , в

которое введена операция сложения.

1.Операция сложения векторов ассоциативна, т.е.a b c a b c .

2.Единичным элементом будет нулевой вектор 0 , так как

a a a a 0 получили единичный вектор.

Таким образом, множество векторов на плоскости R2 является

группой по сложению.

Замечание. Различные множества могут являться группой относительно какой-либо операции и не являться группой относительно другой.

Если операция, определенная в группе, коммутативна, то такая группа называется коммутативной или абелевой группой.

Рассмотрим множества A и B . Пусть между множествами A и B

Таким образом, имеем две алгебры: A; и B; .

Отображение G : A B называется гомоморфизмом алгебры

A; в алгебру B; , если выполняется условие

G a b G a G b .

изоморфными.

Рассмотрим алгебру, в которой определены операции сложения и умножения A; , .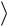

Если для любых элементов a1,a2,a3 множества A выполняются 1) закон коммутативности: a1 a2 a2 a1;

2) закон ассоциативности:

a1 a2 a3 a1 a2 a3 ; 3) закон дистрибутивности:

a1 a2 a3 a1 a2 a1 a3;a1 a2 a3 a1 a3 a2 a3,

то алгебра A; , называется кольцом.

Кольца, в которых для всех ненулевых элементов существуют обратные, называются телами.

При м ер . Тело не является группой по операции умножения, так как обратные элементы существуют только для ненулевых элементов.

При м ер . Множество рациональных чисел R является телом.

Тело называется полем, если оно обладает свойством коммутативности по операции умножения, т.е. a1 a2 a2 a1.

Контрольные вопросы

1.Что называется соответствием?

2.Что называется областью определения и областью значений соответствия?

3.Основные свойства соответствий G A B .