
2042
.pdf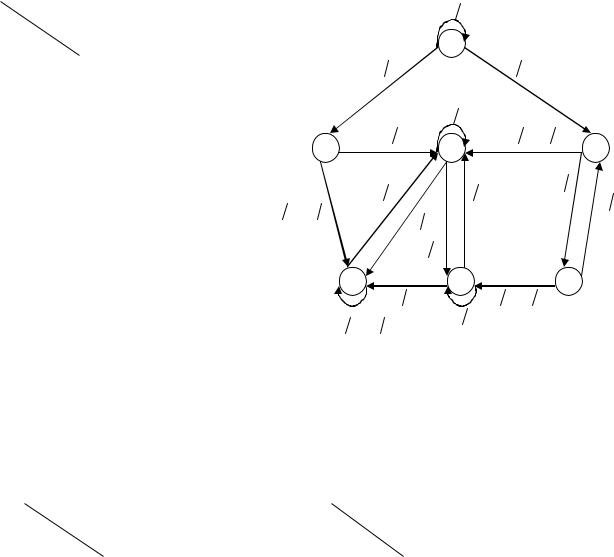
2. |
Задана общая таблица переходов автомата: |
|
|
|||||||
|
|
|
|
|
|
|
|
|
0 1 |
|
|
x |
|
0 |
|
1 |
2 |
|
|
|
|
s |
|
|
|
|
|
|
|
3 |
|
|
0 |
|
|
1/1 |
|
4/0 |
4/1 |
|
2 1 |
|
1 0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
5/1 |
|
1/1 |
4/1 |
|
|
1 1 |
|
|
|
|
|
|
|
|
|
0 1 |
0 0 1 1 |
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
1/0 |
|
1/1 |
6/1 |
|
|
||
|
|
|
0 |
|
1 |
2 |
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2 1 |
3 |
|
|
3/1 |
|
2/0 |
0/1 |
|
0 1 |
0 0 |
|
|
|
|
|
|
|
|
1 0 2 1 |
2 1 |
||
|
|
|
|
|
|
|
|
|
||
4 |
|
|
1/1 |
|
4/0 |
4/1 |
2 1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
0 1 |
|
|
5 |
|
|
1/0 |
|
5/1 |
4/1 |
|
|
6 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
4 |
|
5 |
|
6 |
|
|
5/0 |
|
5/1 |
2/1 |
2 1 |
0 0 1 1 |
||
|
|
|
|
1 1 |
||||||
|
|
|
|
|
|
|
1 0 2 1 |
|
||
|
|
|
|
|
|
|
|
|
||
|
Убедиться, что граф этого автомата имеет вид, представленный |
|||||||||
на рисунке рядом с таблицей. |
|
|
|
|
||||||
3. |
Для автомата, заданного в задаче 2, убедиться, что пары состояний |
|||||||||
0;4 и |
1;5 |
являются эквивалентными. |
Объединяя эквивалентные |
|||||||
состояния в заданном автомате, получить последовательно таблицы переходов:
x |
0 |
1 |
2 |
s |
|
|
|
0(4) |
1/1 |
0/0 |
0/1 |
|
|
|
|
1(5) |
1/0 |
1/1 |
0/1 |
|
|
|
|
2 |
1/0 |
1/1 |
6/1 |
|
|
|
|
3 |
3/1 |
2/0 |
0/1 |
|
|
|
|
6 |
1/0 |
1/1 |
2/1 |
|
|
|
|
x |
0 |
1 |
2 |
s |
|
|
|
0(4) |
1/1 |
0/0 |
0/1 |
|
|
|
|
1(5) |
1/0 |
1/1 |
0/1 |
|
|
|
|
2(6) |
1/0 |
1/1 |
2/1 |
|
|
|
|
3 |
3/1 |
2/0 |
0/1 |
|
|
|
|
Построить граф, соответствующий сокращенному автомату с четырьмя состояниями (т. е. последней таблице переходов).
Лекция 5.2. Введение в теорию алгоритмов

Понятие алгоритма. Рекурсивные функции. Простейшие (базисные) функции.
Операторы. Машины Тьюринга.
Понятие алгоритма
Понятие алгоритма возникло в математике ещё в древние времена и происходит, как предполагают, от algorithmi – латинского написания арабского имени среднеазиатского математика IX в. аль-Хорезми.
Алгоритм – точное предписание, которое задает вычислительный процесс (называемый в этом случае алгоритмическим), начинающийся с произвольного исходного данного (из некоторой совокупности возможных для данного алгоритма исходных данных) и направленный на получение полностью определяемого этим исходным данным результата.
Салгоритмами математика имела дело всегда. Школьные методы умножения «столбиком» и деления «углом», метод исключения неизвестных при решении систем линейных уравнений, правило дифференцирования сложной функции, способ построения треугольника по трём данным сторонам – всё это алгоритмы.
Сточки зрения современной практики алгоритм – это программа,
акритерием алгоритмичности процесса является возможность его запрограммировать.Однако все данные выше пояснения понятия «алгоритм» являются интуитивными. Понятие алгоритма относится к фундаментальным неопределяемым понятиям. Поэтому попробуем «уточнить» это понятие с помощью характеризующих его основных признаков, сформулировав их как основные требования к алгоритмам или основные свойства алгоритма.
1. Для каждого алгоритма существует совокупность исходных данных – объектов, к которым имеет смысл применять рассматриваемый алгоритм.
Очевидно, что эти объекты должны быть чётко определены и отличимы друг от друга, а также от того, что не является объектом. К таким алгоритмическим объектам относятся, например, числа, векторы, матрицы, формулы, а также некоторые другие чётко определенные объекты.
Кроме исходных данных каждый алгоритм имеет дело с
промежуточными и выходными данными.
Таким образом, для данного алгоритма можно выделить совокупность возможных исходных данных, совокупность возможных промежуточных результатов, совокупность возможных.
2.Алгоритм состоит из отдельных элементарных шагов, множество которых конечно. Это требование (свойство) обычно называют дискретностью алгоритма.
Система команд компьютера – типичный пример такого множества элементарных шагов.
3.Последовательность шагов алгоритма должна быть точно определена. Это означает, что совокупность промежуточных данных на каждом шаге однозначно определяется совокупностью промежуточных данных, полученных на предыдущем шаге. Таким образом, после каждого шага указывается, какой шаг делать далее. Эту характеристику (требование) называют детерминированностью
алгоритма. Она обеспечивает однозначность результата при заданных исходных данных.
4.Алгоритм через конечное число шагов должен привести к остановке, которая свидетельствует о достижении требуемого результата (или с указанием того, что считать результатом). Это требование (свойство) называют результативностью алгоритма.
5.Алгоритм служит для решения всех задач данного класса (типа), причём совокупность исходных данных может выбираться из некоторого множества. Это требование (свойство) называют
массовостью алгоритма.
Например, алгоритм нахождения обратной матрицы должен быть применим к любой матрице порядка n .
Алгоритмы, которые сводят решение поставленной задачи к арифметическим действиям над числами, называют численными алгоритмами. В качестве примера приведем известный алгоритм Евклида для нахождения наибольшего общего делителя двух заданных целых положительных чисел a и b .
Алгоритм Евклида состоит из следующей последовательности шагов (указаний):
1)обозревай a и b и переходи к следующему;
2)сравни обозреваемые числа ( a b, или a b , или a b) и переходи к следующему;
3)если обозреваемые числа равны, то каждое из них дает искомый результат, если нет – переходи к следующему;
4)если первое обозреваемое число меньше второго, переставь их местами и переходи к следующему;
5)вычитай второе число из первого и обозревай два числа – вычитаемое и остаток, переходи к указанию 2.
Из представленного алгоритма видно, что после пятого указания следует каждый раз возвращаться ко второму до тех пор, пока не будет выполнено третье указание. Заранее неизвестно, сколько потребуется таких переходов, но очевидно, что для любых двух чисел цель будет достигнута за конечное число шагов.
Численные алгоритмы имеют широкое распространение благодаря тому, что к ним сводится решение многих задач, например, решение систем линейных уравнений, вычисление корней алгебраических уравнений, численное дифференцирование и т.д.
Существуют и другие типы алгоритмов, в частности логические алгоритмы, которые содержат предписания, относящиеся не к цифрам, а к объектам любой природы. Примером такого логического алгоритма может служить алгоритм поиска пути в конечном лабиринте.
В середине 30-х гг. XX в. были предприняты попытки формализовать понятие алгоритма. Понятие алгоритма заменили строго формализованными математическими моделями. Среди самых известных рекурсивные функции, машины Тьюринга и нормальные алгорифмы Маркова. Эти математические модели эквивалентны в том смысле, что классы решаемых ими задач совпадают. Этот принцип, высказанный А. Чёрчем в 1936 г., носит название тезиса Чёрча, который подтверждён опытом, накопленным в математике за всю её историю. Все известные в математике алгоритмы удовлетворяют ему. Таким образом, для любой алгоритмически разрешимой задачи можно построить рекурсивную функцию (машину Тьюринга, нормальный алгоритм Маркова), и наоборот, для задач, для которых нельзя построить указанные выше модели, не существует алгоритма решения.
Формальное определение алгоритма дало возможность развивать теорию алгоритмов. Основная задача классической теории алгоритмов – это ответ на вопрос, являются ли задачи данного класса алгоритмически разрешимыми, т. е. можно ли для задач данного типа построить алгоритм, решающий эти задачи. Отметим, что в ряде случаев на этот вопрос теория алгоритмов дает отрицательный ответ. Помимо установления алгоритмической разрешимости задач теория
алгоритмов занимается оценкой сложности алгоритмов и создания эффективных алгоритмов.
Рекурсивные функции
Поскольку всякий алгоритм исходным данным, на которых он определён, ставит в соответствие результат, то можно сказать, что с каждым алгоритмом связана функция, которую он вычисляет. Тогда возникают вопросы: для каких функций алгоритмы существуют и как описать такие алгоритмически вычислимые функции?
Исследование этих вопросов привело к созданию в 30-х гг. прошлого века теории рекурсивных функций. Рекурсивные функции основаны на той идее, что исходные данные и возможные результаты решения любой задачи можно пронумеровать, для этого достаточно множества натуральных чисел, включая ноль. Множество исследуемых объектов, в нашем случае функций, конструируется из конечного числа исходных объектов – базиса – с помощью простых операций, выполнимость которых очевидна.
Простейшие (базисные) функции
К вычислимым функциям можно, очевидно, отнести константы, т.е. все натуральные числа 0, 1, 2,.... Однако нет необходимости
включать в базис бесконечное множества констант. Достаточно задать нуль-функцию и функцию следования.
Нуль-функция – это функция, которая дает значение нуль для любого значения аргумента: 0 x 0 для всех x .
Функция следования f x x 1. Функцию следования часто
обозначают x , т.е. x x 1. Функция следования означает переход к следующему элементу заданного множества и дает возможность получить весь натуральный ряд чисел.
В базис включают ещё третью функцию – функцию тождества, или функцию выделения (выбора) аргумента: Imn x1,x2,...,xn xm для
каждых n 1 и 1 m n .
На основе базисных функций будем строить более сложные вычислимые функции с помощью преобразований, которые назовём операторами.
Операторы
Оператор суперпозиции осуществляет подстановку функций в функции. Это означает, что если функция f функция m
переменных ( m -местная функция), а функции g1, g2,...,gm функции n переменных ( n-местные функции), то оператор суперпозиции Smn
ставит |
в соответствие |
функциям f |
и |
g1, g2,...,gm |
функцию |
h n |
||||||
переменных ( n-местную): |
|
|
|
|
|
|
|
|
||||
Sn |
f ,g ,...,g |
n |
f g x ,...,x ,...,g |
m |
x ,...,x h x ,..., x , |
т.е. |
||||||
m |
1 |
|
1 1 |
n |
|
1 |
n |
1 |
n |
|
||
функция h x1,..., xn есть суперпозиция функций f и g1,...,gm . |
|
|||||||||||
Другой вид оператора, который будем далее использовать, есть |
||||||||||||
оператор примитивной рекурсии. Оператор примитивной рекурсии |
|||||||||||||||
Rn определяет |
n 1 -местную |
функцию |
f |
через |
n -местную |
||||||||||
функцию g и n 2 -местную функцию h следующим образом: |
|
||||||||||||||
|
|
f x1,..., xn ,0 g x1,..., xn ; |
|
|
|
|
|
|
(5.1) |
||||||
|
|
f x ,..., x , y 1 h x ,..., x , y, f x ,..., x |
|
, y . |
|||||||||||
|
|
1 |
|
n |
|
|
|
1 |
n |
1 |
n |
|
|
|
|
Равенство (5.1) называется схемой примитивной рекурсии, а тот |
|||||||||||||||
факт, |
что |
функция |
f |
|
определена |
схемой |
(5.1), |
выражается |
|||||||
равенством |
f x1,..., xn , y Rn g,h . |
|
|
|
|
|
(5.2) |
||||||||
|
|
|
|
|
|
|
|
||||||||
Если |
n 0, |
то |
функция |
f |
|
одноместная, |
|
и |
схема |
(5.1) |
|||||
приобретает вид |
f 0 c; |
f y 1 h y, f y , |
|
|
|
|
(5.3) |
||||||||
|
|
|
|
|
|
|
|||||||||
где c константа. |
|
|
|
|
|
|
|
|
f |
|
|
|
|
||
Отметим, что схемы (5.1), (5.3) определяют |
|
рекурсивно не |
|||||||||||||
только через функции g |
и h , |
но и через значения |
f в предыдущих |
||||||||||||
точках, так как значение |
f |
в точке y 1 зависит от значения f в |
|||||||||||||
точке |
y . |
Для |
вычисления |
f x1,...,xn ,k |
понадобится |
k 1 |
|||||||||
вычислений по схеме (5.1), |
y |
при этом принимает последовательно |
|||||||||||||
значения 0,1, ..., k . Надо иметь в виду, что в операторе примитивной рекурсии независимо от числа переменных в функции f рекурсия ведётся только по переменной y , а остальные n переменных x1, x2,..., xn в схеме (5.1) [(следовательно, и в схеме (5.3)]
зафиксированы и выступают в роли параметров. Схему (5.1) можно записать в развёрнутом виде:
f x1,..., xn |
,0 g x1,..., xn ; |
|
|
|
|
,0 ; |
|
|||||||
f x ,..., x |
n |
,1 h x ,..., x |
n |
,0, f x ,..., x |
n |
|
||||||||
|
1 |
1 |
|
|
|
1 |
|
,1 ; |
|
|||||
f x ,..., x |
n |
,2 h x ,..., x |
n |
,1, |
f x |
,..., x |
n |
(5.4) |
||||||
|
1 |
1 |
|
|
|
1 |
|
|
|
|
||||
................................................................. |
|
|
||||||||||||
|
|
|
, y 1 h x ,..., x |
|
, y, f x ,..., x |
|
, y . |
|||||||
f x ,..., x |
n |
n |
n |
|||||||||||
|
1 |
1 |
|
|
|
|
|
1 |
|
|
|
|||
Нетрудно заметить, что схема примитивной рекурсии образует индуктивный процесс построения функции h , при котором на нулевом шаге используется функция g , а на каждом последующем
шаге – значение функции f от аргументов x1,..., xn , номер y
предыдущего шага и значение функции h , вычисленное на предыдущем шаге. Кроме того, оператор примитивной рекурсии можно применять по любым переменным, входящим в функции f , g
и h (при этом необходимо указать, по какой переменной этот оператор используется).
Функция называется примитивно-рекурсивной, если она может быть получена из базисных функций Ο, x', Imn с помощью конечного
числа применений операторов суперпозиции и примитивной рекурсии.
Этому определению можно придать следующий индуктивный
вид:
1. Функции Ο, x', Imn для всех натуральных n,m, где m n , являются примитивно-рекурсивными.
2. Если g1 x1,..., xn ,..., gm x1,..., xn ,h x1,..., xn примитивно-
рекурсивные функции, то Smn h, g1,..., gm примитивно-рекурсивные
функции для любых натуральных n, m. |
|
|
3. |
Если g x1,..., xn и h x1,..., xn , y, z |
примитивно-рекурсивные |
функции, то Rn g,h примитивно-рекурсивная функция. |
||
4. |
Других примитивно-рекурсивных функций нет. |
|
При м ер . Показать, что функция |
f x, y x y примитивно- |
|
рекурсивна.
Решен и е .
Покажем, что функция f x, y может быть получена из базисных функций и оператора примитивной рекурсии.
|
Учитывая |
|
аналитический |
вид |
функции |
f x, y , |
имеем |
|||||
f x,0 x g x , |
а |
с учетом |
|
|
функции |
тождества получаем |
||||||
f |
x,0 x I1 |
x ; |
с учетом функции следования и заданного вида |
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
f x, y получаем |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x, y 1 f x, y 1 f x, y . |
|
|
||||||
|
Согласно |
(5.1), |
f x, y 1 h x, y, f x, y |
или, |
учитывая |
(5.2), |
||||||
имеем |
|
|
|
f x, y R |
|
I1 x ,h x, y, z , |
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
где h x, y,z f x, y 1 z z 1. |
|
|
|
|
|
|
|
|||||
|
П р и м е р . Показать, что функции |
|
|
|
|
|||||||
а) |
x 1 f x |
и |
б) |
f x, y x |
y |
примитивно-рекурсивны, где |
||||||
функция x y определяется следующим образом:
x y x y, если x y;0, если x y.
Р е ш е н и е .
а) Функция f x одноместная и определяется схемой
f 0 0 1 0; |
|
f y 1 y 1 1 y ; |
|
б) f x, y x y определяется схемой |
|
f x,0 x ; f x, y 1 x y 1 x |
y 1 f x, y 1. |
П р и м е р . Показать, что функция f |
x x! примитивно- |
рекурсивная.
Р е ш е н и е .
По определению, 0! 1. Используем схему (5.4). Пусть g x 1;
h x h x x,
f 0 g 1!; f 1 h f 0 1 1 1 1 1 1 1 2 2!; f 2 h f 1 2 1 2 1 1 2 3 3!;
f 3 h f 2 3 1 2 3 3 1 1 2 3 4 4!;
………………………………………………….,
f x 1 h f x 2 x 1 1 2 3 4 ... x 1 x 1 1
1 2 3 ... x x!.
Всякая примитивно-рекурсивная функция является вычислимой, так как процесс (схема) её определения с помощью примитивнорекурсивного описания дает одновременно и способ вычисления значений функции для любых числовых значений её аргументов.
Машины Тьюринга
Машина Тьюринга полностью определяется:
а) внешним алфавитом А a0 , a1,...,an , причем a0 символ
пустой ячейки, a1 1;
б) алфавитом внутренних состояний Q q0,q1,...,qm , q0 состояние остановки; q1 начальное состояние; в начальном
состоянии машина начинает работать, а попав в состояние остановки, машина прекращает работу;
в) программой, т.е. совокупностью команд, каждая из которых имеет один из следующих видов:
qia j qka ; qia j qka ; qia j qka ,
где 0 k m; 0 n ; 1 i m; 0 j n .
Устройство и работу машины Тьюринга можно представить следующим образом. Машина имеет бесконечную в обе стороны ленту, которая разделена на ячейки. В каждой ячейке записана только одна буква из внешнего алфавита А (запись буквы a0 означает, что
ячейка пуста). Работа машины происходит в дискретном времени. На каждом такте машина находится в одном из состояний, обозначаемых буквами алфавита внутренних состояний, и обозревает единственную ячейку, т. е. считывает информацию, записанную в этой ячейке. Команда qia j qka означает, что машина, находясь состоянии qi и
обозревая ячейку, в которой находится буква a j , переходит в состояние qk , в обозреваемой ячейке стирает букву a j и записывает туда букву a . Команда qia j qka означает, что, находясь в состоянии qi и обозревая ячейку, в которой находится буква a j , машина переходит в состояние qk , в обозреваемой ячейке стирает букву a j и заносит туда букву a , а затем машина переходит к
обозрению ячейки, следующей справа от предыдущей. Команда qia j qka работает, как и предыдущая, с той лишь разницей, что
переход осуществляется к ячейке, следующей слева от предыдущей. После выполнения указанной команды машина на следующем такте переходит к выполнению команды qka qras X , где X или
X , или X отсутствует, и т.д.
Конечная последовательность команд называется программой машины (или функциональной схемой). Функциональную схему (программу) часто задают в виде таблицы. Реализация программы машиной Тьюринга есть выполнение алгоритма, заданного этой программой.
Словом в алфавите А или в алфавите Q , или в алфавите Α Q
называется любая последовательность букв соответствующего алфавита. Под k -й конфигурацией (или машинным словом) будем понимать изображение ленты машины с информацией, сложившейся на ней к началу k -го такта (или слово в алфавите А , записанное на ленте к началу k -го такта) с указанием того, какая ячейка обозревается и в каком состоянии находится машина. Каждая конфигурация конечна, т.е. все ячейки ленты, за исключением конечного числа их, пусты.
Непустое слово w в алфавите А a1,...,an воспринимается
машиной в стандартном положении, если это слово записано в последовательных ячейках ленты, все другие ячейки пусты и машина обозревает крайнюю справа ячейку из тех, в которых записано слово w . Стандартное положение называется начальным (заключительным), если машина, воспринимающая слово в стандартном положении, находится в состоянии q1 (в состоянии q0
соответственно). Будем говорить, что слово w перерабатывается машиной в слово v , если от слова w , находясь в начальном стандартном положении, машина после выполнения конечного числа команд приходит к слову v , воспринимаемому машиной в заключительном стандартном положении.
Пусть на множестве слов алфавита a1,...,a определена k -
местная функция, областью значений которой является множество слов в этом же алфавите. И пусть машина Тьюринга с алфавитом А a0 , a1,..., an n любой набор, состоящий из k слов из области
определения функции (набор этих слов записан на ленту с промежутками между словами в одну ячейку), перерабатывает в слово, являющееся значением функции для этого набора, а для набора из k слов, не входящего в область определения функции, машина работает бесконечно. Тогда говорят, что машина Тьюринга
вычисляет данную функцию, а функция называется вычислимой (по Тьюрингу).
Рассмотрим применение машин Тьюринга к словам.
