
1798
.pdf161 |
|
Высота ножки hf зуба принята равной |
|
hf = 1,25 m. |
(16.6) |
Полная высота зуба h будет равна сумме высот головки и ножки |
|
h = hа + hf = m+ 1,25 m = 2,25 m . |
(16.7) |
Диаметр начальной окружности определяется из формулы (16.4) |
|
d = m z . |
(16.8) |
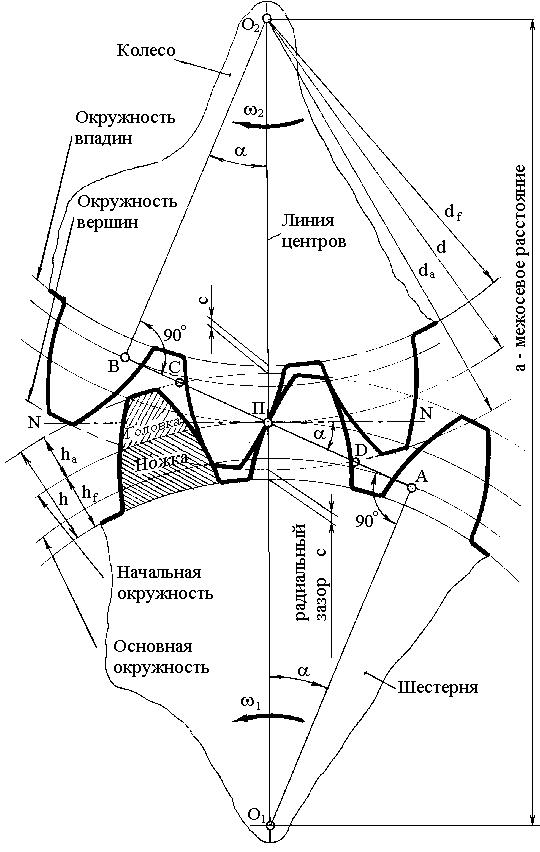
Окружность, которая описывает вершины головок |
зубьев, |
называется окружностью вершин. Ее диаметр складывается из диаметра начальной окружности, к которому с каждой стороны прибавлено по высоте головки зуба, т. е
da = d + 2ha = mz + 2m = m (z+2). |
(16.9) |
Окружность, которая описывает впадины зубьев, |
называется |
окружностью впадин. Ее диаметр является разностью между диаметром делительной окружности и двумя высотами ножек зубьев (с каждой стороны по одной ножке), т. е.
df = d – 2 hf = m z – 2 x1,25 m = m (z – 2,5). |
(16.10) |
Для того чтобы вершина головки зуба одного колеса не задевала донышко, впадины между зубьями другого колеса, между вершиной и впадиной делают зазор c (рис. 16.3).
Нужно, чтобы впадина была глубже вершины зуба. Вот для этого высоту ножки зуба делают больше, чем головки.
Из чертежа (см. рис. 16.3) видно, что величина зазора c является
разностью между высотами ножки и головки зуба, т. е. |
|
c = hf – ha = 1,25m – m = 0,25 m . |
(16.11) |
Межосевое расстояние двух сопряженных зубчатых колес (см. рис. 16.1 и 16.3) складывается из двух радиусов начальных окружностей О1П = r1 =
d1/ 2 и O2П = r2 = d2 /2: |
|
d1 |
|
d2 |
|
mz1 |
|
mz2 |
|
z1 z2 |
|
|
|||
a r |
r |
|
|
|
|
m |
. |
(16.12) |
|||||||
|
|
|
|
|
|||||||||||
1 |
2 |
2 |
2 |
2 |
|
|
2 |
2 |
|
|
|||||
Ширина зубчатого колеса b (см. рис. 16.2) определяется по формуле |
|||||||||||||||
|
|
|
|
|
|
b = · m , |
|
|
|
|
(16.13) |
||||
где – коэффициент ширины зуба.
Боковые поверхности зубьев очерчены кривыми, которые называются «эвольвента» (см. рис. 16.13), поэтому изучаемый нами вид зацепления называется эвольвентным.
При вращении зубчатых колес зуб шестерни перекатывается по зубу колеса. Точка касания зубьев при вращении колес движется по прямой АВ, которая называется общей нормалью. Зуб шестерни встречается с зубом колеса в точке D, далее перекатывается по зубу колеса таким образом, что точка касания (контакта) зубьев движется по прямой АВ, затем в точке С зуб шестерни расцепляется с зубом колеса. Отрезок СD называют длиной зацепления, а отрезок АВ – линией зацепления.
162
Если провести линию NN через точку П перпендикулярно к линии центров О1О2, то линия NN будет касательной к начальным окружностям зубчатых колес. Угол , образованный касательной NN и линией зацепления АВ, называют углом зацепления. Его значение согласно стандарту = 200.
Опустим перпендикуляры из центров О1 и О2 на общую нормаль АВ. Окружности, описанные радиусами О1А и О2В, называют основными. Скорость точки А находим по формуле
v = 1 АО1 . |
(16.14) |
При вращении колес линия АВ остается перпендикулярной к О1А, следовательно, скорость точки вдоль линии АВ будет определяться формулой (16.14), т. е. будет величиной постоянной. Скорость точки В,
определенная через параметры колеса, |
|
v = 2 О2В . |
(16.15) |
Так как скорость в точке А равна скорости в точке В, уравнение (16.14) и (16.15) можно приравнять.
|
|
v = 1 |
О1А = 2 О2В = const |
(16.16) |
|||||||||||||||||||||
или с учетом формулы (16.2) |
|
O2B |
|
|
|
|
|
||||||||||||||||||
|
|
u |
|
|
|
|
|
1 |
|
|
const . |
(16.17) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
12 |
|
|
|
|
2 |
|
|
|
|
O A |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
Из подобия треугольников О1 АП и О2ВП находим |
|
||||||||||||||||||||||||
|
O2B |
|
O2п |
|
|
d2 |
|
|
2 |
|
d2 |
. |
(16.18) |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
O1A O1п |
|
|
|
|
|
2 d1 |
|
|
|
d1 |
|
|||||||||||||
Из формулы (16.8) мы можем получить |
|
||||||||||||||||||||||||
|
|
d1 = mz1; d2 = mz2 . |
(16.19) |
||||||||||||||||||||||
Решив совместно уравнения (16.2, 16.18 и 16.19), получим |
|
||||||||||||||||||||||||
|
u |
|
1 |
|
|
d2 |
|
|
z2 |
. |
(16.20) |
||||||||||||||
|
|
|
d |
|
|
||||||||||||||||||||
12 |
|
|
2 |
|
|
|
|
|
|
|
z |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
||||||
Из вышесказанного следует важный вывод: передаточное отношение зубчатой передачи есть величина постоянная.
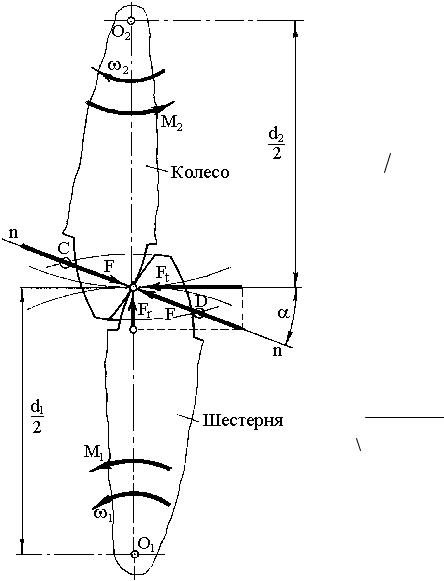
Шестерня (рис. 16.4) приводится в движение моментом М1. Зуб шестерни толкает зуб колеса и, преодолевая момент сопротивления М2, вращает колесо. Силы взаимодействия F согласно законам статики направлены «перпендикулярно» к поверхностям в точке касания, а точнее по нормали n-n, которая называется общей нормалью.
163
Рис.16.3
164 |
|
|
Разложим |
силу |
F для |
удобства расчетов |
на |
две |
составляющие: окружную, или тангенциальную силу Ft, и радиальную Fr .
Окружную силу можно определить через момент и диаметр по формуле
(16.21)
где М – крутящий момент на зубчатом колесе; d – диаметр начальной окружности или начальный диаметр.
Радиальную силу определяют
через окружную. |
|
Fr = Ft tg . |
(16.22) |
Силу нормального давления между зубьями находят либо по теореме Пифагора, либо через окружную силу
F 
 Ft2 Fp2 ;F=Ft / cos ,(16.23)
Ft2 Fp2 ;F=Ft / cos ,(16.23)
где – угол зацепления.
Момент М1 = Ft d1/2 является движущим моментом, а момент
М2 = Ft d2/2 является моментом сопро-тивления.
Рис.16.4
В точке С сила F приложена к вершине зуба шестерни, а в точке D сила F приложена к вершине зуба колеса.
16.2. Расчет зубьев цилиндрических колес
Для изготовления зубчатых колес принимают, главным образом, конструкционную сталь. Шестерня имеет меньшее число зубьев, вращается быстрее, каждый ее зуб чаще входит в зацепление, поэтому интенсивнее изнашивается. Чтобы выровнять долговечность шестерни и колеса, шестерню делают тверже, чем колесо, примерно в 1,25 раза. Есть вторая причина. В начальный период работы зубчатого зацепления зубья должны притираться (прирабатываться) друг к другу, чтобы получился правильный эвольвентный профиль зубьев. Для этого шестерню делают
165
тверже, точнее и шире, чем колесо. Шестерня как более твердая является притиром для зубьев колеса. Изнашивается и притирается колесо, а шестерня не изменяет ни форму, ни размеры. Поэтому шестерня должна изготавливаться точнее. Чтобы зуб колеса равномерно притирался по всей ширине, зуб шестерни должен быть шире колеса.
Для повышения долговечности зубчатые колеса делают тверже «сырых» сталей. Для этого применяют метод термической обработки. Зубчатое колесо нагревают до высокой температуры, а затем быстро охлаждают в воде или масле. Этот метод называют закалкой. Закалка повышает не только твердость, но и прочность стали.
По твердости зубьев стальные колеса делят на две группы: с твердостью НВ 350 и с твердостью НВ 350.
Зубчатые колеса первой группы вначале начерно изготавливают и закаливают до твердости НВ 350. Затем производят чистовое нарезание зубьев, т. к. такая твердость позволяет это делать фрезами, резцами, долбяками. Зубчатые колеса хорошо прирабатываются и имеют достаточную вязкость, чтобы хорошо сопротивляться изгибу и излому от ударной нагрузки.
Зубчатые колеса второй группы имеют другую технологию изготовления. Подавляющее большинство зубчатых передач в настоящее время делают закрытыми, помещенными в специальный корпус. Внутри корпуса обеспечивается хорошая смазка и туда не попадает пыль и другие виды загрязнений, частицы которых твердые и, попадая между зубьями, царапают и изнашивают их.
Критерием работоспособности и долговечности закрытых передач является контактная прочность зубьев, для повышения которой применяется закалка до твердости НВ 350. Такая твердость зубьев не позволяет нарезать их после закалки, поэтому нарезание зубьев делают до закалки, а после их шлифуют до высокой точности. Вместо приработки, исправляющей форму зубьев, применяют шлифовку. Этот метод дорогой, но он используется для повышения нагрузочной способности передачи, уменьшения ее габаритов и повышения долговечности.
Рис.16.5
166
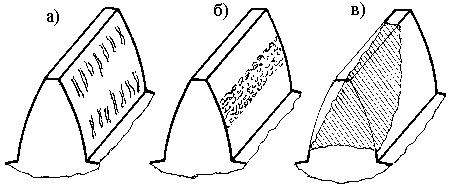
Зубчатые колеса повреждаются, главным образом, по трем причинам: абразивным износом боковых поверхностей зубьев (рис. 16.5, а), усталостным выкрашиванием боковых поверхностей зубьев (рис. 16.5, б) и поломкой зубьев (рис. 16.5, в).
Абразивный износ возникает в открытых передачах, где на зубья оседает пыль и другие абразивные частицы. Когда они попадают между зубьями, то царапают боковые поверхности, постепенно изнашивая их. Износ боковых поверхностей уменьшает толщину зуба и нарушает зацепление зубьев, их эвольвентный профиль. Чем зуб тоньше, тем напряжения от изгиба в нем больше. Возрастание напряжений ведет к поломке зубьев.
В закрытых зубчатых передачах при обильной смазке наблюдается усталостное выкрашивание рабочих поверхностей зубьев. Суть его заключается в следующем. Каждый зуб за один оборот встречается с зубом сопряженного колеса. Зубья давят друг на друга, а затем расстаются до следующей встречи. Вот эти надавливания напоминают удары молотка, в результате которых поверхностный слой зубьев уплотняется, а затем начинает растрескиваться. Образуются отдельные чешуйки, которые потом отслаиваются и выкрашиваются. На их месте образуются язвочки, которые в дальнейшем разрастаются, как оспа. Боковая поверхность зуба выходит из строя.
Периодическое нагружение и разгружение зубьев приводят к тому, что у корня зуба возникают растягивающие и сжимающие переменные напряжения изгиба, которые с течением времени приводят к появлению трещин, а затем и к поломке зуба. Этим видом разрушения пользуются в быту, когда нужно отломить кусок стального провода. Его начинают перегибать взад – вперед до появления сначала трещин, а потом и поломки. Такой вид разрушения присущ и открытым и закрытым передачам.
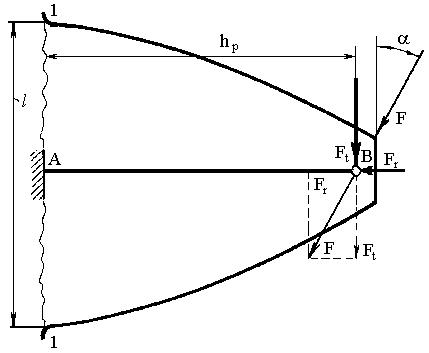
Расчет зубьев на изгиб предназначен для определения модуля зубчатого зацепления. При расчете (рис. 16.6) зуб рассматривают как консольную балку АВ равного сопроти-вления, силу F прикладывают к вершине зуба шестерни в точке С (см. рис. 16.4). Вершина зуба наиболее удалена от основания, и изгибающий момент от силы F получается наибольший. Опасным принимают сечение 1-1 у корня зуба. Силу F переносим по линии ее действия в точку В, а затем раскладываем на две составляющие Ft и Fr [см. формулы (16.21); (16.22) и (16.23)].
Окружная сила Ft изгибает зуб, а радиальная сила Fr сжимает его. Наибольший изгибающий момент
Мu = Ft · hp , (16.24)
где hp – расчетная длина консоли или плечо силы Ft относительно сечения
1-1.
167
Сечение 1-1 имеет прямоугольную форму. Ширина зубчатого колеса (длина зуба) b = m
(см. рис. 16.2 и формулу (16.13)).
Толщину зуба у основания обозначим буквой l.
Величины hp и l пропорциональны модулю: hp = km; l = qm, где k и q –
коэффициенты, зависящие от формы зуба, от угла и числа зубьев z.
Осевой момент сопротивления в сечении 1-1
Рис.16.6 |
|
|
|
|
Wx |
b l |
2 |
. |
(16.25) |
|
|
|||
6 |
|
|
|
|
Если пренебречь напряжениями от сжатия, которые сравнительно малы по отношению к напряжениям от изгиба, то условие прочности зуба на изгиб имеет вид
|
|
|
|
Mu |
|
[ u |
]. |
|
|
(16.26) |
|||||
|
|
|
Wx |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Предельный момент из формулы (16.26) |
|
|
|
|
|
|
|
|
|||||||
|
|
|
Mu Ft hp Wx[ u]. |
(16.27) |
|||||||||||
Подставив в формулу (16.27) значения hp; Wх; в и l, получим |
|
||||||||||||||
|
|
|
F km |
bq2m2 |
[ |
u |
], |
|
|||||||
|
|
|
|
|
|||||||||||
|
|
|
t |
|
|
|
|
6 |
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
bmq2 |
|
|
|
|
|
|
|
|||||
|
|
|
F |
[ |
u |
], |
|
|
|
||||||
|
|
|
|
|
|
||||||||||
|
|
|
t |
|
6k |
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
|||||
где |
q |
y называется коэффициентом формы зуба и определяется |
|||||||||||||
|
|
||||||||||||||
|
6k |
|
|
|
|
|
|
|
|
|
|
|
|
||
по табл. 16.1. С учетом этого
168
|
|
|
|
Ft bmy[ u]. |
|
|
(16.28) |
|||
|
|
Значение коэффициента У при угле = 200 |
Таблица 16.1 |
|||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Число |
|
|
|
|
|
|
|
|
|
|
зубьев |
10 |
12 |
14 |
|
15 |
16 |
18 |
20 |
|
25 |
У |
0,292 |
0,304 |
0,324 |
|
0,332 |
0,339 |
0,354 |
0,372 |
|
0,398 |
|
|
|
|
|
|
|
|
|
|
|
Число |
|
|
|
|
|
|
|
|
|
|
зубьев |
30 |
34 |
40 |
|
50 |
80 |
100 |
300 |
|
Рейка |
У |
0,416 |
0,428 |
0,442 |
|
0,457 |
0,478 |
0,481 |
0,496 |
|
0,523 |
По формуле (16.28) можно проверять допускаемую величину окружной силы.
Для проектировочного расчета необходимо определить главный параметр зубчатого зацепления – модуль. Подставив в формулу (16.28) значение длины зуба b [см. формулу (16.13)], силы Ft из формулы (16.21), начального диаметра d из формулы (16.8), получим
F |
2M |
|
2M |
m m y[ |
u |
] y m2 |
[ |
u |
]. |
|
|
||||||||
t |
d mz |
|
|
|
|||||
Решив это уравнение относительно крутящего момента, получим
2M y m3z[ u].
По формуле (16.29)можно проверять допускаемый крутящий момент.
Формулу (16.29) можно переписать в виде ( m = b)
2M
yzbm2 [ u].
(16.29)
(16.30)
По формуле (16.29) делают проверочный расчет зубьев на изгиб. Если формулу (16.29) решить относительно модуля m, то получим
m 3 |
2M |
. |
(16.31) |
|
 yz [ u]
yz [ u]
По данной формуле проводится проектировочный расчет модуля цилиндрической зубчатой передачи.
При расчете зубьев на прочность нужно учитывать динамический характер приложения нагрузки F и возможный перекос зубьев. Поэтому рассчитанный по формулам
M |
1 |
9,55 |
N1 |
; |
M |
1 |
|
N1 |
; |
M |
2 |
M |
1 |
u |
|
и т. д. крутящий |
|
|
|||||||||||||||||
|
|
||||||||||||||||
|
|
|
n |
|
|
|
|
|
12 |
12 |
|
||||||
момент М1 |
1 |
|
|
|
1 |
|
|
|
|
|
|
нагрузки k = 1,3 при |
|||||
нужно |
умножать на |
коэффициент |
|||||||||||||||
169
симметричном относительно опор расположении зубчатого колеса и k = 1,5 – при несимметричном. Обычно рассчитывают шестерню, тогда окончательно
m 3 |
2M1 k |
, |
(16.32) |
|
 yz1 [ u]
yz1 [ u]
где m – модуль, мм; М1 – крутящий момент на шестерне, Н·мм; У – коэффициент формы зуба; z – число зубьев шестерни; = 10-20 – коэффициент ширины зуба; k – коэффициент нагрузки; [ u] – допускаемое напряжение при изгибе, Н/мм2.
Допускаемые напряжения при изгибе определяются по формуле
[ u] |
np |
9 |
|
N0 |
|
, |
(16.33) |
S |
|
N |
|||||
|
|
|
|
|
|
где пр – предельное напряжение, МПа; S – коэффициент запаса прочности; N0 – базовое число циклов нагружения, для стали N0 = 4 106; N – заданное число циклов нагружения зуба; 9 – показатель степени корня.
Для нормализованных конструкционных углеродистых сталей при НВ 180… 350 предельное напряжение пр = 1,8 НВ, а коэффициент S = 1,75. Подставив эти данные в формулу (16.33), получим
u |
|
1,8НВ |
|
4 106 |
|
4 106 |
|
|
9 |
|
НВ |
|
. |
||
1,75 |
|
N |
|
||||
|
|
|
|
N |
|||
По этой формуле можно определить допускаемое напряжение для конструкционных углеродистых сталей с НВ 350.
Зачастую выбирают стали твердостью НВ = 280 для шестерни и НВ = 250 для колеса. Выбирая меньшее значение, получим при неограниченном сроке службы
и |
НВ 9 |
4 106 |
|
250 1 250МПа . |
||||
N |
||||||||
|
|
|
|
|
|
|||
В приближенных расчетах можно принимать для конструкционных |
||||||||
сталей с НВ 350 значение корня |
9 |
|
1, |
а формулу (16.33) |
||||
N0 / N |
||||||||
переписать в виде |
|
[ u] НВ . |
(16.34) |
|||||
|
|
|||||||
Расчет зубьев на |
контактную |
|
прочность |
предназначен для |
||||
закрытых зубчатых передач, которые работают с обильной смазкой. В них процесс выкрашивания протекает гораздо интенсивнее, чем процесс истирания (изнашивания) зубьев, который характерен для открытых передач.
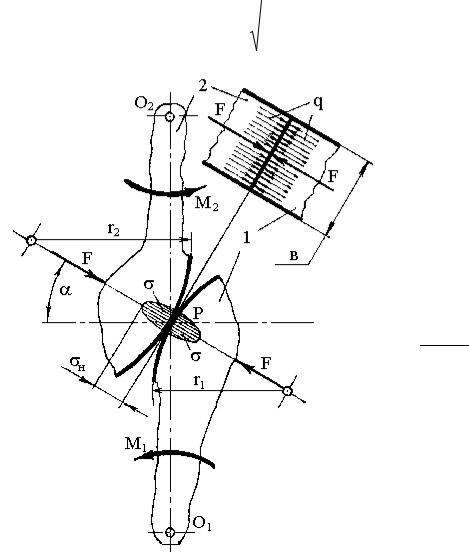
На рис. 16.7 показаны два зубчатых колеса: 1 – шестерня и 2 – колесо. Их зубья находятся в контакте и прижимаются друг к другу силами F, которые возникают под действием моментов М1 и М2. Зубья
170
представляют собой два цилиндра с радиусами r1 и r2 и длиной b. Силы F равномерно распределяются по длине, в результате получается равномерно распределенная нагрузка q.
q = F/b |
(16.35) |
На контактирующей поверхности каждого зуба возникают контактные напряжения сжатия , которые в центре контакта на полюсе P максимальные и равны н, удаляясь от центра контакта они убывают, а на краю контакта равны нулю. В районе полюса в первую очередь наблюдается усталостное выкрашивание, поэтому расчет на контактную прочность ведут для этого положения.
Расчет заключается в определении наибольших контактных напряжений н и сопоставлении их с допускаемыми [ н].
Наибольшее контактное напряжение определяется по формуле
Герца: |
|
|
|
|
|
|
|
|
|
Н |
E |
|
q |
, |
(16.36) |
||||
2 (1 2) |
|
||||||||
|
|
|
r |
|
|
|
|||
|
|
|
|
|
|
где |
E |
2E1 E2 |
– |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
E1 E2 |
|
приведенный модуль упругости; Е1 и Е2 – модули упругости шестерни и колеса соответственно; если оба колеса стальные, то Е = Е1= Е2; q – равномерно распределенная или погонная нагрузка на единицу длины зуба;
r r1 r2 – приведенный r1 r2
радиус кривизны профилей зубьев; r1, r2 – радиусы кривизны зубьев шестерни и колеса соответственно; – коэффициент поперечного сжатия, или коэффициент Пуассона. Еcли коэффициент Пуассона в среднем
Рис.16.7
