
1798
.pdf
111
10.2.Расчет валов на прочность и жесткость
Впредыдущем параграфе было показано, что наибольшие касательные напряжения располагаются на поверхности вала. Они являются опасными напряжениями и не должны превосходить допускаемых, т.е.
max |
Mk |
k . |
(10.18) |
|
Wp |
||||
|
|
|
Это уравнение является условием прочности при кручении.
С помощью формулы (10.18) можно проводить три вида расчетов, аналогичных деформации растяжения (см. § 8.2).
1.Проверочный расчет проводится по формуле (10.18), чтобы убедиться в прочности детали после того, как узел спроектирован.
2.Проектный расчет. Для этого уравнение (10.18) нужно решить относительно Wр:
Wp |
Mk |
|
k . |
(10.19) |
Момент инерции для круглого сечения определяется по формуле
Ip |
d4 |
|
||
|
, |
(10.20) |
||
32 |
||||
|
|
|
||
где d – диаметр вала.
Момент сопротивления для круглого сечения определяется по формуле
Wp |
d3 |
|
||
|
. |
(10.21) |
||
16 |
||||
|
|
|
||
Подставив значение Wр в формулу (10.19) и решив ее относительно диаметра d, получим
16Mk |
|
|
d 3 |
. |
(10.22) |
k |
||
Проектный расчет предусматривает определение диаметра вала по известным крутящему моменту Мк и допускаемому напряжению [ к].
3. Расчет предельного момента проводят с целью определения наибольшей нагрузки на вал по формуле, полученной из формулы (10.18),
Мпр = [ k] Wp . |
(10.23) |
Два вала разных диаметров и изготовленных из разных материалов |
|
называются равнопрочными, если |
|
Мпр1 = Мпр2 |
(10.24) |
или |
|

112
[ k1] Wp1 = [ k2] Wp2 . |
(10.25) |
Это уравнение называется условием равнопрочности.
Соблюдение условия прочности (10.18) часто бывает недостаточным. Длинные валы при допускаемом крутящем моменте, т.е. при обеспеченной прочности, закручиваются на большой угол, а если момент Мк не постоянен, то они "играют", как пружина, вызывая колебания (вибрации). Это очень вредно для работы машины. Поэтому установлены допускаемые значения угла закрутки, точнее относительного угла закрутки , определяемого по формуле (10.1) и являющегося характеристикой жесткости вала.
Требование достаточной жесткости вала определяется по условию
|
|
|
Mk |
, |
(10.26) |
|
|
||||
|
l |
GIp |
|
||
где допускаемый относительный угол закрутки вала
[ ] = (0,25 ... 1) град/м = (0,0045 ... 0,0175) рад/м . (10.27)
Проверочный расчет на жесткость проводят по формуле (10.26). Проектный расчет на жесткость – по формуле
d 4 |
32Mk |
|
|
|
. |
(10.28) |
|
G |
|||
Предельный момент по жесткости рассчитывают по формуле |
|
||
Мпр = GJр [ ]. |
(10.29) |
||
Произведение GJр называется жесткостью сечения вала при кручении. Аналогом при растяжении является произведение ES (см. § 8.3).
Жесткостью вала при кручении называется отношение крутящего
момента к углу закручивания, т.е. |
M |
|
|
GIp |
|
|
jk |
k |
|
. |
(10.30) |
||
|
|
l |
||||
|
|
|
|
|||
Это выражение получено из формулы (10.17). Валы разных размеров и изготовленные из разных материалов имеют равную жесткость, если
|
|
Mk1 |
|
|
|
Mk2 |
|
|
(10.31) |
|
|
1 |
|
2 |
|||||
|
|
|
|
|
|
||||
или |
|
|
|
|
|
|
|
||
|
G1Ip1 |
|
G2Ip2 |
, |
(10.32) |
||||
|
|
|
|||||||
|
|
l1 |
|
|
|
l2 |
|
||
где параметры, имеющие индекс 1, относятся к первому валу, а индекс 2 – ко второму.
113
10.3.Полярные моменты инерции и сопротивления
В§ 10.1 полярным моментом инерции был назван интеграл
|
|
|
2dS Ip |
(10.33) |
|
|
|
|
s |
|
|
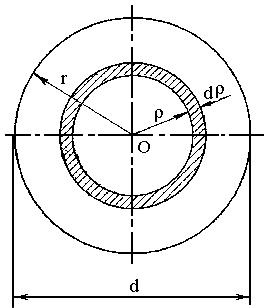
Рассмотрим круг радиусом r, в котором |
|
||||
все элементарные площадки dS, |
|
||||
удаленные от центра O (рис.10.1, б) на |
|
||||
расстояние |
, |
объединены |
в |
|
|
элементарное |
кольцо шириной |
d |
|
||
(рис.10.3). |
|
|
|
|
|
Элементарная площадь этого кольца |
|
||||
равна площади |
прямой |
полосы |
|
||
шириной d и длиной 2 , т.е. |
|
|
|
||
dS = 2 d . |
|
|
(10.34) |
|
|
Подставив значение dS в формулу |
|
||||
(10.33), получим |
|
|
|
|
|
r |
|
r |
|
|
|
Jp 22 d 2 3d . |
(10.35) |
|
|||
0 |
|
0 |
|
|
|
Рис.10.3
Интегрирование проводят в пределах изменения текущего радиуса от 0 до r. После интегрирования имеем
Jp |
r |
4 |
|
d4 |
|
|
|
|
|
. |
(10.36) |
||
|
|
32 |
||||
2 |
|
|
|
|
||
Мы получили формулу (10.36), где d – диаметр круга. Из уравнения (10.14) явствует, что полярный момент сопротивления
Wp |
Jp |
|
r4 |
|
r |
3 |
|
d3 |
|
|
|
|
|
|
|
. |
(10.37) |
||||
r |
2r |
|
|
16 |
||||||
|
|
2 |
|
|
|
|
||||
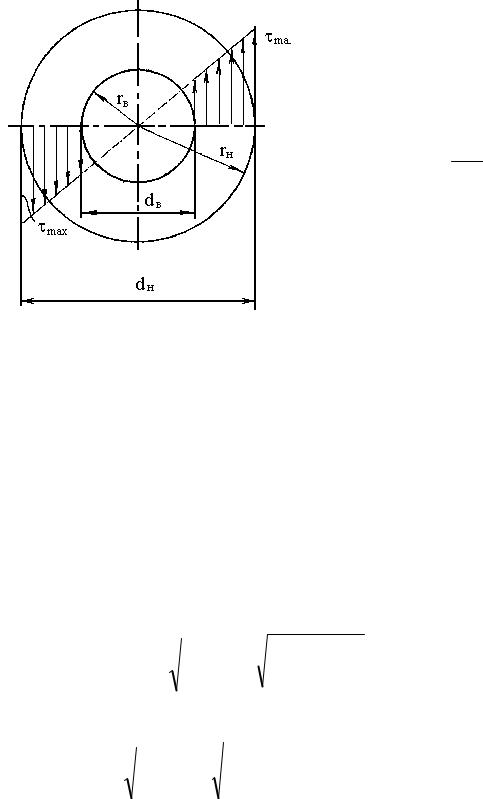
В § 10.1 отмечалось, что напряжения в сечении вала согласно формуле (10.10) и рис. 10.1, б распределяются прямо пропорционально радиусу и сердцевина вала слабо нагружена. Для уменьшения массы вала его делают полым, удаляя внутреннюю часть и получая кольцевое сечение
(рис. 10.4).
Момент инерции для кольцевого сечения рассчитывается по формуле (10.35), в которой изменяются пределы интегрирования
rh |
|
Jp 2 3d . |
(10.38) |
rв
|
114 |
|
|
|
|
|
|
|
|
|
r4 |
r4 |
|
|
|||
После интегрирования получим |
Jp |
h |
|
в |
|
|
(dн4 dв4). |
(10.39) |
2 |
2 |
|
||||||
|
|
|
|
32 |
|
|||
|
|
|
|
Если |
обозначить |
отношение |
||
|
диаметров |
|
|
|
||||
dв 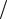 dн
dн
(10.40)
и подставить в формулу (10.39), то получим
Jp dн4 (1 4).
32
(10.41)
Если уравнение (10.41) разделить на rн = dн/2, то получим
Wp |
dн3 |
(1 |
4 |
). |
(10.42) |
|
|
||||
16 |
|
|
|
|
|
Рис.10.4
10.4. Примеры расчетов
Пример 1. Стальной вал сплошного сечения передает мощность N = 60 кВт. Частота вращения вала n = 240 об/мин. Определить диаметр вала d из условий прочности и жесткости, если [ k] = 40 МПа, допускаемый угол закручивания [ 0] = 1 град/м, модуль сдвига G = 8·105 МПа.
Р е ш е н и е.
Определяем крутящий момент, приложенный к валу,
Mk |
9,55 |
N |
9,55 |
60000 |
2387Нм = 2,4·106Н·мм. |
n |
|
||||
|
|
240 |
|
||
Из расчета на прочность по формуле (10.22) определяем диаметр
вала
|
|
|
|
16М |
к |
|
|
|
|
|
16 2,4 106 |
|||||||||||||||
|
|
d 3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
67,3мм . |
|||||||||
|
|
|
|
к |
|
|
|
40 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Определяем диаметр вала из расчета на жесткость по формуле |
||||||||||||||||||||||||||
(10.28) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 2,4 106 |
|
|
|
|
|||||||
d |
4 |
|
32Мк |
|
4 |
|
|
|
|
|
|
|
|
|
36,3мм , |
|||||||||||
|
G |
|
|
|
|
|
|
10 |
5 |
1,75 |
|
10 |
5 |
|
||||||||||||
где 0 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1,75 10 5рад/мм. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
180 1000 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
180 1000 |
|
|
|
|
|
|
||||||||||||||||
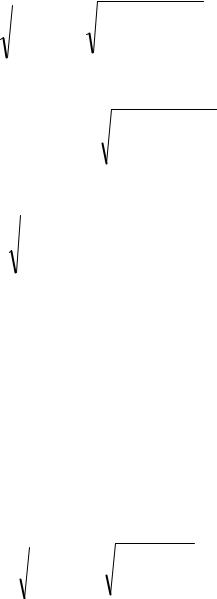
115
Выбираем диаметр вала из расчета на прочность d = 70 мм. Пример 2. От сплошного вала к полому через кулачковую муфту
передается мощность N = 10 кВТ при частоте вращения n = 100 об/мин. Подобрать диаметр d сплошного вала и наружный диаметр dн полого вала при коэффициенте полости = 0,7, приняв допускаемое касательное напряжение [ k] = 60 МПа.
Р е ш е н и е Определяем крутящий момент, передаваемый валами,
Mk |
9,55 |
N |
9,55 |
10000 |
955Нм = 0,95·106Н·мм. |
n |
|
||||
|
|
100 |
|
||
Подбираем диаметр сплошного вала по формуле (10.22)
|
16М |
к |
|
|
16 0,95 106 |
|
||
d 3 |
|
|
3 |
|
43 |
мм. |
||
к |
|
|
||||||
|
|
|
|
60 |
|
|||
Для полого вала в формулу (10.19) подставляем значение Wр из формулы (10.42) и решаем в отношении диаметра dн, получаем
|
|
|
d’ 3 |
|
|
16Мк |
|
|
|
|
|
|
|
|
. |
(10.41) |
|
|
(1 4) к |
|||||||
В формулу (10.42) подставляем числовые значения и находим |
||||||||
диаметр полого вала |
|
|
|
|
|
|||
|
|
|
|
|
|
|||
dн |
3 |
16 0,95 106 |
47мм. |
|
||||
|
|
|
|
|||||
|
|
|
(1 0,74)60 |
|
||||
Расчет показывает, что диаметр полого вала всего лишь на 10 % больше сплошного.
Пример 3. Сравнить массы и углы закручивания двух сплошных круглых валов длиной l = 2 м каждый, воспринимающих одинаковые крутящие моменты Мк = 1кНм. Один вал стальной, другой из алюминиевого сплава. Диаметры валов подобрать по условию прочности. Дано: для стального вала [ k] = 80 МПа, = 7,85·103кг/м3, G = 8·104МПа, для вала из алюминиевого сплава [ k] = 50 МПа, = 2,6·103кг/м3, G = 3 104МПа.
Р е ш е н и е
Подбираем диаметр валов из условия прочности: для стального вала
dст |
|
16М |
к |
|
|
16 1 106 |
|
||
3 |
|
|
3 |
|
40 |
мм; |
|||
к |
|
|
|||||||
|
|
|
|
|
80 |
|
|||
для алюминиевого вала

|
|
|
|
|
|
116 |
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
16 1 106 |
|
|
||
|
16М |
к |
|
|
|
|||||
d 3 |
|
|
3 |
|
|
|
46,7 |
мм. |
||
к |
|
|
||||||||
|
|
|
|
|
50 |
|
||||
Определяем полярные моменты инерции: для стального вала
J р.ст d4 404 2,5 105 мм4; 32 32
для алюминиевого вала
|
J |
р.ал |
|
d4 |
|
46,74 |
|
4,7 105 |
мм4. |
||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
32 |
|
|
|
|
32 |
|
|
|
|
|
|||||||
Отношение углов закручивания (см. формулу (10.17)) |
|||||||||||||||||||||||
|
ал |
|
GстIр.ст |
1,43. |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
ст |
|
GалIр.ал |
|
|
|
|
|
|
|
|
||||||||||||
Масса вала определяется по формуле |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
V |
|
|
|
l, |
|
(10.42) |
|||||
а отношение масс |
|
4 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
d2 |
|
|
|
|
|
7,85 103 402 |
|
|
||||||||||||||
|
m |
ал |
|
|
|
ст |
р.ст |
|
|
|
2,2. |
||||||||||||
|
mст |
алd2 |
р.ал |
|
2,6 103 46,72 |
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
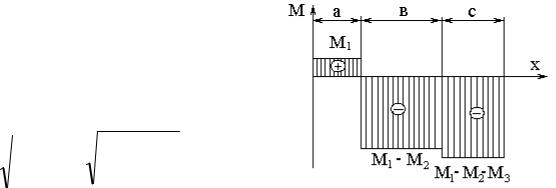
Пример 4. Подобрать диаметр вала, нагруженного моментами М1=2 кН·м; М2=10 кН·м; М3=1 кН·м; М4=9 кН·м. Допускаемое касательное напряжение для материала вала [ k] = 50 МПа. Построить эпюры крутящих
моментов.
Р е ш е н и е
Если смотреть на торец вала, то момент, вращающий вал против часовой стрелки, будет
Рис.10.5
положительным, а по часовой стрелке – отрицательным. Будем смотреть на вал с торца А. На участке длиной a будет действовать крутящий момент М1 = 2 кН·м, он будет положительным. На участке длиной b будет действовать два момента: положительный М1 и отрицательный М2=10 кН·м. Их алгебраическая сумма будет равна 8 кН·м. На участке длиной c будет действовать три момента: + М1; - М2 и М3=-1кНм. Их алгебраическая сумма равна - 9к Н·м. Перенесем все на график (эпюру) рис. 10.6.
117
Если начинать суммирования с торца B, то на участке c будет действовать крутящий момент (см. на торец B), который вращает вал по часовой стрелке, значит, он имеет отрицательный знак, т.е. М4 = -9 кН·м, что соответствует эпюре, изображенной на рис.10.6.
Итак, согласно эпюре наибольший крутящий момент будет на участке длиной c. По наибольшему моменту подберем диаметр вала из условия прочности
|
16М |
к |
|
|
16 9 106 |
|
||
d 3 |
|
|
3 |
|
97 |
мм. |
||
к |
|
|
||||||
|
|
|
|
50 |
|
|||
Рис.10.6
11.ИЗГИБ
11.1.Основные понятия
Изгибу подвергаются длинные детали типа стержней, у которых поперечные размеры малы по сравнению с длиной (балки, валы и др.). Изгиб появляется под действием поперечных внешних сил и реакций опор, вызывающих изгибающие моменты. Такой изгиб называют поперечным. Если на стержень действуют только продольные силы, под действием которых стержень теряет устойчивость и прогибается, то такой изгиб называют продольным.
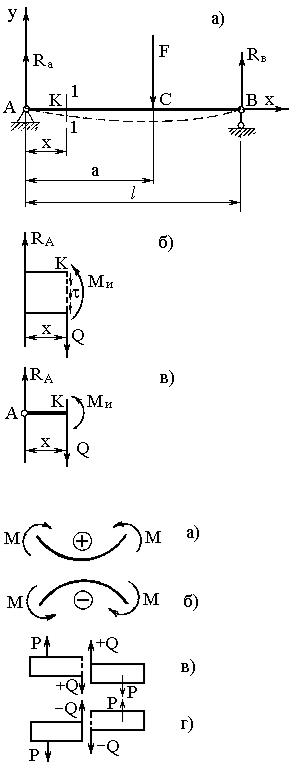
Рассмотрим балку на двух опорах (рис.11.1), нагруженную силой F. В опорах А и В на балку будут действовать реакции опор RА и RВ. Под действием силы F и реакций опор балка будет прогибаться, что отмечено пунктирной линией.
Мысленно рассечем балку сечением 1-1 в произвольной точке Ê на расстоянии х от начала координат (точки А).
Теперь отбросим опоры и правую часть балки КСВ и рассмотрим равновесие оставшейся части АК(рис.11.1,б). Чтобы оставшаяся часть балки находилась в равновесии, нужно соблюдение нулю суммы проекций
сил на ось Y и суммы моментов относительно точки К, т.е. |
|
Y= 0; |
(11.1) |
MK = 0. |
(11.2) |
В сечении 1-1 действуют внутренние напряжения. Касательные |
|
напряжения в сумме равны внутренней поперечной силе Q, т.е. |
|
S = Q , |
(11.3) |
118
где S – площадь поперечного сечения балки. Нормальные напряжения, о которых подробно будет рассмотрено ниже, создают внутренний изгибающий момент Ми.
|
|
Проектируя силы на ось Y, |
|||||
|
получим, учитывая, что отсеченная |
||||||
|
часть балки АК находится в |
||||||
|
равновесии (покое), |
|
|
|
|
||
|
RA - Q = 0, |
|
|
|
(11.4) |
||
|
что |
соответствует |
|
требованию |
|||
|
(11.1) и из которого находим |
|
|||||
|
Q = RA. |
|
|
|
(11.5) |
||
|
|
Составляя |
|
уравнение |
|||
|
моментов относительно точки К и |
||||||
|
учитывая, что часть балки АК |
||||||
|
находится в равновесии, получаем |
||||||
|
- RA х + Ми = 0, |
|
|
(11.6) |
|||
|
откуда |
|
|
|
|
|
|
|
Ми = RA x. |
|
сила |
(11.7) |
|||
|
|
Поперечная |
Q |
и |
|||
|
изгибающий |
момент |
|
Ми |
|||
|
называются внутренними силовыми |
||||||
|
факторами, |
которые |
|
являются |
|||
|
результатом |
действия |
внутренних |
||||
|
молекулярных сил. |
|
|
|
|
||
|
|
Знаки |
внутренних |
силовых |
|||
|
факторов определяются следую- |
|
|||||
Рис.11.1 |
щим образом. |
|
|
|
|
||
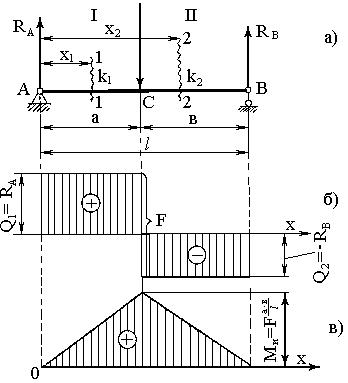
Если моменты М от внешних сил |
|||||||
изгибают |
балку |
выпуклостью |
вниз |
||||
(рис.11.2,а), когда растянутые волокна |
|||||||
расположены |
снизу, а |
сжатые |
– |
сверху, |
то |
||
изгибающий (внутренний) момент Ми имеет знак плюс (+).
Если моменты М от внешних сил изгибают балку выпуклостью вверх, когда растянутые волокна находятся сверху, то изгибающий момент Ми имеет знак минус (-) (рис.11.2,б).
Если внешние силы Р поднимают левую
Рис.11.2
119
и опускают правую часть балки, то поперечная сила Q имеет знак плюс (+) (рис.11.2,в).
Если внешние силы Р стремятся опустить левую и приподнять правую часть балки, то поперечная сила Q имеет знак минус (-).
11.2. Эпюры изгибающих моментов и поперечных сил
Законы изменения внутренних силовых факторов: изгибающих моментов и поперечных сил, которые определяются уравнениями, где функциями являются Q и Ми, а аргументом – абсцисса Х, удобно представлять в виде графиков, ординаты которых для любого значения абсциссы Х дают соответствующие значения изгибающего момента М или
поперечной силы Q. Такие графики называются эпюрами. При построении эпюр положительные значения М и Q откладывают вверх от оси абсцисс, а отрицательные – вниз.
Построение эпюр имеет целью определить опасное сечение, где внутренние силовые факторы достигают своего максимума.
Рассмотрим несколько примеров построения эпюр изгибающих моментов и перерезывающих сил.
Рис.11.3
Для определения опорных реакций RА и RВ составим уравнения равновесия, приравняв нулю сумму моментов всех внешних сил относительно точек А и В.
МА = RB l - Fa = 0; |
|
||||
MB = -RA l +Fb = 0. |
|
||||
Затем найдем опорные реакции |
|
||||
RB F |
a |
; |
(11.8) |
||
|
|
||||
|
|
l |
|
||
RA F |
b |
. |
(11.9) |
||
|
|||||
|
l |
|
|||
120
Для проверки составим уравнение равновесия проекций всех сил на
ось Y |
|
Y = RA +RB - F = 0. |
(11.10) |
Если после подстановки в уравнение (11.10) значений всех сил оно |
|
не обращается в нуль, то нужно искать ошибку в расчетах реакций опор. Разбиваем балку на два участка: I-й участок – АС; II-й участок – СВ. На I-м участке сделаем произвольное сечение балки 1-1 на
расстоянии х1 от точки А, а затем мысленно отбросим часть балки справа
от сечения. На оставшейся части балки АК1 длиной х1 |
действует внешняя |
|||||||
сила RA (см. рис.11.1,в), а в сечении балки действуют внутренние силовые |
||||||||
факторы: поперечная сила Q1 |
и изгибающий момент Ми1. Знак |
|||||||
изгибающего |
момента |
будет |
|
положительный |
(рис.11.2,а) |
и |
||
перерезывающией силы – тоже положительный (рис.11.2,в). |
|
|||||||
Поперечная сила в любом сечении на участке I от х1=0 до х1=а равна |
||||||||
реакции RA согласно уравнению (11.4) и (11.5), |
|
|
||||||
|
|
Q R |
A |
F |
b |
. |
(11.11) |
|
|
|
|
||||||
|
|
1 |
|
l |
|
|
||
|
|
|
|
|
|
|
||
Поперечная сила постоянна по всей длине участка. На эпюре (рис.11.3,б) от оси 0-х откладываем ординату Q1=RA на I-м участке и проводим прямую, параллельную оси 0-х. Получаем эпюру поперечных сил на участке I. Площадь, занимаемая эпюрой, заштрихована вертикальными линиями и в кружочке поставлен знак (+).
Найдем выражение изгибающего момента в любом сечении на первом участке при изменении х1 в пределах от х1=0 до х1=а. Составим уравнение моментов относительно точки К1 (11.6), откуда получим
M |
u1 |
R |
A |
x |
|
Fb |
x . |
(11.12) |
|
||||||||
|
|
1 |
|
l 1 |
|
|||
Согласно принятому правилу знаков изгибающий момент положителен, т.к. сила RA изгибает балку выпуклостью вниз (рис.11.2,а). Изгибающий момент является функцией аргумента х1, поэтому график будет иметь вид прямой линии. При х1=0; Ми1=0. При х1=а; Ми1=RA; а = Fab/l. Откладываем на эпюре (рис.11.3,в) эти ординаты и их концы соединяем прямой линией. Получаем эпюру изгибающих моментов на участке I.
На участке II сделаем произвольное сечение балки 2-2 на расстоянии х2 от точки А, а затем мысленно отбросим часть балки справа от сечения. На оставшейся части балки АК2 длиной х2 действуют силы RA и F, а в сечении балки действуют внутренние силовые факторы: поперечная сила Q2 и изгибающий момент Ми2.
Поперечная сила в любом сечении на участке II от х2=а до х2=l определится из уравнения равновесия (с использованием уравнения
(11.10)):
