
1798
.pdf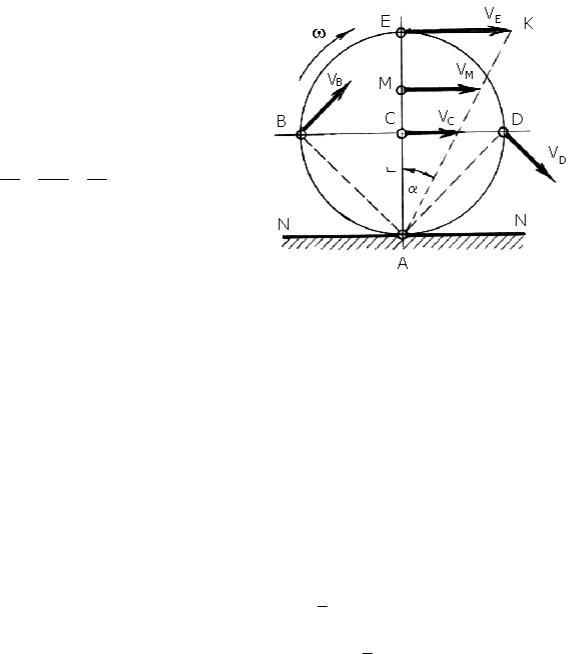
41
Точка тела, скорость которой в данный момент равна нулю,
называется мгновенным центром скоростей, или мгновенным центром вращения.
Линейная скорость любой точки тела (круга) в каждый момент времени равна произведению угловой скорости тела (круга) на радиус данной точки от центра вращения и направлена перпендикулярно этому радиусу в сторону вращения тела (круга):
vC r ; vE 2r ; vM AM
и т.д. Скорости точек, принадлежащих прямой AE (диаметру), вписываются в треугольник AEK, т.к. на основании подобия треугольников
vC vM vE tg . r AM 2r
Пример 1. Колесо радиуса |
|
r = 1 м катится по прямому |
|
рельсу. Скорость центра С колеса |
|
vC = 1 м/с. |
Рис.2.11 |
Определить угловую скорость колеса и скорости точек B, D, E (рис.
2.11).
Р е ш е н и е
Угловую скорость определим по формуле (2.33)
|
vс |
|
2 |
2 рад/с . |
|
|
|||
|
r 1 |
|
||
Радиус точки Е относительно точки А равен диаметру колеса, то есть 2r, поэтому линейная скорость точки Е
vE 2r 2 2 1 4 м/с .
Радиусы точек B и D определятся из прямоугольных равнобедренных треугольников ABC и ACD:
AB AD r
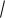 2 1,41 м .
2 1,41 м .
Теперь найдём линейные скорости точек B и D
vB vD AB r
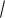 2 2,82.
2 2,82.
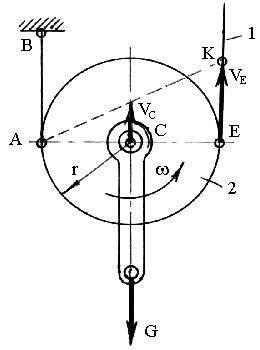
Пример 2. Определить (рис. 2.12) скорость подъема груза G, если скорость подъема каната 1, поднимающего блок 2 vE 16 м/мин, а радиус блока r 0,1 м.
42
Р е ш е н и е
Канат 1 переброшен через блок 2 и закреплен другим концом в точке В. Ветвь каната АВ неподвижна, поэтому блок 2 катится по неподвижной ветви каната АВ как по рельсу, аналогично кругу на рис. 2.11.
Радиус точки Е относительно точки А равен диаметру блока 2r. Определим угловую скорость блока (vE
16 м/мин 2,67 м/с).
|
vE |
|
2,6 |
1,33 рад/с . |
2r |
|
|||
|
|
2 0,1 |
||
Точка С будет подниматься вместе с грузом G. Скорость точки С, то есть скорость подъема груза, равна
vC r 1,33 0,1 0,133 м/с 8 м/мин.
Рис.2.12
3. ДИНАМИКА
3.1.Основные понятия и аксиомы динамики
Раздел теоретической механики, в котором устанавливается и изучается связь между движением тел и действующими на них силами, называется динамикой.
Вдинамике решаются две основные задачи:
1.Прямая задача. По известным действующим на тело силам определяются параметры движения тела.
2.Обратная задача. По известному закону движения тела определяются силы, действующие на него.
Примеры. 1. Полет снаряда. Даны силы F и G. Определяются траектория, скорость, ускорения (прямая задача).
2.Движение поезда. Заданы путь, скорость, ускорение. Определяются силы (обратная задача).
Воснове динамики лежат законы Ньютона, опубликованные в его “Математических началах натуральной философии” в 1687 г.

43
Эти законы являются аксиомами динамики и объективными законами природы, которые были установлены на основании многочисленных опытов и наблюдений Ньютона и его предшественников.
Первая аксиома (I закон Ньютона) – закон инерции: материальная точка сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие других тел не изменит этого состояния.
Свойство материальной точки или тела сохраняет постоянство скорости v const (v 0) и называется инертностью или инерцией.
Движение материальной точки или тела, не подвергающихся воздействию сил, называется движением по инерции.
Если скорость тела v 0, то это состояние покоя или статического равновесия. Если скорость тела v 0, но v const, то это состояние
динамического равновесия.
Вторая аксиома (II закон Ньютона) – основной закон динамики:
ускорение, сообщаемое материальной точке (или телу), приложенной к ней силой, пропорционально модулю силы и совпадает с ней по направлению.
Основное уравнение динамики имеет вид
F m a . |
(3.1) |
Все физические величины, входящие в формулу (3.1), имеют самостоятельное определение. Определение силы F описано в статике, определение ускорения а – в кинематике. Опишем массу материальной точки m. Анализируя формулу (3.1), мы видим, что при увеличении массы нужно для разгона тела до одного и того же ускорения приложить большую силу. Чем больше масса, тем труднее вывести ее из состояния покоя или движения по инерции, например остановить катящийся по инерции вагон. Поэтому массу определяют как меру инертности тела.
Частный случай основного уравнения динамики:
G mg , |
(3.2) |
из которого определяют массу
m G g , |
(3.3) |
где m – масса тела; G – вес тела; g = 9,81 м/с2 – ускорение свободного падения тел в пустоте.
За единицу массы в СИ принят килограмм (1 кг), который согласно формуле (3.3) равен
1кг |
1Н |
1 |
Н с2 |
|
|
|
. |
||
1м c2 |
|
|||
|
|
м |
||
44
Третья аксиома (III закон Ньютона) – закон равенства действия и противодействия: действию одного тела всегда соответствует равное ему и противоположно направленное противодействие другого тела, то есть действие двух тел друг на друга всегда равны и направлены по одной прямой в противоположные стороны.
Эта аксиома соответствует 5 аксиоме статики.
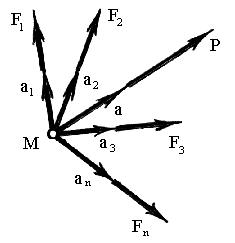
Четвертая аксиома – принцип (закон) независимости действия сил: при одновременном действии на материальную точку нескольких сил они сообщают ей ускорение, равное геометрической сумме тех ускорений, которые точка получила бы при действии каждой из этих сил в отдельности.
ma F1 F2 F3 ... Fn P. |
(3.4) |
В самом деле, F1 m a1 ; F2 m a2 и т.д. Тогда
ma=ma1+ma2+ma3+…+man . (3.5)
Формула (3.5) показывает, что равнодействующее ускорение, если сократить формулу (3.5) на m, равно геометрической сумме ускорений
a=a1+a2+a3+…+an . (3.6)
Ускорения a1, a2 и т. д. материальная точка получает от действия сил F1 и F2 и т.д. Сравнивая уравнения (3.4), (3.5) и (3.6), видим: равнодействующее ускорение a (формулы (3.5) и (3.6)) то же самое ускорение, что ускорение a, которое создает
равнодействующая сил P (формула (3.4)). На рис. 3.1 показано, что вектор
равнодействующего ускорения а, полученный геометрическим сложением ускорений a1 + а2 + a3 + an, совпадает по направлению с равнодействующей Р, которая является геометрической суммой сил F1 + F2 + F3 + F4 = Р.
Основной закон динамики, при условии действия на материальную точку нескольких сил, можно записать в общем виде
n |
(3.7) |
Fi |
ma. |
i 1 |
|
45
Если материальная точка несвободна и имеет связи, то освободив ее от связей и заменив их реакциями, движение точки можно считать как свободное, а уравнение (3.7) примет вид
n k
Fi Ri ma,
i 1 i 1
где Fi – внешние силы ; Ri – реакции связей.
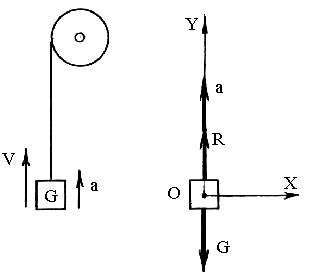
Пример 1. Груз G поднимают с ускорением а. Определить натяжение каната R.
Р е ш е н и е
Поднимаемый груз G примем за материальную точку О. Выберем систему координат XOY, ось Y которой совпадает с ускорением а.
Освобождая материальную точку (груз) от связей (каната), заменим канат (связь) реакцией R.
(3.8)
Рис.3.2
Запишем основной закон динамики для несвободной материальной
точки:
R – G = m a ,
где R – реакция каната; G = m g – вес груза; m – масса тела (груза); а – ускорение.
Подставив значение груза G в уравнение и решив его относительно R, получим
R = ma + mg = m ( a + g).
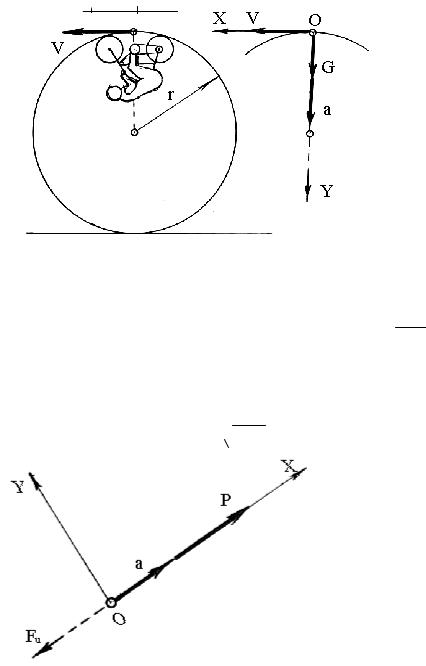
Пример 2. Какова должна быть скорость велосипедиста, чтобы пройти “мертвую петлю” радиусом r?
Р е ш е н и е Принимаем велосипедиста с велосипедом за материальную точку.
Систему координат XOY располагаем таким образом, чтобы ось OY совместилась с ускорением an. При равномерном движении материальной точки по окружности тангенциальное (касательное) ускорение at = 0. Поэтому полное ускорение а равно нормальному (центростремительному) ускорению, то есть а = аn .
46
Рис.3.3
Согласно основному закону динамики
G = m a = m an .
Именно сила веса
вданном случае является движущей силой, которая вызывает ускорение а, но
всвою очередь G = mg. Подставив значение G и
an v2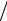 r в основное уравнение и решив его
r в основное уравнение и решив его
относительно скорости, получим
g an v2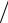 r ; g v2
r ; g v2 r ; v
r ; v 
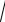 g r .
g r .
Из полученного уравнения видно, что если нормальное ускорение равно ускорению свободного падения, то наступает равновесие, которому
соответствует скорость v 
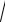 g r. На этом задача окончена.
g r. На этом задача окончена.
Вернемся к рис. 3.1. Равнодействующая сила Р = F1 + F2 + . . . + Fn сообщает материальной точке ускорение а. Расположим систему координат таким образом, чтобы ось OX совпала с ускорением а (рис. 3.4).
Среди действующих сил могут быть активные силы Fi и реакции
связей Ri, т.е.
Рис.3.4
n k
P Fi Ri .
i 1 i 1
Согласно основному закону динамики
P = m a .
Перенесем вектор ma в левую часть уравнения, получим
P m a 0 . |
(3.9) |
47
Вектор m a имеет размерность силы.
Что же представляет собой эта сила? Вопервых, наличие этой силы уравновешивает систему сил F1 + F2 + . . . + Fn = Р . Вовторых, сила m a имеет знак минус, поэтому она направлена в сторону, обратную равнодействующей Р и ускорению а. В - третьих, по величине (модулю) эта сила равна равнодействующей Р.
Сила, равная по величине произведению массы материальной точки на ее ускорение, но направленная в сторону, противоположную ускорению, называют силой инерции.
Fu = m a . |
(3.10) |
На основании сказанного можно сделать вывод, который называется принципом Даламбера:
Силы, приложенные к материальной точке, уравновешиваются силой инерции
|
n |
k |
|
|
P Fu |
Fi |
Ri Fu |
0. |
(3.11) |
|
i 1 |
i 1 |
|
|
Полученную систему сил можно рассматривать как находящуюся в равновесии, а уравнение (3.11) уравнением равновесия. Такое равновесие называют динамическим.
Силы инерции действительно существуют. Достаточно вспомнить поездку в автобусе или троллейбусе. При трогании с места в период разгона ускорение направлено вперед, но нас сила инерции тянет назад. При резком торможении ускорение направлено назад, но нас сила инерции толкает вперед.
Принцип Даламбера позволяет при решении задач динамики использовать уравнение равновесия статики. Такой метод носит название
кинетостатики.
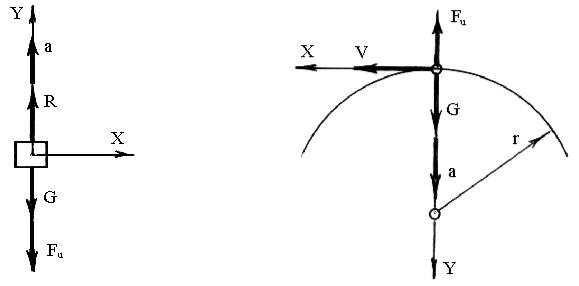
Решим примеры 1 и 2 (рис. 3.2 и 3.3) методом кинетостатики. Пример 1. Чтобы уравновесить силу G и реакцию R, приложим
силу инерции Fu = m a (рис. 3.5).
|
Уравнение равновесия будет иметь вид |
|
|
R G +F = 0 , |
(3.12) |
или |
R m g |
|
|
|
|
где |
ускорение g и сила |
|
оси |
– сила инерции |
, |
|
OY. |
|

48
Рис.3.5 |
Рис.3.6 |
Из уравнения (3.13) находим
R = m g + m a = m (g + a) .
Нужно помнить, что сила веса G – движущая сила и всегда совпадает по направлению с вызванным ускорением g, согласно основному закону динамики. Сила инерции – реактивная сила, которая порождается ускорением а и всегда направлена в сторону, обратную ускорению.
Пример 2. Чтобы уравновесить силу G (рис. 3.3), приложим силу инерции Fu = m a (рис. 3.6).
Уравнение равновесия будет иметь вид
G +Fи = 0 ,
или
m g m a g a 0 ,
где G = m g, так как ускорение g и сила G направлены в сторону оси OY; Fи = ma – сила инерции, которая направлена в сторону, противоположную оси OY.
При равномерном движении по окружности
a an v2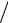 r.
r.
После подстановки получим
v 
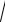 g r .
g r .
3.2. Работа и мощность
49
3.2.1. Работа постоянной силы при прямолинейном движении
Для оценки и характеристики действия силы, которая перемещает тело или материальную точку с постоянной скоростью, вводят понятие о мере этого действия – работа силы.
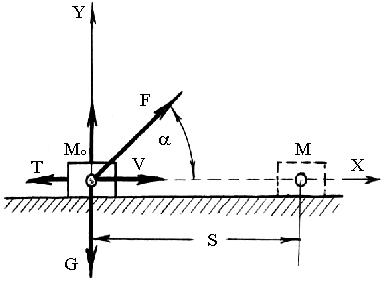
Пусть на тело (рис. 3.7) действует сила F, которая, преодолевая сопротивление трения Т, двигает тело по плоскости со скоростью v из положения M0 в положение M .
Разложим силу F на две составляющие. Вдоль оси X будет действовать составляющая Fx = F · cos , а вдоль оси Y будет действовать составляющая Fy = F · sin .
Составим два уравнения равновесия
X F · cos – T = 0 ;
Y F · sin – G+R = 0 .
Из этих уравнений определяются реакция плоскости на тело R и сила трения Т при заданных F и G.
Реакция R вызывает силу трения T f R, а составляющая
Fx=Fcos движет тело, преодолевая трение Т. На это перемещение затрачивается энергия, которая называется работой. Это понятие вводится для оценки действия силы. Мерой этого действия является работа силы, величина которой равна произведению силы на пройденный путь.
Величина работы определяется по формуле
A=Fcos · s , |
(3.14) |
где А – работа силы; F – сила, действующая на тело; – угол между направлением силы и скорости тела. Если 0, то формула (3.14) примет вид
A F s. |
(3.15) |
Работа – скалярная величина. Она измеряется в джоулях: 1 Дж =

50
1 Н м.
Сила, направленная против движения, называется силой сопротивления (трение, сопротивление воздуха, сила сопротивления при вспашке земли и т.д.). Различают силы полезного и вредного сопротивлений.
Сила полезного сопротивления – сила технологического сопротивления рабочего органа машины: сила подъема груза, сила сопротивления плуга, сила забивания сваи и т.д.
Сила вредного сопротивления – это сила трения, сила сопротивления воздуха или воды и т.д.
3.2.2. Мощность и коэффициент полезного действия
Два человека копают огороды по 500 м2 каждый. Один вскопал огород за полдня, а другой – за день. Кто из них более работоспособен, более мощный? То же можно сказать о тракторах. Следовательно, знание только величины работы для оценки работоспособности недостаточно. Для характеристики быстроты совершения работы вводится понятие мощности.
Мощностью называется величина, выражающая работу, произведенную в единицу времени.
N A t . |
(3.16) |
Если сила совпадает с направлением движения (3.15), то мощность можно определить по формуле
N F s F v. |
(3.17) |
t |
Единицей мощности в системе СИ является ватт:
1Вт 1Дж 1Н м .
сс
Втехнике применяется единица мощности, именуемая лошадиной
силой, 1 л.с. = 75 кгс м/с .
1 л. с. = 736 Вт = 0,736 кВт . 1 кВт = 1,36 л. с.
Если машина работает с постоянной мощностью, то работа, совершаемая за время t, равна
A = N t .
