1798

31

Переходя к пределу при t 0, т.е. приближая бесконечно точку А1 к точке А, найдем вектор истинного ускорения

Вектор ускорения а характеризует как изменение численного значения скорости, так и изменение ее направления.

По аналогии можно записать

где аt – вектор касательного или тангенциального ускорения, которое изменяет численное значение скорости; аn – вектор нормального или центростремительного ускорения, которое всегда направлено по радиусу к центру дуги и оно изменяет направление скорости.

В дифференциальной форме уравнения (2.6) и (2.8) запишутся в

виде

Если кривую а – а на рис. 2.5 и 2.6 выпрямить, то тогда тангенциальные сос-тавляющие v = vt; а = аt, а нормальные состав-ляющие vn = 0; аn = 0.

Рис.2.6

32

2.2.Равнопеременное движение

2.2.1.Прямолинейное движение

Неравномерное движение с постоянным ускорением называется

равнопеременным.

Пусть материальная точка движется прямолинейно вдоль оси ОX от точки А, которая соответствует начальному положению t0 = 0. Путь в

Путь, скорость и ускорение - величины алгебраические. Они могут иметь положительное и отрицательное значения. Отрицательное значение пути показывает, что он отмеряется влево по рис. 2.7. Отрицательная скорость означает, что она направлена влево по рис. 2.7. Отрицательное ускорение означает, что движение материальной точки равнозамедленное. Если v = 0, то точка останавливается. Если а = 0, то движение равномерное.

Ускорение точки в дифференциальной форме имеет вид

a dv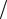dt .

Откуда приращение скорости

dv = a d t .

Интегрируя в пределах от t0 до t, получим

v t t

Подставив значение v в уравнение (2.11), получим

33

ds = v0 dt + at dt .

Проинтегрируем

s t t

ds υ0 dt a t dt .

Уравнения (2.11) и (2.13) являются основными уравнениями равнопеременного прямолинейного движения. Из уравнения (2.11) можно определить ускорение

Средняя скорость определяется как среднее арифметическое между начальной и конечной скоростями

Пример. Задан закон движения материальной точки. Заданное

уравнение имеет вид

s = 5 – 9t + 3t2 .

Определить скорость и ускорение материальной точки и проанализировать уравнения.

Проанализируем заданное уравнение. В начальный момент t0 = 0. Подставив значение t0 в заданное уравнение, получим

s = s0 = 5 .

Продифференцировав заданное уравнение, получим

Проанализируем уравнение (2.14). В начальный момент при t0 = 0 скорость v0 = 9, т.е. скорость отрицательна. Это говорит о том, что в начальный момент точка двигалась назад в отрицательном направлении. Приращение скорости 6t = v – положительное, поэтому должен наступить момент, когда скорость станет равной нулю, т.к. сравняются отрицательная начальная скорость v0 и приращение скорости v. Если в уравнении (2.14) скорость приравнять нулю, то получим

v = v0 + v = 9 + 6 t = 0 ;

откуда

Во время движения tс материальная точка остановится в положении С, т.к. ее скорость станет равной нулю, а затем начнет двигаться в положительном направлении, т.к. в уравнении (2.14) положительное приращение скорости v = 6t будет больше по величине отрицательной начальной скорости v0 = 9. Например, в момент, когда t = 2c, скорость v = 9 + 6 2 = + 3.

Чтобы определить ускорение, нужно продифференцировать уравнение (2.14)

Построим графики пути, скорости и ускорения в координатах tOs; tOv и tOa в соответствии с уравнениями

s = 5 9t + 3t2 ;

v = 9 + 6t ; (2.13, 2.14, 2.16) a = 6 .

Построение начинаем с определения опорных точек. В начальный момент времени (рис. 2.8):

путь s0 = 5 соответствует точке А;

скорость v0 = 9 соответствует точке А' ;

ускорение а = 6 соответствует точке А''.

На графике пути видно, что материальная точка из положения А (ордината Os) начинает двигаться в отрицательном направлении до точки С1. При этом скорость благодаря положительному ускорению возрастает

35

от положения А' до положения С', в котором скорость vс = 0 и материальная точка остановится. Время, соответствующее этой точке, равно tс = 1,5. Подставив это время в уравнение (2.13), получим

sc = 5 – 9 · 1,5 + 3 ·1,52 = 1,75 .

Откладываем расстояния tс и sс на графике пути и получаем точку C, а на графике скорости для времени tc = 1,5 намечаем точку С', соответствующую скорости

vс = 0.

Уравнение (2.14) первой степени, поэтому график скорости – прямая линия, для проведения которой достаточно иметь две точки А' и С'.

Уравнение (2.16) есть константа, поэтому график параллелен оси абсцисс и для его построения достаточно иметь одну точку А".

Уравнение (2.13) второй степени описывается параболой, для построения которой нужно больше точек. При движении из начального положения А (s0 = 5) материальная точка проходит через начало координат и из положительной области заходит в отрицательную область, т.е. проходит через положение О. Приравняв нулю уравнение

(2.13), получим

s = 5 9t + 3t2 = 0 .

t 9 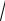92 4 3 5 ;

2 3

tB = 0,74; tD = 2,26; sB = sD = 0 .

На графике пути отмечаем точки В и D.

36

Плавно соединяя точки, получаем график пути - параболу ABCD. С помощью приведенных графиков удобно анализировать движение материальной точки и его параметры.

2.2.2. Криволинейное движение

При криволинейном движении скорость и ее вектор величины переменные, которые изменяются по численной величине (модулю) и по направлению. Вектор скорости в любой момент времени направлен по касательной к траектории движения материальной точки и перпендикулярен к радиусу дуги траектории. Поэтому скорость материальной точки всегда касательная или тангенциальная к траектории v = vt .

Ранее было показано (рис. 2.5 и 2.6), что касательное ускорение

где r- радиус кривизны в данной точке.

Из рис. 2.6 видно, что модуль полного ускорения можно определить по теореме Пифагора

a at2 an2 .

(2.19)

Путь при равнопеременном криволинейном движении определяется по формуле

От уравнения (2.13) формула (2.20) отличается ускорением. Дело в том, что при прямолинейном движении an = 0 и a = at.

Если продифференцировать уравнение (2.20), то получим формулу для скорости

Видим, что уравнения (2.11) и (2.21) идентичны.

37

Уравнения (2.17...2.21) являются основными уравнениями неравномерного криволинейного движения материальной точки.

2.3.Вращение тела вокруг неподвижной оси

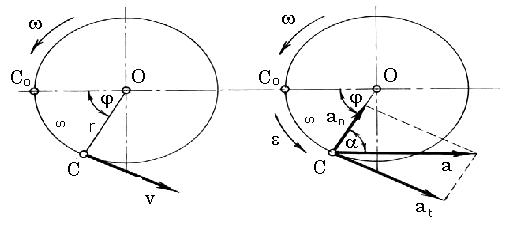
Когда тело вращается вокруг неподвижной оси, все его точки (например, точка С на рис. 2.9) вращаются вокруг этой оси и описывают окружности, которые являются траекториями этих точек.

Вращательное движение твердого тела характеризуется углом поворота (рис. 2.9). Пусть в начальном положении t0 = 0 вертикальная плоскость ACB занимала положение, соответствующее точке С0. При вращении тела плоскость ACB займет новое положение, повернувшись вокруг оси Z на угол .

Угол называется углом поворота тела. Он измеряется в радианах. Угол поворота играет ту же роль при вращении тела, что пройденный путь s при движении материальной точки.

Чтобы изучить вращательное движение тела, нужно задать угол поворота как функцию времени

Это уравнение называют законом вращательного движения тела вокруг неподвижной оси.

Проводя аналогию между движением материальной точки и вращением твердого тела, можем записать

Средняя скорость равномерного вращения

38

равна отношению приращения угла поворота к приращению времени

t.

Измеряется угловая скорость в радианах в секунду (1 рад/с или 1c-1), так как радиан безразмерная величина. Угол поворота в технике измеряют количеством оборотов N тела вокруг оси Z, поэтому, учитывая, что

1об.=2 ,

Угловую скорость в технике задают числом оборотов в минуту, т. е. частотой вращения n. Следовательно, если умножим 2 на n, то получим 2 n рад/мин, а чтобы перейти к секундам, нужно еще разделить на 60. Тогда получим

При грубых и прикидочных расчетах допускается

С помощью формулы (2.26) заданную частоту вращения тела можно перевести в угловую скорость, и наоборот.

При равномерном вращении = const угол поворота определяют по формуле

При равнопеременном вращении угловая скорость в единицу времени изменяется на одинаковую величину. Быстрота изменения угловой скорости во времени характеризуется угловым ускорением . Угловое ускорение вращательного движения тела равно первой производной от угловой скорости по времени

Угловое ускорение измеряют в радианах в секунду в квадрате (1 рад/с2 или 1 с-2).

При равнопеременном вращении const. Уравнения равнопеременного вращения тела аналогичны уравнениям (2.11) и (2.13) равнопеременного движения материальной точки

где 0 – начальный угол поворота, который предшествовал начальному положению тела при t0 0; 0 – начальная угловая скорость при t0 0.

Угол поворота, угловая скорость и угловое ускорение – величины алгебраические. Они могут иметь положительное и отрицательное значения. Угол поворота считают положительным (рис. 2.9) при вращении тела против часовой стрелки, если смотреть на тело с конца оси вращения Z, то есть со стороны стрелки оси. При вращении тела по часовой стрелке угол поворота считают отрицательным. Угловая скорость будет положительной, если тело при этом вращается против часовой стрелки, и отрицательной, если – по часовой. Угловое ускорение будет положительно, если оно сообщает ускоренное вращение телу, и отрицательно, если оно сообщает замедленное вращение телу.

Рассмотрим движение любой точки С тела, вращающегося вокруг неподвижной оси Z (рис. 2.9).

Рис.2.10

Твердое тело состоит из множества материальных точек. Каждая точка движется вместе с телом, поэтому для всех точек тела общими характеристиками вращательного движения являются угол поворота , угловая скорость и угловое ускорение . Траектории всех точек тела при вращении вокруг неподвижной оси являются окружностями, расположенными в плоскостях, перпендикулярных к оси вращения Z.

Взаимосвязь (рис. 2.10) между углом поворота , радиусом окружности r и длиной пути материальной точки по окружности s выражается формулой

40

Таким образом, зная угол поворота и радиус окружности, определяют путь материальной точки.

Скорость точки тела, вращающегося вокруг оси, называется линейной, в отличие от угловой скорости тела. Дифференцируя уравнение (2.32) по времени и учитывая формулы (2.12) и (2.23), получим

Линейная скорость материальной точки, движущейся по окружности, равна произведению угловой скорости тела на радиус окружности.

Касательное, или тангенциальное, ускорение точки тела, вращающегося вокруг оси, изменяет линейную скорость точки и определяется по формулам (2.17), (2.29) и (2.33):

Нормальное, или центростремительное, ускорение точки вращающегося тела изменяет направление линейной скорости точки и находится по формулам (2.18) и (2.33):

Полное ускорение определим, используя формулу (2.19):

Направление вектора полного ускорения можно определить по углу, образованному вектором a и радиусом r:

Круг ABED радиусом r катится по прямой N–N (рис. 2.11) с угловой скоростью . Аналогом может быть колесо велосипеда, автомобиля и т.д. Круг касается прямой N–N в точке А, которая принадлежит одновременно неподвижной прямой N–N и кругу. Эта точка касания А в данный момент является неподвижной, а весь круг вращается относительно точки А с угловой скоростью , поэтому все точки круга вращаются также относительно точки А.