
1798
.pdf
|
|
|
21 |
|
Из сказанного выше |
можно |
|
||
сделать вывод: пара сил может |
|
|||
только вращать тело, не передвигая |
|
|||
его в сторону ( на рис. 1.20 тело |
|
|||
вращается по часовой стрелке). |
|
|||
Кратчайшее |
расстояние |
|
||
между линиями действия пары сил |
|
|||
называют плечом пары. |
|
|
|
|
Формула |
(1.17) |
показывает, |
|
|
что вращательное действие пары сил |
|
|||
зависит как от величины силы F, так |
|
|||
и от расстояния между ними а. |
|
|||
Момент |
пары |
условимся |
|
|
считать положительным, если он |
|
|||
стремится повернуть |
тело против |
|
||
часовой стрелки и отрицательным, |
Рис.1.20 |
|||
если - по часовой стрелке. |
|
|
||
Пусть |
рычаг |
AB |
может |
|
вращаться вокруг точки A (рис. 1.21, а). |
|
|||
Что будет происходить с рычагом, если |
|
|||
к нему приложить силу F в точке B? |
|
|||
На основании третьей аксиомы, |
|
|||
не нарушая механического равновесия |
|
|||
твердого тела, приложим к нему две |
|
|||
уравновешенные силы F в точке А, |
|
|||
которые параллельны заданной силе F |
|
|||
(рис. 1.21, б). |
|
|
|
|
В результате мы получим пару |
|
|||
сил F (силы перечеркнуты двумя |
|
|||
черточками), у которых момент равен |
|
|||
M = F (AB) = F a , |
|
|||
и силу F, перенесенную параллельно |
Рис.1.21 |
|||
самой себе из точки B в точку A. |
|
|||
В механике пользуются понятием момент силы относительно
точки.
Момент силы относительно точки определяется произведением модуля силы на длину перпендикуляра, опущенного из точки на линию действия силы.
Точка А (рис. 1.21), относительно которой берется момент, называется центром момента, а длина перпендикуляра a- плечом силы относительно центра момента.
22
Момент силы F относительно центра А обозначается
MA(F) = F a. |
(1.18) |
Момент силы измеряют в ньютонометрах (Н м).
Знак момента такой же, как у пары сил, т. е. плюс, если против часовой стрелки и, минус, если по часовой стрелке.
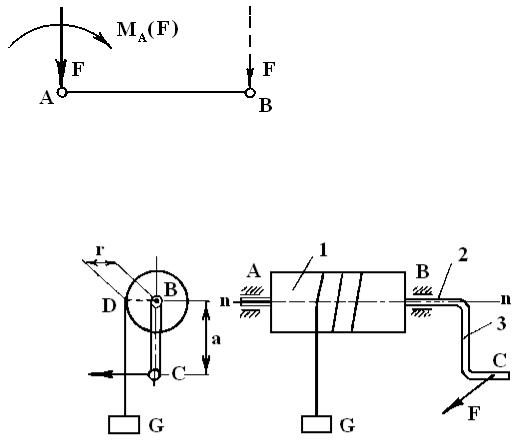
Таким образом, на основании выше изложенного можно сформулировать правило переноса силы в другую точку (рис. 1.22):
Чтобы перенести силу F из точки B в точку А, нужно приложить в точке А силу F, не меняя направления и модуля, и момент силы F
относительно точки А, MA (F).
Такой перенос силы называется приведением силы к другой точке. Этим правилом широко пользуются в статике.
Рис.1.23
Когда линия действия силы проходит через центр (точку А), ее момент относительно этой точки равен нулю, так как в данном случае плечо a = 0.
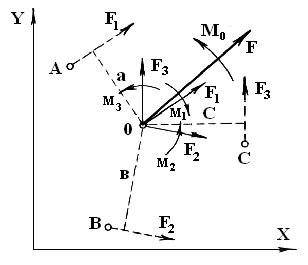
Колодезный ворот (рис. 1.23) состоит из барабана 1, оси 2, установленной в опорах A и B, и рукоятки 3. При подъеме груза G момент, создаваемый грузом G, равен моменту, создаваемому силой F, приложенной к рукоятке.
При равномерном движении барабан является рассматриваемым нами телом, и при его остановке, согласно аксиоме 1, он должен находиться в равновесии. Поскольку в данном случае движение вращательное, его силовым фактором является момент. Вращение происходит вокруг оси n-n (правая проекция рис. 1.23), которая на левой проекции проектируется в точку B. Рассмотрим равновесие барабана на
23
левой проекции. Центром вращения и центром моментов служит точка B. Момент, создаваемый грузом G относительно точки B,
MB (G) = G r |
(1.19) |
имеет положительный знак (плюс). Момент, создаваемый силой руки F, приложенной к рукоятке в точке С, относительно точки B
MB (F) = F · a |
(1.20) |
имеет отрицательный знак (минус). Сумма моментов относительно точки В
MB MB(G) MB(F) G r F a 0 |
(1.21) |
равна нулю, т.к. система находится в равновесии.
Уравнение (1.21) является третьим уравнением равновесия плоской системы, когда силы приложены к телу произвольно.
Часто бывает необходимо привести несколько сил к одной точке. Пусть даны силы F1; F2 и F3, приложенные в точках A, B и C. Требуется перенести эти силы в точку О.
Пользуясь правилом (рис. 1.22), переносим силу F1 из точки A в точку O и прикладываем момент
M1 = F1 a .
Затем переносим из точки B в точку O силу F2 и прикладываем момент
M2 = F2 b .
И, наконец, переносим силу
F3 из точки С в точку О и прикла- Рис.1.24 дываем момент
M3 = F3 c .
Силы F1, F2 и F3 приложены к одной точке O, поэтому их можно сложить графическим методом. Сложив геометрически силы, получим равнодействующую F, называемую главным вектором:
n |
|
F= Fi . |
(1.22) |
i 1 |
|
Складывая алгебраически моменты составляющих сил относительно центра O, получим главный момент
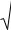
24
n |
|
M0 Mi . |
(1.23) |
i 1 |
|
Плоская система сил в результате приведения к данной точке O заменяется главным вектором и главным моментом.
Поскольку плоская система сил приводится к главному вектору и главному моменту, для обеспечения равновесия системы необходимо, чтобы главный вектор и главный момент равнялись нулю:
n |
n |
|
F Fi 0 ; |
M0 Mi 0 . |
(1.24) |
i 1 |
i 1 |
|
Эти уравнения называются векторными уравнениями равновесия.
Рассмотрим данную выше систему сил F1, F2 и F3 в координатных осях XOY (рис. 1.24).
Равнодействующая проекций сил на ось X определяется по формуле
|
|
n |
|
|
|
|
|
|
Fx Fxi . |
|
(1.25) |
||||
|
|
i 1 |
|
|
|
|
|
Равнодействующая проекций сил на ось Y определится по формуле |
|||||||
|
|
|
n |
|
|
|
|
|
Fy |
Fyi . |
|
(1.26) |
|||
|
|
i 1 |
|
|
|
|
|
Величина главного вектора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.27) |
|
F |
2 |
2 |
|
|
||
|
|
Fx |
Fy . |
|
|
||
Для обеспечения равновесия системы необходимо: |
|
||||||
n |
n |
|
|
|
|
n |
|
Fx xxi 0; Fy |
yyi 0; M0 |
Mi 0. |
(1.28) |
||||
i 1 |
i 1 |
|
|
|
|
i 1 |
|
Уравнения (1.28) называются уравнениями равновесия плоской системы, выраженные в аналитической форме. В дальнейшем для упрощения записей будем писать:
1. Сумма проекций на ось X равна нулю:
X 0. |
(1.29) |
2. Сумма проекций на ось Y равна нулю:
Y 0. |
(1.30) |
25
3. Сумма моментов относительно точки А равна нулю:
M A 0. |
(1.31) |
Уравнения (1.29 - 1.31) в дальнейшем будем называть уравнениями равновесия плоской системы сил.
.5. Составление уравнений равновесия
Встречается много задач, в которых тело представляет собой балку, установленную по концам на две опоры. В §1.3.5 приведен порядок решения задач, воспользуемся им.
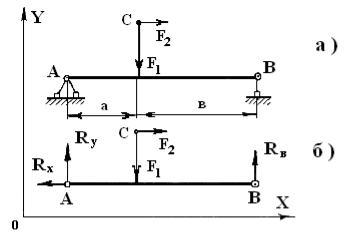
Пусть на балку AB (рис. 1.25, a), которая опирается на опоры A и B, действуют силы F1 и F2, приложенные в точке C жестко связанной с балкой AB. Все три точки AB и С принадлежат одному телу. Требуется определить реакции опор A и B.
Рис.1.25
Ре ш е н и е
1.Выделяем тело (балку ABC) и прикладываем к ней известные
силы F1 и F2 (рис. 1.25, б).
2.Освобождаем тело от связей и заменяем их действие реакциями. В точке А на балку (см. рис. 1.11) действуют две реакции Rx и Ry. Опора B может воспринимать только силу, которая действует вертикально, т.е. вдоль оси Y, а сила вдоль оси X может свободно, без сопротивления двигать точку В влево и вправо. Поэтому в точке В на балку действует реакция RB (рис. 1.25, б).
3.Выбираем координатную систему XOY и составляем три уравнения равновесия:
X F2 Rx 0;
Y Ry RB F1 0;
MA F1 h RB a b 0.

26
Примечание. Сумму моментов выгодно составлять относительно точки, в которой пересекаются или приложены две неизвестные реакции (или силы), тогда моменты этих сил относительно выбранной точки равны нулю и мы избавляемся в одном уравнении сразу от двух неизвестных. Общее число неизвестных не должно быть более числа уравнений статики, то есть трех.
4. Решение системы уравнений следует начинать с уравнения моментов, так как в нем содержится одна неизвестная. Решаем его относительно неизвестной RB :
RB F1a F2h . a b
Подставив значение RB во второе уравнение и решив его относительно Ry, получим
Ry F1 F1a F2h . a b
Решаем первое уравнение относительно Rx :
Rx F2.
2.КИНЕМАТИКА
2.1Основные понятия
Механическим движением называется перемещение одних тел относительно других в пространстве и во времени. При решении задач кинематики используются понятия о материальной точке и абсолютно твердом теле.
Материальная точка как объект исследования используется в том случае, когда форма тела и его размеры не влияют на изучение движения. Например, движение планет, движение самолета, поезда, автомобиля и т.д. В этих примерах используется кинематика точки.
Абсолютно твердое тело как объект исследования рассматривают в том случае, когда требуется исследовать относительное движение точек данного тела. Например, качение колеса по дороге, вращение маховика, движение шатуна двигателя внутреннего сгорания.
В этих примерах используется кинематика твердого тела, которая лежит в основе изучения вращательного и плоскопараллельного движений.
К основным понятиям кинематики относятся: направление движения, траектория движения, путь, пройденный материальной точкой,
27
время, затраченное на движение, скорость движения материальной точки, ускорение, то есть интенсивность изменения скорости.
Направление движения
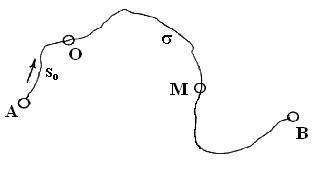
определяет, в какую сторону движется точка (от А к В или от В к А). Более строго, направление определяет вектор скорости, куда он направлен: вверх, вниз, влево, вправо.
Траектория движения –
это линия, которую описывает движущаяся точка в пространстве, т.е. след материальной точки.
Длина траектории при движении точки - это пройденный путь.
При движении по прямой путь равен расстоянию между начальной и конечной точками. При движении по кривой путь больше расстояния между точками
Скорость – это быстрота перемещения тел от одной точки пространства к другой. Она определяется величиной пути, проходимого точкой за единицу времени. Движение тела с постоянной скоростью называется равномерным, а с изменяющейся скоростью - переменным.
Величина, определяющая изменение скорости с течением времени, называется ускорением.
Изучение движения точки может начинаться от начала траектории (точка А на рис.2.1) или из произвольного положения О, в котором включается секундомер, т.е. отсчет времени. В этом случае вводится понятие начального пути s0 для определения исходного положения точки. Полный пройденный путь s будет определяться как алгебраическая сумма начального пути s0 и пройденного пути :
s s0 , |
(2.1) |
где s – путь, пройденный от начала отсчета А по кривой АМ; s0 – начальный путь, который пройден к моменту включения секундомера, измеряемый кривой АО; - пройденный путь за время t от точки О по кривой до точки М.
При движении точки по траектории путь s является функцией времени.
s = s(t). |
(2.2) |
Уравнение (2.2) выражает закон движения точки в общем виде. Материальная точка из положения О (рис. 2.1) может двигаться как
в сторону положения В, так и в сторону положения А.

28
Движение точки в сторону В будем называть положительным, а пройденный путь будет иметь знак плюс + . Движение в обратном направлении в сторону А будет отрицательным, а путь будет иметь знак минус .
Движение, при котором материальная точка за равные промежутки времени проходит одинаковые отрезки пути, называется равномерным движением.
Например, поезд каждый километр пути проходит за одинаковое время, следовательно, он движется равномерно.
Скорость равномерного движения определяется отношением пройденного пути ко времени.
v s t. |
(2.3) |
Скорость равномерного |
движе- |
ния всегда направлена в сторону движения. Скорость – векторная величина. Вектор скорости направлен по касательной к кривой в рассматриваемой точке (например, в точке М).
Путь, пройденный точкой с постоянной скоростью, пропорционален
времени движения: |
(2.4) |
= v t . |
Рис.2.2
Это основной закон равномерного движения. В общем случае, когда движение изучается с момента включения секундомера t0 = 0 в положении О (рис.2.1), основной закон записывается в виде
s = s0 + v t , (2.5)
где v t = – пройденный путь; v – скорость равномерного движения; t – время пройденного пути.
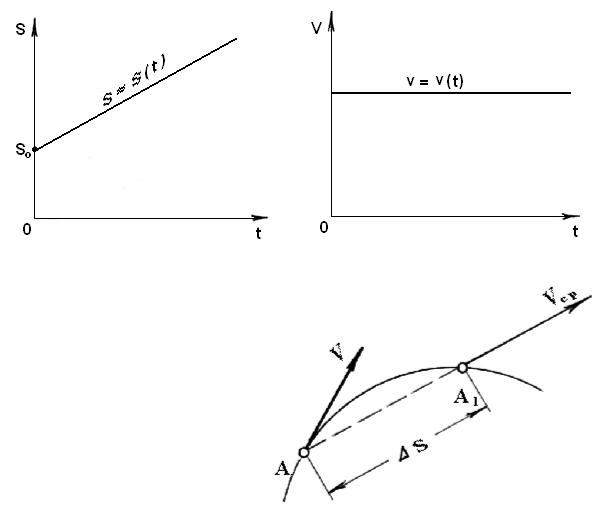
На рис. 2.3 приведен график пути и скорости в функции времени для равномерного движения.
Скорость измеряется в единицах пути, деленных на единицу времени – 1 м/с. Движение поезда измеряют в 1 км/ч = 0,278 м/с.
В общем случае материальная точка за равные промежутки времени проходит неравные отрезки пути, поэтому такое движение называют
неравномерным.
Пусть материальная точка перемещается из положения А по дуге. За время t точка из положения А переместится в положение А1. Если дугу
29
Рис. 2.3
АА1 заменить хордой s, то можно с некоторой погрешностью определить среднюю скорость vср, которая по величине и по направлению отличается от скорости v.
vср s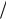 t .
t .
Переходя к пределу приt 0, т.е. приближая бесконечно точку А1 к точке А,
найдем истинную скорость Рис.2.4 материальной точки в положении А:
v lim |
s |
. |
|
|
(2.6) |
||
t 0 |
t |
||
При стремлении t к нулю направление vср в пределе совпадает с направлением касательной к дуге в точке А. Поэтому направление скорости материальной точки в любой момент времени совпадает с направлением касательной в этой точке, а величина ее равна пределу отношения приращения пути к приращению времени.
При неравномерном движении скорость изменяется по величине непрерывно, в каждый момент времени. Такую скорость можно измерить только в какое-то одно мгновение, поэтому ее называют мгновенной. Движение, при котором скорость возрастает, называют ускоренным, а приращение скорости за единицу времени – ускорением. Если скорость убывает, то – происходит замедление, ускорение при этом отрицательное.

30
Скорость и ускорение являются векторными величинами и с ними можно производить операцию геометрического сложения, как с векторами сил.
Пусть (рис. 2.5) материальная точка движется по дуге а – а с ускорением. В положении А скорость точки v, а в положении А1 скорость v1.
Перенесем вектор скорости v1 в точку А. Поскольку скорость точки постоянно растет, в положении А1 скорость точки больше, чем в положении А, поэтому учитывая, что скорость – векторная величина, запишем
v1 = v + v .
Из точки А по касательной к траектории а – а отложен вектор v, к концу которого
пристроен вектор v. Вектор v1 является замыкающим или суммирующим. Вектор приращения скорости v направлен под углом и к вектору v, и к вектору v1. Это говорит о том, что на участке АА1 происходит
изменение скорости как по величине, так и по направлению. Разложим вектор v на направление вектора v (составляющая тангенциальная vt) и направление радиуса дуги, перпендикулярного к вектору v (составляющая нормальная vn):
v = vt + vn ,
где vt - вектор тангенциального приращения скорости, которое увеличивает численное значение скорости v; vn – вектор нормального (радиального ) приращения скорости, которое изменяет направление скорости v, то есть поворачивает вектор от направления v до направления v1.
Ускорение точки – это отношение приращения скорости к приращению времени. Вектор среднего ускорения можно найти, если разделить вектор приращения скорости v на приращение времени t.
acp v t .
t .
