
1798
.pdf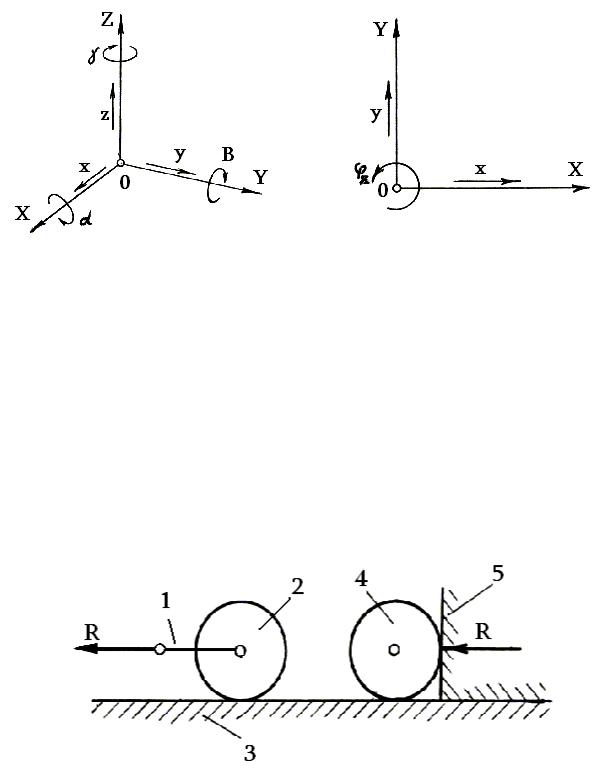
11
Рис.1.7 |
Рис 1.8 |
При взаимодействии между телом и связями возникают силы противодействия согласно аксиоме 4, которые препятствуют возможности движения тела. Тело действует на связи, т.е. преграды, а связи действуют на тело. Сила действия связи, т.е. преграды на тело, называется реакцией связи.
Связь ограничивает движение тела, поэтому реакция связи всегда направлена в сторону, противоположную тому движению, которому она препятствует.
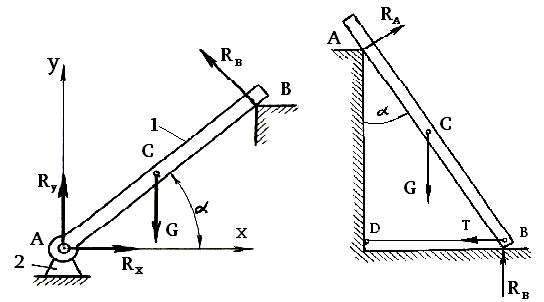
На рис. 1.9 нить 1 препятствует движению тела 2 и реакция связи R направлена противоположно движению. Тело 4 упирается в преграду (связь) 5, поэтому реакция R препятствует движению.
Определение реакций связей является одной из наиболее важных задач статики.
Рис. 1.9
В статике изучают несвободные неподвижные тела. Рассмотрим реакции различных связей.
Гибкие связи (рис. 1.10, а), осуществляемые нитями, канатами или тросами, удерживают тело А, не давая ему двигаться вниз под действием веса G. Реакции R гибких связей направлены вдоль нитей в

12
противоположную сторону, т.е. вверх. Нужно помнить, что гибкая связь может сопротивляться только растяжению (толкать нить не может, только тянуть).
Рис.1.10
На рис. 1.10, б изображено подъемное устройство. Блок 1 подвижный, к его оси подвешен груз G. Блок 2 неподвижный, его ось закреплена в кронштейне 3. Через блоки 1 и 2 переброшен канат 4, один конец которого закреплен в точке А, а за другой свободный конец в точке D его тянут вниз. При этом канат вращает блоки 1 и 2, блок 1 поднимается вверх, поднимая груз G. Трением каната о блоки пренебрегаем. Поскольку канатединое целое, то как любая нить он может иметь одну единственную растягивающую силу.
F = R , |
(1.2) |
где F – внешняя сила, приложенная к канату, а R – реакция нити. Если рассмотреть блок 1, то он вместе с грузом G удерживается двумя канатами (как в предыдущем примере). Реакция R гибких связей направлена вверх.
Три катка 5, 6 и 7 сложены штабелем на гладкой плоскости 8. Нижние катки 5 и 6, чтобы они не раскатились под весом верхнего катка 7, стянуты тросом AC. Вес трех катков воздействует на плоскость 8, которая согласно аксиоме 4 создает противодействие, т.е. реакции в точках касания катков 5 и 6.
Силы реакции в точках касания двух тел всегда направлены по нормали в точке касания. Нормалью к плоскости является перпендикуляр, восстановленный из точки касания. Нормалью к кривой является перпендикуляр, восстановленный из точки касания к касательной этой кривой.
На основании этого правила реакции R1 и R2 перпендикулярны к плоскости 8. Линии действия реакций R3 и R4 в точке касания катка 7 с катками 5 и 6 направлены по нормали и проходят через центры этих
13
катков. Реакции T троса AC направлены вдоль него и удерживают катки 5 и 6.
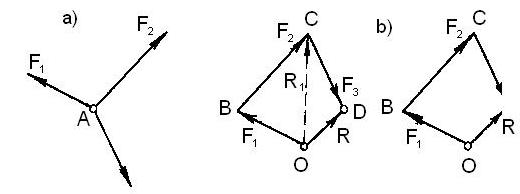
Рама 1 установлена шарнирно (рис.1.11) на кронштейне 2 и может поворачиваться вокруг оси А. Свободным концом рама опирается на опору в точке В. Вес рамы G приложен в ее центре тяжести C. Шарнир А у тела (рамы 1) отнимает две степени свободы X и Y, следовательно, в шарнире возникают две реакции Rx и Ry. В опоре B возникает реакция RB, которая направлена по нормали к поверхности, то есть перпендикулярно к плоскости рамы.
Балка, поставленная наклонно (рис. 1.12), нижним концом опирается на гладкий пол в точке B, а верхним - на стенку в точке A. В точке B балка нитью BD привязана к стенке в точке D. Вес балки G приложен в центре тяжести C. В точке А угол стены создает реакцию RA, которая перпендикулярна к балке. В точке B гладкий пол создает реакцию RB, перпендикулярную к полу. Нить BD создает реакцию T, которая удерживает балку от сползания по гладкому полу вправо.
Рис.1.11 |
Рис.1.12 |
Существование реакций обосновывается аксиомой 4 о действии и противодействии.
1.3. Плоская система сходящихся сил
1.3.1. Графический метод сложения сил
Система сил, линии действия которых пересекаются в одной точке, называют системой сходящихся сил. Другими словами – это система сил, приложенных к телу в одной точке.
14
Рис.1.13
Пусть дана система сил, приложенных к точке А (рис. 1.13, а). Для определения равнодействующей сил F1, F2, и F3 сложим последовательно попарно силы, используя правило треугольника. Сложим сначала силы F1 и F2 (рис. 1.13, б). Из произвольной точки О проведем вектор F1. Из конца вектора F1 (точка B) проведем вектор F2. Соединив точку О с концом вектора F2 ( точкой C), получим их равнодействующую R1, теперь сложим силу R1 с силой F3. Для этого из конца вектора R1 (точка C) проведем вектор F3, соединив точку О с концом вектора F3 (точка D), получим силу R, которая и есть равнодействующая заданных сил F1, F2 и F3.
Промежуточный вектор R1 можно не строить, а последовательно (рис. 1.13, в) в указанном выше порядке один вектор за другим откладывать все заданные силы, а начало первого вектора соединить с концом последнего. Это и будет равнодействующий вектор. Фигура OBCD называется силовым многоугольником. Замыкающая сторона силового многоугольника является равнодействующей системы сил. Равнодействующая R всегда направлена от начала первого вектора к концу последнего вектора. Другими словами, стрелка равнодействующей всегда направлена навстречу последовательного потока слагаемых векторов. Если при сложении сил вектор последней силы совместится с началом первой силы, то равнодействующая системы сходящихся сил будет равна нулю. В этом случае система сходящихся сил будет находиться в равновесии. Это и будет являться геометрическим условием равновесия системы сходящихся сил.
1.3.2. Проекция силы на оси координат
Многие задачи статики решают аналитическим методом, при котором используют не сами силы, а их проекции на оси координат.
Проекцией вектора на ось называется отрезок оси между основаниями перпендикуляров, опущенных из начала и конца вектора на ось.
15
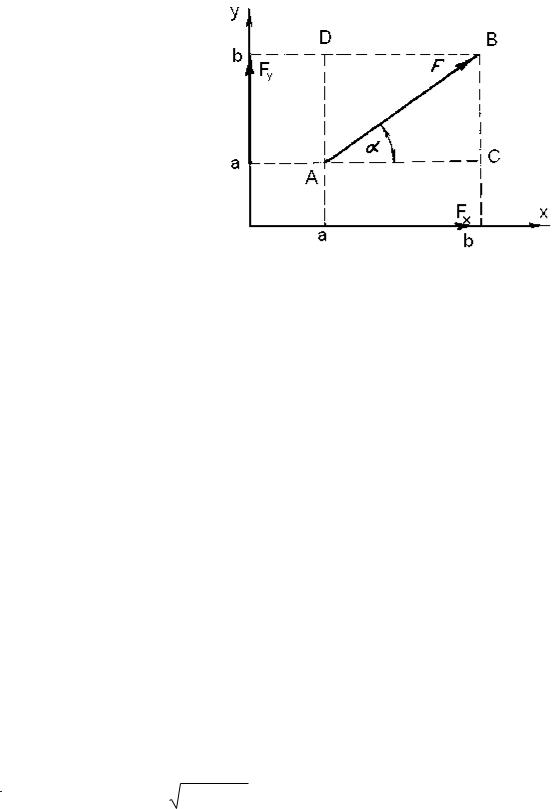
Например, проекцией вектора силы F на ось X будет отрезок ab оси X, где a и b есть основания перпендикуляров, опущенных из начала А и конца В вектора F. Проекцией силы F на ось Y будет отрезок а b оси Y.
Проекция вектора положительна, если она совпадает с направлением оси и, наоборот, отрицательна,
Рис.1.14
если направлена в сторону, противоположную оси. В приведенном примере на рис.1.14 обе проекции - положительны.
Чтобы найти величину проекции вектора силы F на ось X, опускаем перпендикуляры Aa и Bb (рис. 1.14) на эту ось. Длина проекции вектора определится из треугольника ABC:
Fx = ab = AC = F· cos . |
(1.3) |
Аналогично определяем величину проекции вектора силы F на ось Y:
Fy = а'b' = BC = F · sin . |
(1.4) |
Если сила F перпендикулярна оси X, то
Fx = F· cos900 |
= 0 ; |
(1.5) |
Fy = F · sin900 |
= F . |
Если сила F перпендикулярна оси Y, то
Fx = F · cos00 |
= F ; |
(1.6) |
Fy = F · sin00 |
= 0 . |
|
Если известна величина проекций силы F на оси X и Y, то применяя теорему Пифагора к треугольнику ABC, стороны которого равны векторам F, Fx и Fy, можно записать
F |
Fx2 Fy2, |
(1.7) |
где F – модуль (численное значение) вектора F; Fx – модуль вектора Fx; Fy – модуль вектора Fy.
16
1.3.3. Разложение сил на две составляющие
Рис.1.15
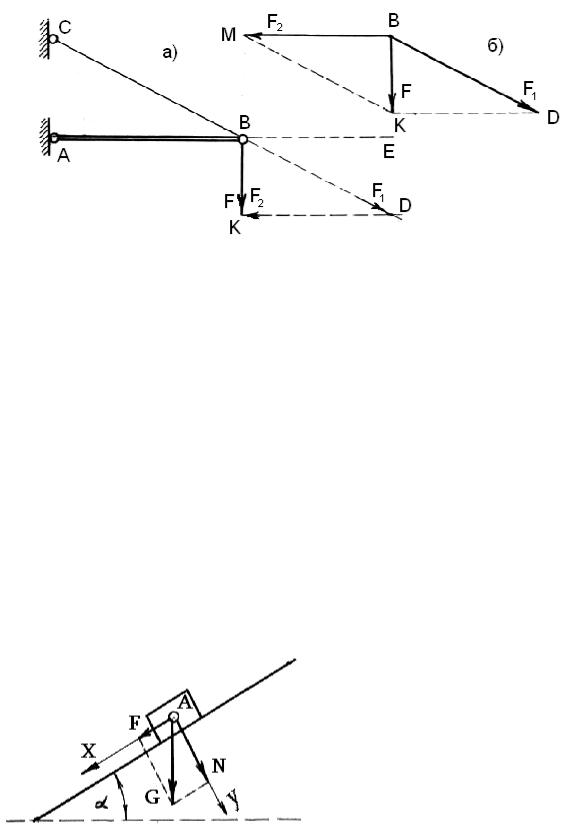
Зачастую при решении задач требуется одну силу F разложить на две составляющие. Например, требуется определить силу, которая растягивает нить BC (рис. 1.15, а), и силу, которая действует на стержень AB. Между стержнем и стеной установлен шарнир А. Стержень может воспринимать только силу, которая направлена вдоль его оси AB. Он может либо растягиваться, либо сжиматься. Итак, сила растягивающая нить, направлена вдоль BC в сторону BD, а сила действующая на стержень направлена вдоль AB. Задача сводится к тому, чтобы разложить силу F на две составляющие, параллельные AB и BC. Для этого из точки B (рис. 1.15, б) проводим вектор F. Из концов вектора F точек B и K проводим прямые BM, KD, BD и KM, которые параллельны AB и BC. В результате получим параллелограмм BDKM с диагональю BK. Из аксиомы 4 известно, что диагональю параллелограмма изображается равнодействующая сил, которые изображают стороны параллелограмма, т.е.
F = F1 + F2 . |
(1.8) |
Силы F1 и F2 приложены в точке B. Сила F1 растягивает нить BC, сила F2 сжимает стержень AB.
Применяя метод треугольника, из точки В (рис. 1.15, а) проводим продолжение линии CB, а из точки K проводим линию KD║ AB до пересечения с продолжением линии CB в точке D. Отрезок BD соответствует силе F1, отрезок KD соответствует силе F2.
Рис.1.16

17
Направление сил показано стрелками. При этом необходимо, чтобы равнодействующая F всегда была направлена от начала первого вектора F1 к концу второго вектора F2 .
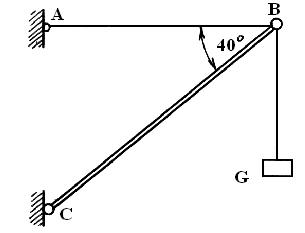
Разложение силы веса тела, лежащего на наклонной плоскости (рис. 1.16), на направление осей X и Y производится аналогичным образом.
Силы F и N построены на сторонах прямоугольника, диагональю которого является сила веса G.
1.3.4. Аналитический метод сложения сил
Рис. 1.17
Пусть дана система сходящихся сил F1; F2 и F3 (рис. 1.17, б), которые приложены к точке A. Требуется определить величину и направление равнодействующей аналитическим методом. Произведем вначале графическое сложение сил методом силового многоугольника. Из точки A (рис. 1.17, а) откладываем последовательно векторы F1; F2 и F3 методом их параллельного переноса с рис. 1.17, б. Получим разомкнутый многоугольник ACDB. Равнодействующая F является замыкающим отрезком AB этого многоугольника. Спроектируем все силы на ось X, которые будут изображаться отрезками:
F1x = ас; F2x = сd; F3x = db . |
(1.9) |
Сумму проекций можно представить в следующем виде:
n
Fix = F1x + F2x + F3x = -ac + cd + db = ab = Fx .
i 1
По аналогии для оси Y можно записать
n
Fiy = F1y + F2y + F3y = a′c′ + c′d′ – d′b′ = a′b′ = Fy .
i 1

18
Для упрощения обозначений в дальнейшем будем суммы проекций обозначать
n |
n |
|
Fix X |
и Fy Y . |
(1.10) |
i 1 |
i 1 |
|
Проекция векторной суммы на ось координат равна алгебраической сумме проекций слагаемых векторов на ту же ось и равна проекции равнодействующего вектора.
Итак, проекция равнодействующего вектора равна алгебраической сумме проекций всех сил, т.е.
Fx X ; |
Fy Y . |
(1.11) |
Модуль равнодействующей силы F через ее проекции (см. уравнение (1.7)) определяется по формуле
F |
F2 |
F2 . |
|
|
x |
y |
(1.12) |
|
|
|
|
Направление равнодействующего вектора, т.е. угол , определим, |
|||
пользуясь формулой (1.3): |
|
|
(1.13) |
cos =Fx/F ; |
sin =Fy/F . |
||
Если при сложении сходящихся сил равнодействующая будет равна нулю, то тело, к которому приложены силы, находится в покое. Это возможно, если
Fx X 0 ; |
Fy Y 0 ; |
F |
Fx2 Fy2 |
0 . |
(1.14) |
Таким образом, необходимым и достаточным условием равновесия плоской системы сходящихся сил является равенство нулю алгебраической суммы проекции всех сил на каждую координационную ось:
X 0 ; |
Y 0 . |
(1.15) |
Формулы (1.15) называют уравнениями равновесия плоской системы сходящихся сил и используют при аналитическом решении задач.
1.3.5. Примеры решения задач
Аналитический метод решения задач является универсальным и применяется чаще всего. Решение задач на равновесие плоской системы имеет следующую последовательность:
19
1.Выделяют тело или точку, где пересекаются линии действия сил, к этой точке прикладывают заданные силы.
2.Освобождают тело или точку от связей (принцип освобождаемости от связей) и заменяют их действие реакциями.
3.Выбирают координатные оси X и Y и относительно них составляют два уравнения равновесия (см. формулы (1.14)). Число неизвестных не должно быть более двух.
4.Решают систему уравнений (1.14) с двумя (или одним) неизвестными.
Линия действия реакций определяется сравнительно просто (см. §1.2). Нить имеет только одно направление. Опора (стена, пол, угол, другое тело и т.д.) тоже по закону противодействия имеет одно направление, а вот стержень, закрепленный по концам шарнирами, линию действия реакции имеет вдоль оси, но при этом он может как растягиваться, так и сжиматься. В этом случае направление реакции можно выбирать в ту или другую сторону. При определении модуля данной реакции может получиться знак плюс или минус. Если знак плюс, то направление реакции на схеме выбрано правильно. Если знак минус, то направление реакции нужно изменить на обратное и внести исправления в расчет и в схему.
Пример. Груз G = 5 кН подвешен на канате в точке B. Определить усилия в растяжке AB и стержне BC (рис. 1.18).
Ре ш е н и е
1.В точке B пересекутся линии действия заданной силы G
иискомых реакций в растяжке AB
истержне BC. Точку B выделяем как материальную точку, к которой приложены все силы.
Рис.1.18
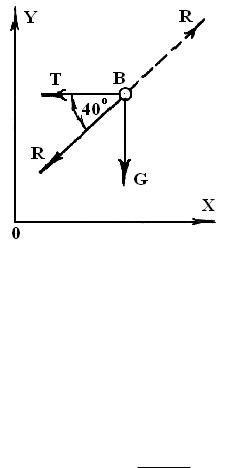
2.Освобождаем точку B от связей: растяжки AB и стержня BC и заменяем их реакциями T и R соответственно. Направление реакции R выбрано произвольно (рис. 1.19).
3.Выбираем координатные оси X и Y и составляем уравнение равновесия.
X T R cos 40 = 0 ;
20
Y G R sin 40 = 0.
Число неизвестных в двух уравнениях равно двум, поэтому уравнения эти решаются, а система является статически определимой.
4.Решаем систему уравнений. Из второго уравнения
R = - G/sin 40°= - 5/0.643 = -7.78 кН .
Подставив значение R в первое уравнение, получим
T = - R· cos 40° = 7,78· 0,766 = 5,96 кН .
Рис.1.19
Реакция R получилась с отрицательным знаком, поэтому нужно направление силы R исправить на обратное (пунктирное изображение). После этого уравнение перепишется в виде
X T R cos 40 = 0 ;
Y G R sin 40 .
и тогда
G |
|
T Rcos400 |
5,96кН . |
R sin400 |
7,78 кН ; |
Задачи на эту тему приводятся в задачнике [8, §2, с. 10 – 23].
1.4.Пара сил. Момент силы. Равновесие плоской системы сил
Две равные по величине параллельные силы, приложенные к телу и направленные в противоположные стороны, называются парой сил. Плоскость, в которой расположена пара, называют плоскостью действия пары сил. Сумма проекций пары сил на оси X и Y равна нулю:
X 0 ; Y 0 . (1.16)
Из этого можно сделать вывод: под действием пары сил тело не движется ни вдоль оси X, ни вдоль оси Y.
Пара сил характеризуется моментом, который вращает тело в плоскости XOY, то есть относительно оси Z, перпендикулярной плоскости
XOY. Момент пары сил относительно оси Z равен произведению |
|
Mz F a, |
(1.17) |
где F - одна из сил пары; а - плечо пары сил. |
|
