
1798
.pdf121
Q R |
A |
F R |
B |
F |
a |
. |
(11.13) |
|
|||||||
2 |
|
|
l |
|
|||
|
|
|
|
|
|
||
Знак поперечной силы |
– отрицательный. Откладываем |
на эпюре |
|||||
(рис.11.3,б) от оси 0-х ординату Q2=-RB на участке II и проводим прямую, параллельную оси 0=х. Получаем эпюру поперечных сил на участке II.
Вся эпюра поперечных сил представлена ступенчатой линией. Для I- го участка эпюра положительная, для II-го участка – отрицательная.
Запишем уравнение равновесия моментов относительно точки К2
откуда |
|
F(x2 - a) - RA x2 + Ми2 = 0, |
(11.14) |
||||
|
Ми2 = RA x2 - F(x2-a) |
(11.15) |
|||||
или |
|
||||||
|
|
|
|
b |
|
||
|
|
|
|
|
|
||
|
|
Ми2 |
F |
|
x2 F(x2 a). |
(11.16) |
|
|
|
|
|||||
|
|
|
ab |
|
l |
|
|
При х2=а; |
Ми2 |
F |
; при х2=l; Ми2=0. |
|
|||
l |
|
||||||
|
|
|
|
|
|
|
|
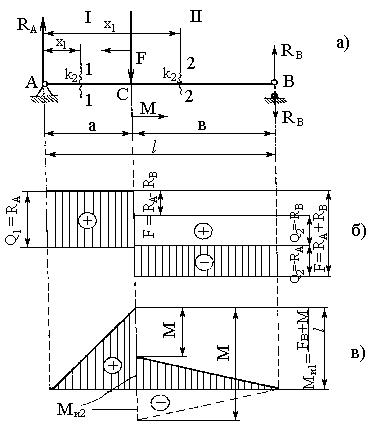
Координата х=а соответствует точке С. Здесь в конце участка I и начале участка II изгибающий момент Ми = Fab/l. В конце участка II, соответствующем точке В, изгибающий момент равен нулю. Соединяем эти точки прямой и получаем эпюру на участке II (рис.11.3,в).
Полная эпюра изгибающих моментов представляется треугольником, изгибающий момент во всех сечениях балки – положителен.
В сечении С, где приложена сила F, поперечная сила Q меняет свой знак, т.е. претерпевает разрыв на величину F, мгновенно переходя от +Q1 до -Q2.
Опасным сечением балки АВ будет точка С приложения силы F, где
Мmax = Fab/l и Qmax = RA= =Fb/l.
Построим эпюры для балки (рис.11.4,а), лежащей на двух опорах А и В и нагруженной силой F и парой сил с моментом М. Отбросим опоры А и В, заменив их реакциями RА и RВ. Составим уравнения равновесия. Приравняв нулю сумму моментов от внешних сил относительно точки А, получим
МА=М+RBl-Fa=0, |
|
||
откуда |
|
||
RB |
F a M |
. |
(11.17) |
|
|||
|
l |
|
|
Если Fa > M, то RB имеет знак (+). Если Fa < М, то RB имеет знак (-). Приравняв нулю сумму моментов от внешних сил относительно точки В, получим
МВ=М+F b-RAl=0,
122
откуда
F b M
RA |
|
. |
(11.18) |
|
l |
||||
|
|
|
Для проверки приравняем нулю сумму проекций всех сил на ось Y
Y=RA-F+RB=0, (11.19)
где знак силы RB.
Поперечная сила на участке I равна
|
|
|
Q R |
A |
|
Fb M |
. |
|
|
|
|
(11.20) |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
|
|
|
|
l |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Изгибающий момент на участке I равен |
|
|
|
|
|
|
|
||||||||||||
|
М |
u1 |
R |
A |
x |
Fb M |
x . |
|
|
|
|
(11.21) |
|||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
1 |
|
|
|
l |
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Fb M |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При х1=0; Ми1=0. При х1=а; |
|
Ми1 RAa |
|
|
|
a . |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
Поперечная |
сила |
|
на |
|
|
|
участке |
II |
с |
использованием |
|||||||||
уравнения (11.19) |
|
|
|
|
Q2 = RA - F . |
|
|
|
|
(11.22) |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
Если RA < F, то Q2 = -RB. Если RA > F, то Q = +RB. Решив уравнение |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.19) |
относительно |
F, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
получим |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
F = RA RB . |
(11.23) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знак реакции RB, как |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
указывалось |
выше, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
зависит |
от |
соотношения |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
внешнего |
момента М и |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
момента Fa. |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Построив |
эпюру |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
поперечных сил, |
получим |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
следующую картину: |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если Fa > M, то |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
реакция +RB положи- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
тельна, реакция RA < F, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
поперечная сила |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Q2 = RA - F = - RB; |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если Fa < M, то |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
реакция |
RB |
отрицательна |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(пунктирная |
стрелка), |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
реакция |
|
RA |
> |
F, |
||
|
Рис.11.4 |
|
|
|
|
|
|
|
|
|
|
|
поперечная сила |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
123
Q2 = RA - F = + RB (эпюра обозначена на рис. 11.4,б пунктирной линией). Изгибающий момент на участке II:
Ми2 = -М - F(x2 - a) + RA x2. (11.24)
Подставив значение RA из формулы (11.18), получит
|
|
|
|
Мu2 |
M F(x2 a) |
Fb M |
x2 . |
(11.25) |
||
|
|
|
|
|
||||||
|
При х2 = а |
|
|
|
|
l |
|
|||
|
|
|
Fb M |
|
|
|
|
|||
|
|
|
|
|
Мu2 |
a M . |
|
|||
|
|
|
|
|
|
|
||||
|
|
|
Fb M |
|
|
l |
|
|||
|
Если |
M |
, то изгибающий момент +Ми2 положителен. Если |
|||||||
|
l |
|||||||||
|
|
|||||||||
M |
Fb M |
, то изгибающий момент -Ми2 отрицателен. |
|
|||||||
l |
|
|||||||||
При х2 = l изгибающий момент, так как l - a = b,
Мu2 M Fb (Fb M)l 0. l
На рис. 11.4,б и 11.4,в приведены эпюры поперечных сил и изгибающих моментов.
11.3.Нормальные напряжения при изгибе
Впоперечных сечениях
балки кроме касательных (см. рис.11.1) возникают нормальные напряжения. При поперечном изгибе внутренние силы приводятся к поперечной силе Q и изгибающему моменту Ми.
Поперечная сила определяется касательными
напряжениями (см. рис.11.1,б), а |
|
||
изгибающий момент, как будет |
|
||
показано ниже, определяется |
|
||
нормальными напряжениями. |
|
||
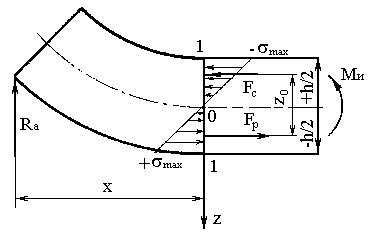
Вырежем |
из |
балки, |
|
испытывающей поперечный изгиб, |
|
||
участок длиной l=ОО (рис.11.5). |
|
||
Участок балки |
изгибается |
двумя |
|
изгибающими моментами Ми. |
Рис.11.5 |
||
124
При таком нагружении участок балки деформируется – изгибается выпуклостью вниз. Форма деформации показывает, что на выпуклой стороне материал растягивается (зона напряжения обозначена знаком +), а на вогнутой стороне материал сжимается ( зона сжатия обозначена знаком -). Между зонами растяжения и сжатия имеется нейтральный слой О-О. Продольные волокна на выпуклой стороне растянуты, на вогнутой стороне сжаты, а волокна нейтрального слоя О-О сохраняют первоначальную длину.
Рассмотрим растяжение волокна а-а, длину которого обозначим l1, а длину волокна О-О нейтрального слоя обозначим l. До деформации длина всех волокон равнялась длине волокна нейтрального слоя l. Удлинение волокна а-а равно l = l1-l, а относительное удлинение
|
|
l |
|
l2 |
l |
. |
|
|
|
|
|
|
|
|
|
(11.26) |
|||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
l |
l |
|
|
|
|
|
|
|
||||||||
Выразим длины дуг l и l1 через радиус и угол : |
|
|
|
|
|
||||||||||||||
l ; |
l1 z . |
|
|
|
|
|
|||||||||||||
Подставив значения l и l1 в уравнение (11.26), получим |
|
|
|
|
|||||||||||||||
|
z |
|
|
z |
. |
|
|
|
|
|
(11.27) |
||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Относительное удлинение материала при изгибе прямо |
|||||||||||||||||||
пропорционально расстоянию Z волокна от нейтрального слоя. |
|
|
|
||||||||||||||||
Если рассмотреть зону сжатия, то формула (11.27) примет вид |
|
|
|||||||||||||||||
|
( z) |
|
z |
. |
|
|
(11.28) |
||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Следствие. Наибольшее растяжение материала |
находится |
на выпуклой |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
поверхности |
|
балки, |
а |
||||||
|
|
|
|
|
|
|
|
|
|
сжатие |
– |
на |
вогнутой |
||||||
|
|
|
|
|
|
|
|
|
|
поверхности. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
результате |
удли- |
|||
|
|
|
|
|
|
|
|
|
|
нения и сжатия материала |
|||||||||
|
|
|
|
|
|
|
|
|
|
по |
|
обе |
стороны |
|
от |
||||
|
|
|
|
|
|
|
|
|
|
нейтрального |
слоя |
|
воз- |
||||||
|
|
|
|
|
|
|
|
|
|
никают |
внутренние |
силы, |
|||||||
|
|
|
|
|
|
|
|
|
|
которые противодействуют |
|||||||||
|
|
|
|
|
|
|
|
|
|
растяжению |
Fp |
и сжатию |
|||||||
|
|
|
|
|
|
|
|
|
|
Fc (рис.11.6). Они создают |
|||||||||
|
|
|
|
|
|
|
|
|
|
внутренний изгибающий |
|||||||||
Рис.11.6 |
|
|
|
|
момент Ми, который равен |
||||||||||||||
|
|
|
Ми = Fp Zo , |
|
|
|
|
(11.29) |
|||||||||||
125
где Fp = Fc – пара сил с плечом Zo, создающая изгибающий момент Ми, который уравновешивает внешний изгибающий момент (см. рис.11.1 и формулу (11.7))
Ми = Ra x.
Изогнутый стержень находится в напряженном состоянии. В каждой точке его поперечного сечения возникают нормальные напряжения , которые согласно закону Гука прямо пропорциональны относительному удлинению, т.е.
|
|
E E |
z |
. |
(11.30) |
|
|
|
|||
|
|
|
|
|
|
Из этого уравнения следует, что |
|
||||
нормальные напряжения в сечении 1- |
|
||||
1 (рис.11.6) изменяются по линейному |
|
||||
закону вдоль оси Z: когда Z = 0; =0, |
|
||||
когда Z = +h/2; |
= + max, когда Z = - |
|
|||
h/2; |
= - max. |
Знак (+) означает |
|
||
растяжение, знак (-) - сжатие. На рис. |
|
||||
11.6 изображена |
эпюра нормальных |
|
|||
напряжений по сечению балки. В |
|
||||
нейтральном слое |
напряжения равны |
|
|||
нулю, а к поверхности балки они |
|
||||
линейно возрастают до + max в нижнем |
|
||||
поверхностном слое и до - max в |
|
||||
верхнем поверхностном слое. |
Рис.11.7 |
||||
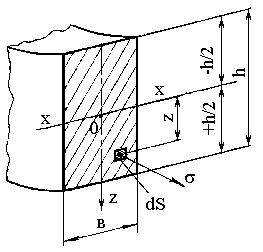
Определим величину изгибающего момента от внутренних сил. Элементарный момент от действия напряжения на элементарной площадке dS относительно оси х-х (рис.11.7) равен
dM dS z |
(11.31) |
||
Подставив значение из формулы (11.30), получим |
|
||
|
z2 |
|
|
dM E |
|
dS. |
(11.32) |
|
|||
|
|
|
|
Если проинтегрировать элементарные моменты по всей площади поперечного сечения S, то получим величину изгибающего момента
Мu dM |
E |
z |
2 |
dS . |
(11.33) |
|
|
||||
S |
S |
|
|
|
Сумма произведений (интеграл по площади S) элементарных площадок на квадрат их расстояния до нейтрального слоя х-х называется осевым моментом инерции

126
|
Ix z2dS . |
(11.34) |
|||||
|
|
|
S |
|
|||
Подставив уравнение (11.34) в (11.33), получим |
|
||||||
Мu |
|
E |
|
Ix |
|
||
|
|
||||||
|
|
|
|
|
|
||
или |
Мu |
|
|
||||
|
1 |
|
, |
(11.35) |
|||
|
|
|
|||||
|
|
EIx |
|
||||
где 1 называется кривизной (величина, обратная радиусу) |
балки, чем |
||||||
меньше , тем кривизна больше. Произведение EIх называется жесткостью сечения, которое характеризует сопротивление искривлению. С увеличением EIх кривизна уменьшается.
Если подставить значение 1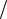 в уравнение (11.30), то получим
в уравнение (11.30), то получим
Ez |
Мu |
|
Мu z |
|
Мu |
. |
(11.36) |
EIx |
Ix |
|
|||||
|
|
|
Ix / z |
|
|||
Когда z = h/2, нормальное напряжение достигает максимума:
max |
hМu |
|
Мu |
. |
(11.37) |
2Ix |
|
||||
|
|
2Ix /h |
|
||
Отношение осевого момента инерции Ix к расстоянию до наиболее удаленных от нейтрального слоя волокон (h/2) симметричного сечения называется осевым моментом сопротивления и обозначается Wx:
Wx |
Ix |
. |
(11.38) |
|
|||
|
h/2 |
|
|
Этот момент сопротивления позволяет определить максимальное напряжение в материале изогнутого стержня
max |
Мu |
. |
(11.39) |
|
|||
|
Wx |
|
|
Момент сопротивления при изгибе играет такую же роль, как площадь поперечного сечения при растяжении и сжатии.
Вычислим значение момента сопротивления для простейших сечений.
Для валов круглого сечения осевой момент инерции равен
Ix |
d4 |
|
||
|
, |
(11.40) |
||
64 |
||||
|
|
|
||
осевой момент сопротивления ( h d )
2 2
127
Wx |
I |
x |
|
d |
4 |
|
d3 |
|
|
|
|
|
|
. |
(11.41) |
||||
|
|
|
|
32 |
|||||
|
h/2 |
64d /2 |
|
|
|||||
Для прямоугольного сечения (рис.11.7) осевой момент инерции
равен
bh3
Ix |
|
, |
(11.42) |
|
12 |
||||
|
|
|
осевой момент сопротивления
Wx |
I |
x |
|
bh3 |
2 |
|
bh |
2 |
. |
(11.43) |
|
|
|
12 |
|
h |
6 |
|
|||||
|
h/2 |
|
|
|
|
|
|||||
Для рационального использования материала форму поперечного сечения балок делают такого профиля, когда основная масса материала находится на возможно большем расстоянии от нейтрального слоя. Примером таких балок являются железнодорожные рельсы. В машиностроении и строительстве применяют балки таких профилей, как швеллер и двутавр. Геометрические характеристики таких сечений приводятся в справочной литературе.
11.4. Расчеты на прочность при изгибе
При изгибе балок сплошных поперечных сечений касательные напряжения по поперечному сечению не оказывают влияния на прочность. Поэтому прочность таких балок в условиях поперечного изгиба определяется максимальной величиной нормальных напряжений.
Опасное сечение балки находится максимальной величиной изгибающего момента. Для определения положения опасного сечения балки строится эпюра изгибающих моментов.
Проверка прочности и подбор сечений балок производится исходя из условия, чтобы наибольшие нормальные напряжения max не превосходили допускаемых [ ] на растяжение и сжатие для материала балки. Для балок из материалов, которые одинаково сопротивляются растяжению и сжатию (сталь, древесина), применяются симметричные сечения, чтобы максимальные растягивающие и сжимающие напряжения были равны
[+ max] = |
[- max]. |
|
|
|
|
Условие прочности имеет вид |
|
|
|||
|
max |
|
Mmax |
. |
(11.44) |
|
Wx |
||||
|
|
|
|
|
|
Это условие позволяет решать следующие три задачи.
1. Проверочный расчет или проверка прочности, когда известны размеры поперечного сечения балки, т.е. Wх, максимальный изгибающий момент, который будем для простоты расчетов впредь обозначать Ми, и

128
допускаемое напряжение [ ]. Напряжение max будем обозначать и. Для расчета используем условие (11.44), переписав его в виде
u |
|
Mu |
. |
(11.45) |
|
||||
|
|
Wx |
|
|
2. Проектный расчет или подбор сечения балки, когда известны внешние силы, определен наибольший изгибающий момент Ми=Мmax и известно допускаемое напряжение [ ]. Решив неравенство (11.45) относительно Wx, получим
Wx |
Mu |
|
. |
(11.46) |
Если сечение балки сложного профиля, то по таблицам, приведенным в справочниках, подбирают нужные размеры сечения, чтобы табличное значение Wx табл не превосходило расчетное значение Wx.
Если это вал круглого сечения, то подставив значение Wx из формулы (11.41) в формулу (11.46), получим
32Мu |
|
d 3 |
(11.47) |
. |
3. Расчет предельного изгибающего момента, когда для готовой конструкции требуется определить максимальную нагрузку. Решив неравенство (11.45) относительно Ми, получим значение предельного момента
Munp Wx . |
(11.48) |
Балку одинаковой длины, нагруженную одними и теми же внешними силами, можно изготовить:
1)из разных материалов ([ ] и [ ]);
2)с поперечным сечением разных размеров и разной формы (Wx1 и
Wx2).
Задача состоит в сравнении прочности этих балок. Критерием прочности выступает предельный момент Мипр. Если Мипр1 больше Мипр2, то балка 1 прочнее балки 2. Если предельные моменты у двух балок равны, т.е.
Мипр1 = Мипр2, |
(11.49) |
то такие балки называют равнопрочными. Подставив в равенство (11.49) значение моментов, получим
Wx1 1 Wx2 2 . |
(11.50) |
Если это вал круглого сечения, то подставив значение Wx из формулы (11.41), получим
d13 1 d23 2
32 32
129
или
d13 1 d23 2 .
Из этого уравнения можно получить различные вариации:
d |
3 |
|
|
|
|
|
d |
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
2 |
|
|
; |
1 |
3 |
|
|
|
; |
d d |
|
|
|
2 |
|
|
. |
||
d |
3 |
|
|
|
d2 |
|
|
1 |
2 |
|
|||||||||||||
2 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
||||
12.ИЗГИБ С КРУЧЕНИЕМ
12.1.Совместное действие изгиба и кручения
Валы одновременно с кручением испытывают изгиб под действием внешних сил и реакций опор. Разберем на примере совместное действие кручения и изгиба вала.
На рис. 12.1 изображен вал 3, установленный на опоры (подшипники) Н и К. На вал посажены шкивы 1 и 2, к которым в точках А и В приложены силы F1 и F2. Под действием этих сил вал находится в равновесии.
Перенесем силы F1 и F2 на ось х-
Рис.12.1
(11.51)
(11.52)
х в точки С и Е. В результате переноса получим: силу F1 (пунктирный вектор), приложенную в точке С, и момент крутящий Мк (пунктирный вектор), вращающий шкив 1 вокруг точки С; силу F2 (пунктирный вектор), приложенную в точке Е, и момент Мк (пунктирный вектор), вращающий шкив 2 вокруг точки Е. Так как вал находится в равновесии, крутящие моменты равны, поэтому можно записать
Mk F1 r1 F2 r2 . |
(12.1) |
Если в задаче задан крутящий момент, а силы не заданы, то их можно определить по формуле (12.1).
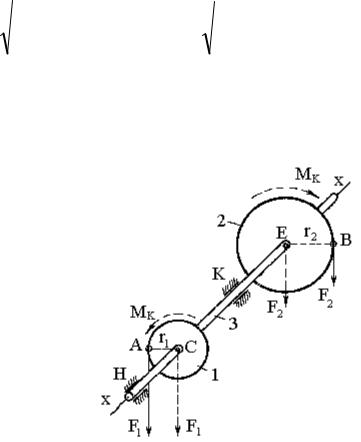
Составляем (рис.12.2) расчетную схему 1 (балка, нагруженная поперечными силами), определяем реакции опор Rн и Rк и строим эпюру изгибающих моментов Ми. Анализ эпюры показывает, что максимальный изгибающий момент Ми = Мmax находится в сечении под шкивом 1, т.е. в точке С, которая соответствует опасному сечению.
Составляем расчетную схему 2 и строим эпюру крутящих моментов
Мк.
130
При совместном действии изгиба и кручения в сечении вала (рис.12.3) возникают нормальные и касательные напряжения. Когда в каждой точке поперечного сечения действуют два разных напряжения ( и
), такое состояние материала называют сложным напряженным состоянием. Максимальные нормальные напряжения, возникающие от изгиба, расположены в волокнах, наиболее удаленных от нейтральной оси, определяются по формуле
u Mu 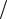 Wx .
Wx .
(12.2)
Максимальные касательные напряжения расположены на наружной поверхности вала и определяются по формуле
k Mk Wp .
Wp .
(12.3)
В этих формулах моменты сопротивления для круглого сплошного вала определяются по формулам:
осевой момент сопротивления
Wx |
d |
3 |
; |
(12.4) |
||
|
|
|
||||
32 |
|
|
|
|||
|
|
полярный момент сопротивления |
||||
Wp |
d |
3 |
. |
(12.5) |
||
|
|
|||||
16 |
|
|
|
|||
Из формул (12.4) и (12.5) видно, что Wp = 2Wx. Если обозначить момент сопротивления
Рис.12.2
W = Wx = Wp/2,
то тогда формулы (12.2) и (12.3) примут вид
u Mu  W . (12.6)
W . (12.6)
Максимальные касательные напряжения расположены на наружной поверхности вала и определяются по формуле
k Mk 2W . |
(12.7) |
Рис.12.3
