Задача 1.

Обезьяна за 2 часа срывает 64 кг бананов, а туземец за 3 часа – 72 кг. За сколько часов они нарвут 336 кг бананов?

Решение.

Определим, сколько бананов в час срывает каждый.

64 : 2 = 32 (кг) бананов в час – производительность труда

обезьяны.

72 : 3 = 24 (кг) бананов в час – производительность труда

туземца.

Их совместная производительность труда:

32 + 24 = 56 (кг) бананов в час.

Теперь определим искомое время:

336 : 56 6 (ч).

Ответ: за 6 часов.

Задача 2. Сергей может покрасить забор за 20 минут, а Егор – за 30 минут. За сколько минут, работая вместе, они могут покрасить забор?

Решение. Вся работа – это покраска забора. Площадь забора неизвестна, поэтому конкретно узнать производительность труда каждого (например, сколько кв. метров они покрасят за 1 минуту) нельзя. Значит, площадь всего забора мы примем за единицу площади, тогда производительность работы каждого будет выражаться дробью – частью забора, покрашенной за единицу времени.

Примем всю работу за 1, тогда за 1 минуту Сергей покрасит 1/20 часть забора, а Егор – 1/30 часть забора. Работая вместе, за минуту они покрасят 1/20 + 1/30 = 1/12 – это их совместная производительность труда. По формуле определим время, необходимое для совместной P покраски всего забора:

1/1/12 = 12 мин.

Задачи на смеси и сплавы

Теория

Предпосылки при решении задач на концентрацию

Концентрация вещества в растворе (смеси, сплаве) – это отношение массы или объема вещества к массе или объему всего раствора (смеси, сплава).

Например, если на флаконе написано, что это 5%-й раствор йода, значит на каждые 100 г раствора приходится 5 г йода, так как:

Как правило, концентрация выражается в процентах и обозначается буквой ω.

При решении задач на смеси и сплавы обычно принимают во внимание несколько правил-допущений.

Правило 1. Масса раствора или сплава равна сумме масс всех составляющих.

Например, если смешать 1,5 кг соли и 1 кг обычной воды, то получится раствор соли массой 1,5 + 1 = 2,5 кг.

Правило 2. При смешивании нескольких растворов (сплавлении нескольких кусков) получается новый раствор (новый сплав), являющийся суммой всех входящих в него растворов (сплавов).

Например, если сплавить куски массой 1,2 кг, 2 кг и 0,8 кг, то получится сплав весом 1,2 + 2 + 0,8 кг = 4 кг.

Правило 3. Массы растворенных веществ (металлов в сплавах) при смешивании (сплавлении) суммируются.

Например, если смешать 1 кг молока жирностью 6% (содержание жира 6% от 1 кг – т.е. 0,06 кг) и 2 кг молока жирностью 2% (содержание жира 2% от 2 кг – т.е. 0,04 кг), то получится 3 кг молока (1 кг + 2 кг) с содержанием жира 0,1 кг (0,06 кг + 0,04 кг).

Аналогичные правила действуют и на объемы веществ.

Проверь себя

11. Содержание серы в руде составляет 15%. Сколько серы содержится в куске руды массой 0,8 т?

12. Содержание воды в лимоне составляет 88%. Если лимон весит 120 г, сколько весит его сухое вещество (мякоть)?

13. Для приготовления раствора соды взяли 600 г воды и 150 г соды. Какова концентрация соды (по массе) в получившемся растворе?

14. 2 л 40%-го раствора этилового спирта разбавили 0,5 л воды. Чему равно содержание спирта в получившемся растворе? Ответ дайте в литрах.

15. Килограммовый слиток с 80%-м содержанием бронзы сплавили с таким же по массе слитком чистой бронзы. Чему равно содержание бронзы в полученном слитке? Ответ дайте в килограммах.

Основные типы задач на концентрацию

Все задачи, в которых фигурирует концентрация вещества, можно условно разделить на две группы. Рассмотрим типовые задачи в каждой из них и решим их алгебраическим способом.

4. Раствор или сплав смешивается с чистым веществом или водой

Необходимо помнить, что в чистой воде концентрация других веществ равна 0%. Аналогично, в чистом веществе концентрация этого вещества составляет 100% (так как предполагается, что других веществ и примесей там нет).

Пример. В колбу, содержащую 60 мл 40%-го раствора муравьиной кислоты лаборант долил 20 мл воды. Определите концентрацию муравьиной кислоты в полученном растворе.

Решение. Определим содержание кислоты в исходном растворе:

Содержание кислоты (по объему) в новом растворе не изменится (т.к. содержание кислоты в чистой воде равно 0%).

А вот объем раствора изменится и составит 60 + 20 = 80 мл.

Таким образом, концентрация кислоты в новом растворе составит:

Пример. В колбу, содержащую 30 мл 40%-го раствора муравьиной кислоты лаборант долил 10 мл обезвоженной (чистой) муравьиной кислоты. Определите концентрацию муравьиной кислоты в полученном растворе.

Решение. Вновь определим содержание кислоты в исходном растворе:

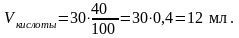
На этот раз содержание кислоты изменится – а именно, увеличится на 10 мл (т.к. в раствор добавляется 100%-ная кислота). На 10 мл увеличится и объем полученного раствора. В итоге, имеем следующую концентрацию кислоты:

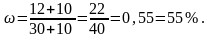
5. Смешивается несколько растворов (сплавляется несколько кусков металла) с разным содержанием входящих веществ

Покажем, как смешиваются вещества в растворах и сплавах.

Пример. Смешали 4 л 15%-ного раствора хлорида бария с 6 л 75%-ного раствора хлорида бария. Сколько процентов составляет концентрация хлорида бария в получившемся растворе?

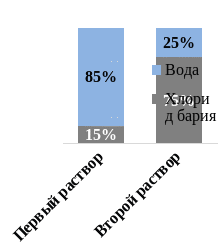Р ешение. Вычислим содержание каждого вещества в растворах.

Наглядно видно, что если смешать эти растворы, то всего хлорида бария в новом растворе будет 0,6 + 4,5 = 5,1 л. Если учесть, что при смешивании получилось 4 + 6 = 10 л раствора, то концентрация хлорида бария в новом растворе будет составлять:

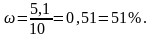
Иногда полезно обозначить искомую величину за х – и составить уравнение.

Пример. Сколько надо взять 5%-ного и 25%-ного раствора уксусной кислоты, чтобы получить 4 л 10%-ного раствора уксусной кислоты?

Решение. Пусть необходимо взять х л первого раствора. Тогда второго раствора необходимо взять (4 – х) л (т.к. всего должно получиться 4 л 10%-ного раствора).

В получившемся после смешивания растворе будет ровно столько уксусной кислоты, сколько ее было в каждом из взятых растворов. Поэтому выразим через переменную содержание уксусной кислоты в каждом растворе и приравняем к содержанию кислоты в итоговом растворе.

Получим следующее уравнение:

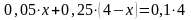
После упрощения получим:

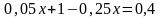
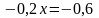
Таким образом, необходимо взять 3 л 5%-ного раствора кислоты и 1 л 25%-ного раствора кислоты.

Проверь себя

1. Имеется два равных по массе куска металла с содержанием хрома 54% и 68%. Чему будет равна концентрация хрома в сплаве, полученном из этих кусков?

2. Сколько литров воды нужно добавить в 2 л водного раствора, содержащего 60% кислоты, чтобы получить 20%-ный раствор кислоты?

3. Сплав меди и никеля (мельхиор) весом 600 г содержит 40% меди. Сколько граммов никеля нужно добавить, чтобы его концентрация в сплаве составила 80%?

4. К 15 л 10%-ного раствора щелочи добавили 10 л 5%-ный раствор щелочи. Определите концентрацию щелочи в получившемся растворе.

5. Смешали 4 л 15%-ного раствора соли с 5 л 20%-ного соли, после чего к смеси добавили 1 л чистой воды. Определите концентрацию полученной смеси.

Нестандартные методы решения задач на концентрацию

Большинство задач на концентрацию успешно решается с помощью таких методов как табличный метод и метод креста (конверта) Пирсона. Рассмотрим каждый из них подробнее.

1. Табличный метод

Пример. В колбу, содержащую 100 г 2%-ного раствора соли, добавили 175 г воды, некоторое количество соли и тщательно перемешали полученную смесь. Сколько граммов соли было добавлено, если известно, что после перемешивания получился 2,5%-ный раствор соли.

Решение. Обозначим неизвестное количество граммов соли за х и составим таблицу по условию задачи.

Для удобства в строках рекомендуется располагать все участвующие в процессе смешивания вещества и растворы по порядку их упоминания в задаче, а в столбцах – массу раствора, его концентрацию, а затем массу чистого вещества в растворе.

Распишем все данные в таблице подробно – в дальнейшем можно не составлять таблицу с подобным уровнем детализации.

	Масса раствора, г	Концентрация соли, %	Масса соли в растворе, г
Раствор	100	2% = 0,02	100 ∙ 0,02 = 2
Вода	175	0% = 0	175 ∙ 0 = 0
Соль	х	100% = 1	х ∙ 1 = х
Смесь	100 + 175 + х	2,5% = 0,025	(x + 275) ∙ 0,025

Составим уравнение по массе соли (сложим массы соли во всех смешиваемых веществах и растворах):

2 + 0 + х = (x + 275) ∙ 0,025

Отсюда х = 5.