Подготовка к огэ по математике Учебное пособие
9 Класс
Натуральные числа. Десятичная система счисления
Теория
Натуральные числа
Простейшие числа – это числа натуральные. Мы пользуемся ими в повседневной жизни для счета предметов, то есть для определения их количества и порядка.
Натуральные числа – это числа, используемые для счета предметов или для указания порядкового номера того или иного предмета среди однородных предметов.
Натуральные числа, расположенные в порядке возрастания, образуют числовой ряд. Он начинается с наименьшего натурального числа – 1. Наибольшего натурального числа нет, так как ряд натуральных чисел бесконечен. Если к любому натуральному числу прибавить единицу, то получаем число, следующее за данным числом.
Число 0 натуральным числом не является, так как означает полное отсутствие чего бы то ни было, значит, счет предметов тоже отсутствует.
Так же отрицательные и нецелые числа к натуральным не относятся.
Натуральные числа в общем виде обозначаются большой латинской буквой N.
Запись 5∈N значит, что число 5 принадлежит к натуральному ряду чисел. Запись –5∉N значит, что число –5 не принадлежит к натуральному ряду.
Например, из чисел 15; 2,5; –2,5; 0; 45; –45 выберите натуральные числа.
Рассмотрим каждое число по отдельности. Число 15 – целое и неотрицательное, может быть порядковым. 15∈N.
Число 2,5 – нецелое, следовательно, 2,5∉N.
Число –2,5 – нецелое и отрицательное, следовательно, –2,5 ∉N.
Число 0 натуральным числом не является, 0∉N.
Число 45 –целое и неотрицательное, может быть порядковым. Следовательно, 45∈N.
Число –45 – отрицательное. Следовательно –45∉N.
Ответ: 15 и 45.
Десятичная система счисления
Система счисления – метод записи чисел различными символами, представление чисел с помощью письменных знаков.
Выделяются многие различные системы счисления:
Двоичная – система счисления с основанием 2, для представления чисел в ней используются цифры от 0 до 1. Используется в программировании.
Восьмеричная – система счисления с основанием 8, для представления чисел в ней используются цифры от 0 до 7. Используется в программировании.
Десятичная – система счисления с основанием 10. Одна из наиболее распространённых систем. В ней используются цифры 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Целое число A в десятичной системе счисления записывается в виде конечной линейной комбинации степеней числа 10.
Также
число можно обозначить
.
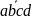Просто записать
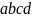нельзя, т.к. такая запись в соответствии
с принятыми в математике соглашением
означает произведение чисел a,
b,
c,
d.
Например,
.
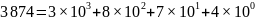Также существует римская система нумерации.
1 – I
2 – II
3 – III
4 – IV
5 – V
6 – VI
7 – VII
8 – VIII
9 – IX
10 – X
50 – L
100 – C
500 – D
1000 – M
Например, число MMMDCCLXIV представим арабскими цифрами.
MMM=3000
D=500
CC=200
L=50
X=10
IV=4
Получим 3000+500+200+50+10+4=3764.
Ответ: MMMDCCLXIV=3764.
Проверь себя
Из ряда: –4; –3,5; 0; 3,5; 4 выберите натуральные числа.
Представьте числа в виде конечной линейной комбинации степеней числа 10:
а) 327
б) 5214
в) 69013
г) 874139
д) 1756140
Числа, записанные в римской нумерации, представьте арабскими цифрами:
а) XIX
б) LXXII
в) CCCXIV
г) DCV
д) MCXI
е) MMMDCCCLXXXIX
Задания
Из ряда чисел выберите натуральные:
а) -1; 0; 1
б) 1; 2; 15
в) -10; -5; -8
г) 0; 0,1.
Представьте числа в виде конечной линейной комбинации степеней числа 10:
а) 0
б) 12
в) 327
г) 9 125
д) 15 997
е) 784 456.
Запишите число в римской нумерации:
а) 3
б) 25
в) 57
г) 129
д) 282
е) 624
ж) 1274
з) 5678.
Как из двух спичек сложить «пять»?
Сложите из спичек равенство: IX + VI = XI. Переложите одну спичку так, чтобы получилось верное равенство.