3, 4 Кинематика вращательного движения. Связь между линейными и угловыми ускорениями.

Вращательным движением называется такое движение, при котором траектории всех точек тела являются концентрическими окружностями, центры которых лежат на одной неподвижной прямой, называемой осью вращения.

Любое сложное движение твердого тела состоит из простых движений: поступательного и вращательного. Вращение вокруг неподвижной оси

Пусть твердое тело, вращаясь вокруг неподвижной в данной системе отсчета оси совершило за время бесконечно малый поворот (рис. 2.2). Соответствующий угол поворота будем характеризовать вектором , модуль которого равен углу поворота, а направление совпадает с осью , причем так, что направление поворота отвечает правилу правого винта (буравчика) по отношению к направлению вектора .

Теперь найдем элементарное перемещение любой точки твердого тела при таком повороте. Положение точки зададим радиус-вектором , проведенным из некоторой точки на оси вращения. Тогда линейное перемещение конца радиус-вектора (рис. 1.1) связано с углом поворота соотношением или в векторном виде . (2.1) Отметим, что это равенство справедливо лишь для бесконечно малого поворота . Кроме того, введенный нами вектор удовлетворяет основному свойству векторов – векторному сложению (это можно доказать). Заметим, что при рассмотрении таких величин как радиус-вектор , скорость , ускорение , не возникал вопрос о выборе их направления: оно вытекало естественным образом из природы самих величин. Подобные векторы называют полярными. В отличие от них векторы типа , направление которых связывают с направлением вращения, называют аксиальными, или псевдовекторами. Введем векторы угловой скорости и углового ускорения. Вектор угловой скорости определяют как , (2.2) где – промежуток времени, за который тело совершает поворот . Вектор совпадает по направлению с вектором и представляет собой аксиальный вектор. Изменение вектора со временем характеризуют вектором углового ускорения , который определяют как Направление вектора совпадает с направлением – приращения вектора . Вектор , как и , является аксиальным. Единицей угловой скорости в «СИ» является радиан в секунду (с^-1), а единицей углового ускорения – радиан на секунду в квадрате (с^-2).

В проекциях на ось вращения , положительное направление которого свяжем с положительным направлением отсчета координаты – угла поворота – правилом правого винта (рис. 2.3).

Тогда проекции и векторов и определятся формулами (2.4) Здесь и – величины алгебраические. Их знак характеризует направление соответствующего вектора. Например, если , то направление вектора совпадает с положительным направлением оси ; если же , то направление вектора противоположно. Аналогично и для углового ускорения.

Связь между линейными и угловыми скоростями.

Найдем скорость производной точки твердого тела, вращающегося вокруг неподвижной оси с угловой скоростью . Пусть положение точки относительно некоторой точки оси вращение характеризуется радиус-вектором (рис. 2.4.).

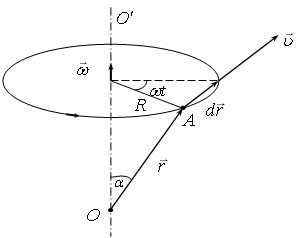
Записав и поделив ее на соответствующий промежуток времени , получим

; , то то есть скорость любой точки твердого тела, вращающегося вокруг некоторой оси с угловой скоростью , равна векторному произведению на радиус-вектор точки относительно произвольной точки оси вращения.

Модуль вектора где – радиус окружности, по которой движется точка . Продифференцировав (2.6) по времени, найдем полное ускорение точки :

. (2.7)

В данном случае (ось вращения неподвижна) , поэтому вектор представляет собой тангенциальное ускорение . Вектор же – нормальное . Модули этих ускорений Отсюда модуль полного ускорения .

Связь между линейным и угловым ускорением

Чтобы найти связь между модулями линейного (тангенциального) и углового ускорений, продифференцируем формулу

Получим

Из формулы следует, что линейное (тангенциальное) ускорение равно угловому, умноженному на радиус.