1.Кинематика поступательного движения. Вектор скорости и ускорения.

Поступательное движение твердого тела. Аналогии между формулами вращательного и поступательного движений. При поступательном движ все точки тела получают за промежуток времени одинаковое перемещение. Поэтому достаточно определить движение одной из точек тел, например центра масс, что бы охарактеризовать всё движение в целом. При вращательном движении все точки движутся по окружности, центры которых лежат на одной и той же прямой, назыв осью вращения. Аналогии – 1)Поступательное-2)Вращательное: 1-1)Закон сохранения импульса: 1-2)Закон сохранения момента импульса . 2-1) 2й Закон Ньютона: 2-2)Основное уравн динамики вращ движ I .3-1)Кинетическая энерг: . 3-2)Вращ движение: . 4)-Выражение для элементарной работы : 1) 2)

Угловая скорость и ускорение. Угловой скоростью называется вектор­ная величина, равная первой производной угла поворота тела по времени: Размерность угловой скорости dim=T^-1, a . ее единица — радиан в секунду (рад/с).Линейная скорость точки

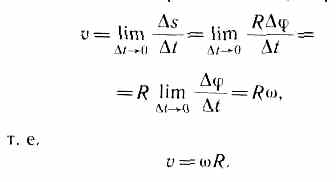
В векторном виде Угловым ускорением называется век­торная величина, равная первой производ­ной угловой скорости по времени:

2 Средние значения. Вычисления пройденного пути

Путь(s) - часть траектории, совершаемая объектом. Весь путь s, пройденный частицей можно представить как сумму путей

,

пройденных за соответствующий промежутки времени ∆t.

Скорость – векторная физическая величина, определяющая как быстроту движения, так и направление движения в данный момент времени.

Рассмотрим общий случай неравномерного криволинейного движения.

Пусть в момент времени движущееся точечное тело занимает положение, характеризующееся радиус-вектором или координатами . К моменту времени тело займет новое положение с и координатами . За отрезок времени , координаты движущегося тела изменяются на

а приращение радиус-вектора за это время будет равным: проекции на оси координат будут

или вектор выразиться через свои проекции следующим образом ,где – орты. Величина вектора будет равна . вектор , направленный из начального положения в конечное положение , движущегося в течение времени точечного тела, называется вектором перемещения. Расстояние между и , отсчитанное вдоль траектории, называется путем , пройденным точкой. Путь – скалярная величина.

В общем случае криволинейного движения вектор не совпадает с участком траектории , проходимым телом за соответствующий отрезок времени. В криволинейном движении . Из того, что перемещение – вектор, следует подтверждающийся на опыте закон независимости движений: если точка одновременно участвует в нескольких движениях, то результирующее перемещение точки равно векторной сумме перемещений, совершаемых ею за то же время в каждом из движений порознь. Если за время радиус-вектор движущейся материальной точки изменяется на , то среднее его изменение за 1 единицу времени будет . величина , равная среднему изменению радиус-вектора материальной точки за единицу времени, называется средней скоростью ее перемещения за время между и .Она является величиной векторной, так как получается делением вектора на скаляр . Направление средней скорости совпадает с направлением хорды 1,2, то есть с .В случае неравномерного движения с изменением отклонение будет изменяться, то есть .

При движении материальной точки по прямой в одном направлении пройденный путь и модули вектора перемещения совпадают .

Средней скоростью прохождения пути неравномерного движения материальной точки на данном участке ее траектории называется скалярная величина, равная отношению длины пути ко времени , за которое этот путь пройден.

Величину истинной скорости (без учета направления) можно определить таким образом. При длина вектора перемещения в пределе совпадает с элементом пути , так что . С учетом этого величина скорости может быть представлена в виде

, , то есть величина скорости есть производная пути по времени.

Если дана графическая зависимость проходимого телом пути от времени , то величина скорости в данный момент времени будет равна наклона касательной, проведенной в точке кривой , соответствующей этому моменту времени и оси времени Зная модуль скорости в каждый момент времени, можно вычислить путь, пройденный частицей от до ,где .

Величиной, характеризующей быстроту изменения скорости с течением времени, является ускорение. Пусть в момент времени скорость движущегося тела , а в момент времени - . За отрезок времени скорость изменилась на . В среднем за единицу времени изменение скорости будет равно – среднее ускорение движения тела.