§11. Релятивістська динаміка.

Для знаходження рівняння руху матеріальної точки, на яку діє сила (основного закону динаміки СТВ), необхідно:

1) шукати (постулювати) його в чотиривимірній формі (див. зауваження наприкінці §10);

2) задовольняти при цьому принципу відповідності з динамікою Ньютона, тобто при з чотиривимірного закону динаміки повинний випливати другий закон Ньютона:

, (11.1)

Тому ми повинні попередньо визначити чотирьохвектор імпульсу і чотирьохвектор сили як природне 4-мірне узагальнення векторів і .

Чотирьохвектор імпульсу р^ визначений формулою:

, , (11.2)

де m₀ – так називана маса спокою (тобто маса матеріальної точки що покоїться). Компоненти р^ мають вигляд:

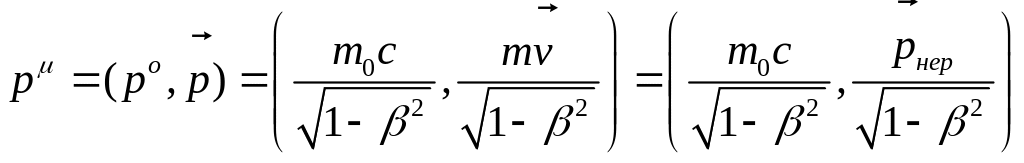(11.3)

Тривимірний вектор:

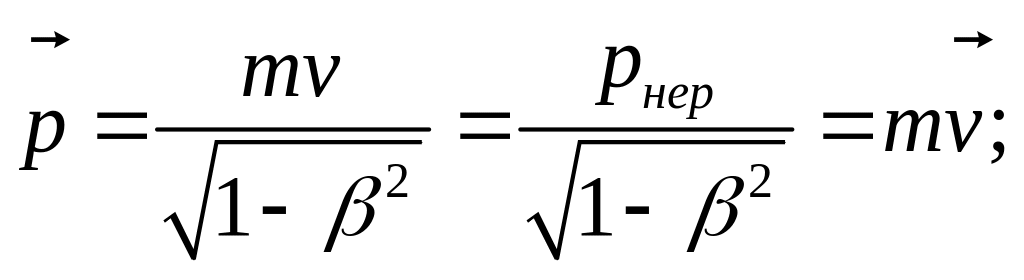
(11.4)

називається релятивістським імпульсом. З (11.4) видно, що (як і нерелятивістський імпульс ) його можна представити як величину, пропорційну швидкості, якщо масу m матеріальної точки, що рухається, визначити співвідношенням:

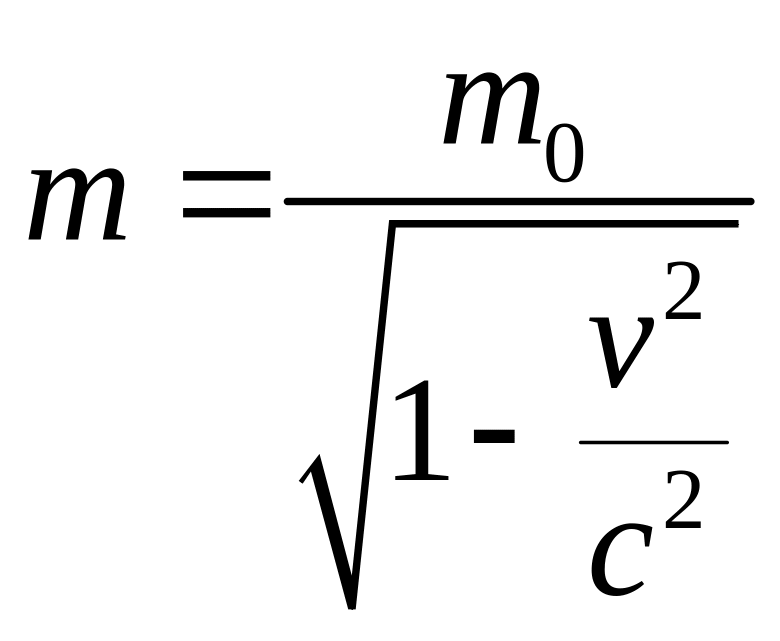(11.5)

тобто маса частки (тіла) росте зі збільшенням її швидкості. Це означає, що СТВ маса m залежить від вибору ІСВ, тобто не є абсолютною величиною (на противагу класичній механіці, де , тобто маса не залежить від вибору ІСВ). При малих швидкостях ( ) вираз (11.4) для релятивістського імпульсу переходить у визначення нерелятивістського імпульсу.

Вводячи тепер для чотирьохвектора сили (сили Минковского) позначення , постулюємо шуканий основний закон динаміки СТВ (4-мірне рівняння руху) у вигляді:

(11.6)

У компонентному вигляді ці чотири рівняння можна записати так:

(11.7)

(11.8)

З'ясуємо тепер зв'язок з звичайним вектором сили . Для цього перепишемо (11.8) у вигляді (з огляду на, що ):

(11.8^/)

Щоб задовольнити принципу відповідності з рівнянням (11.1) ми повинні прирівняти праву частину (11.8^/) вектору , тобто покласти:

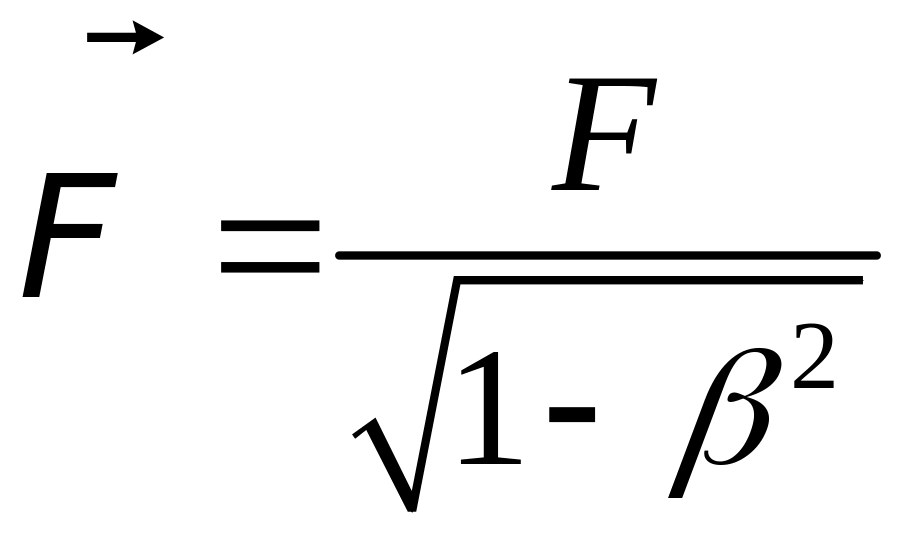(11.9)

Таким чином, вектор зв'язаний зі звичайною силою співвідношенням (11.9), тому (11.8) можна записати у вигляді:

(11.8^//)

де дається вираженням (11.4). Рівняння (11.8^//) є релятивістська форма запису другого закону Ньютона: це рівняння коректно описує динаміку релятивістської (тобто, що рухається з будь-якими швидкостями в інтервалі ) матеріальної точки в заданій ІСВ. Це рівняння тривимірне, тому неінваріантне щодо перетворень Лоренца.

Далі, підставляючи (11.2) у (11.6), перепишемо основний закон руху динаміки СТВ у вигляді:

(11.6^/)

де - чотирьохвектор прискорення (10, …)...Підставляючи (11.6^/) у співвідношення (10, …), маємо:

,

звідкіля, з огляду на (10,…)і (11.9), одержуємо для компонента вираз:

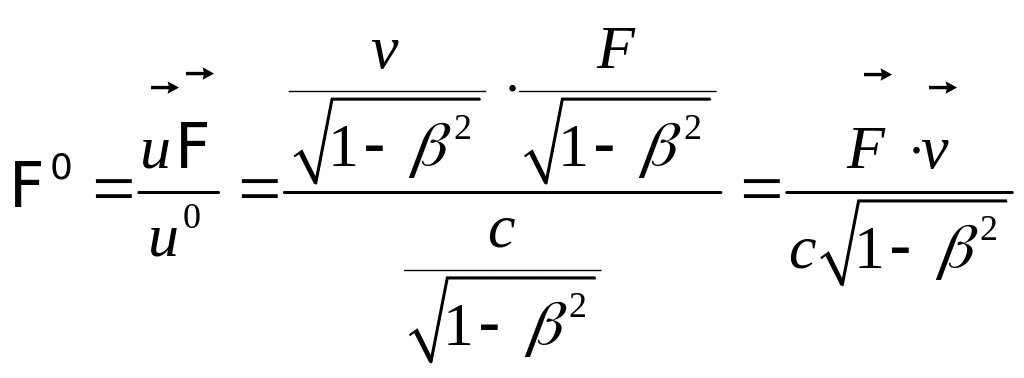, (11.10)

тобто компонент зв'язаний з механічною потужністю (роботою в одиницю часу). Таким чином, вираз (11.9) і (11.10) дозволяє записати компоненти сили Минковского у вигляді:

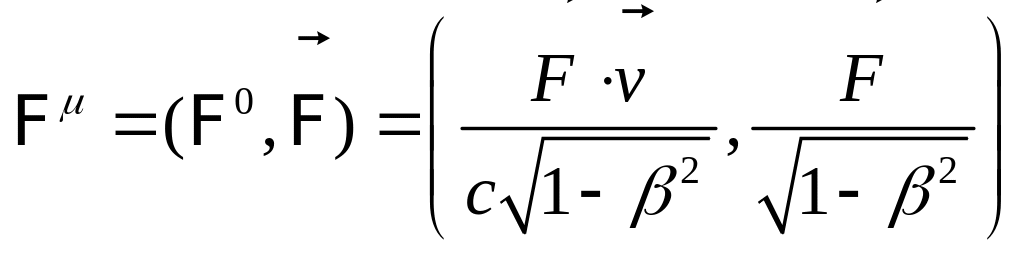(11.11)

З'ясувавши фізичний зміст компонентів чотирьохвектора сили і рівняння (11.8), перейдемо до з'ясування фізичного змісту рівняння (11.7). Приймаючи до уваги формули (11.3) і (11.10), перепишемо (11.7) у вигляді:

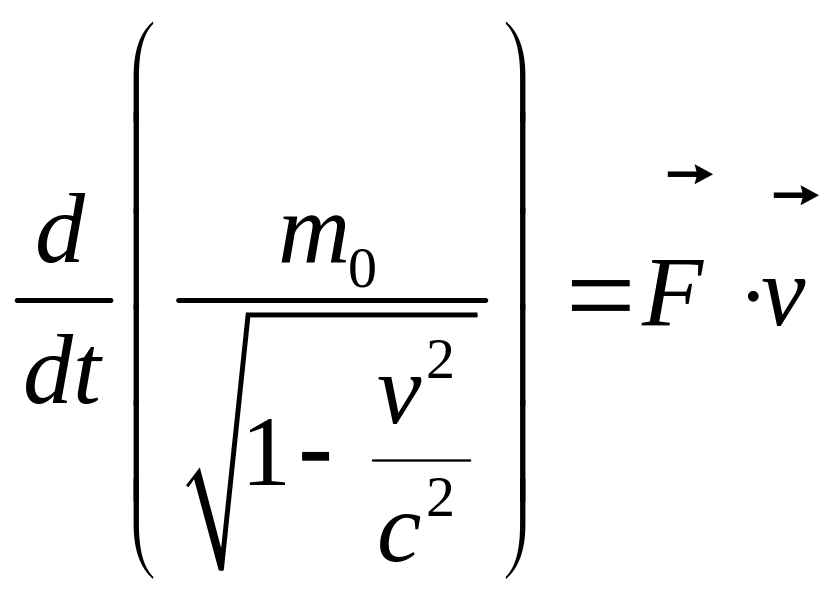(11.7^/)

Так праворуч у (11.7^/) стоїть вираз для роботи в одиницю часу, що виконує сила , тобто ґрунтуючись на законі збереження і перетворення енергії (який виконується в СТВ в силу однорідності часу), ми можемо стверджувати, що ліворуч у рівності (11.7^/) стоїть вираз для зміни енергії матеріальної точки в одиницю часу. Отже, у дужках у лівій частині (11.7^/) стоїть вираз для енергії матеріальної точки, визначений з точністю до довільної постійної (можна однак показати, що ця постійна повинна бути обрана рівної нулю – у протилежному випадку буде протиріччя з законом додавання швидкостей у СТВ). У такий спосіб величина:

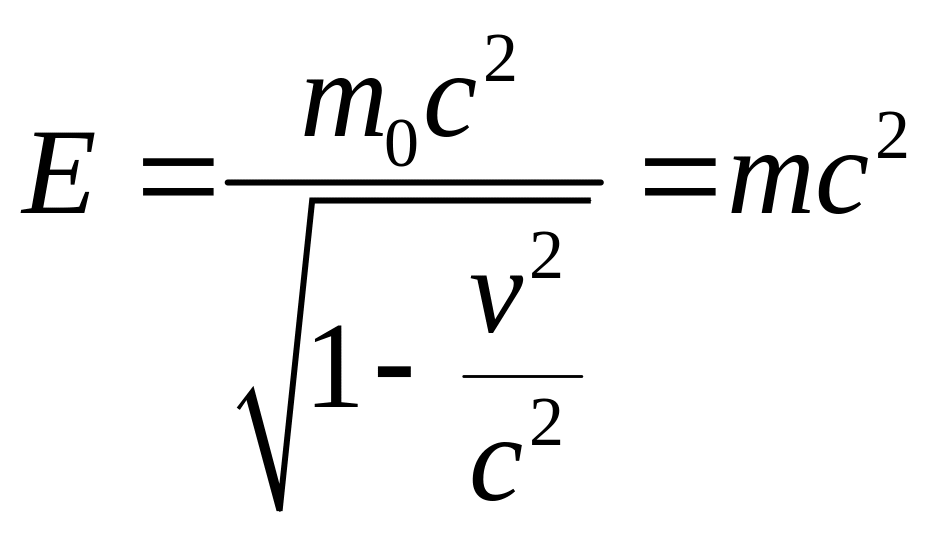(11.12)

визначає енергію матеріальної точки (тіла), що рухається зі швидкістю v. При v=0 з (11.12) одержуємо:

(11.13)

так звану енергію спокою матеріальної точки (тобто її внутрішню енергію). Таким чином, з масою завжди зв'язана енергія (і навпаки), тому в релятивістській механіці не існує окремо законів збереження маси й енергії – вони поєднанні в єдиний закон збереження повної (тобто, що включає енергію спокою) енергії частки. Наближений їхній поділ можливий лише в класичній фізиці, коли і не відбувається перетворення одних часток в інші: при з (11.12) маємо:

(11.14)

При енергія масивної частки, згідно (11.12) збільшується нескінченно. Тому, приймаючи до уваги закон збереження енергії, дійдемо висновку: прискорити масивне тіло до неможливо, тому що для цього треба була б нескінченна енергія, що, в принципі, не здійсненно. Зі швидкістю світла у вакуумі можуть рухатися тільки "безмасові" тіла, для яких m₀ = 0 (наприклад, фотони).

З врахуванням (11.12), компоненти чотирьохвектора імпульсу р^ (11.3) можна представити у вигляді:

(11.15)

Тому вираз для квадрата 4-вектора імпульсу можна переписати так:

(11.16)

Співвідношення між енергією і релятивістським імпульсом (11.6) широко використовується в сучасній фізиці (нагадаємо, що в класичній механіці відповідне співвідношення мало вигляд ). Для часток з нульовою масою спокою з (11.16) випливає:

( 11.17)

Для вільної матеріальної точки замість (11.6) маємо:

чи (11.18)

тобто збереження 4-вектора імпульсу, що згідно (11.15) означає одночасне збереження й енергії ( ) і релятивістського імпульсу ( ).

Зауваження. У цьому параграфі ми побудували релятивістську динаміку однієї матеріальної точки, що рухається в деякім силовому полі. Шляхом очевидних узагальнень легко побудувати динаміку системи, що складається з багатьох матеріальних точок за умови, що ці точки між собою не взаємодіють. Для таких систем їхні повні характеристики, такі як повна енергія системи Е, релятивістський імпульс системи, чотирьохвектор імпульсу системи р^, є аддитивними величинами:

, , ,

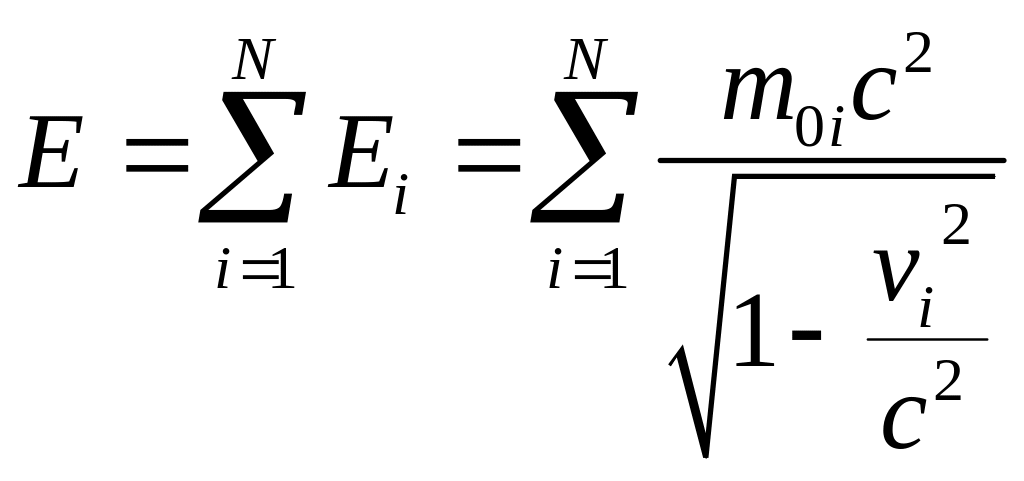Однак при врахуванні взаємодії між матеріальними точками ситуація різко ускладнюється, тому що всі перераховані величини втрачають властивості аддитивності. Це зв'язано c тією обставиною, що при утворенні з вільних часток стійкої системи взаємодіючих часток виділяється надлишок енергії (рівний енергії зв'язку) Е, якому згідно (11.12) відповідає маса . . Тому повна маса системи менше суми мас її часток, що утворяться, на величину (так званий дефект мас), і згадані властивості аддитивності губляться. Унаслідок цього проблема побудови релятивістської динаміки систем взаємодіючих часток виявляється дуже складною і відповідної теорії в даний час не існує (маються тільки деякі наближені результати для випадку слабкої взаємодії між класичними частками).

Розділ 3. Релятивістська інваріантість законів електродинаміки вакууму.

У цій главі ми переконаємося в релятивістській інваріантності законів електродинаміки для зарядів і струмів у вакуумі (рівняння для електромагнітних потенціалів і рівнянь Максвела). Для цього, як ми покажемо в §12, необхідно записати ці закони в чотиривимірній формі, тобто у вигляді тензорних рівнянь у П-Ч Минковского.