2.3.3. Форматы двоично-десятичных чисел

Такие числа могут быть представлены в двух форматах: зонном и упакованном. В этих форматах каждая десятичная цифра и знак числа заменяются двоичной тетрадой в соответствии с используемым двоично-десятичным кодом. Количество цифр в числе может быть произвольным.

В зонном формате под каждую десятичную цифру отводится байт (рис. 2.8). В старшей тетраде записывается код зоны (например, код 1111), а в младшей – код цифры. В младшем байте вместо кода зоны записывается знак числа.

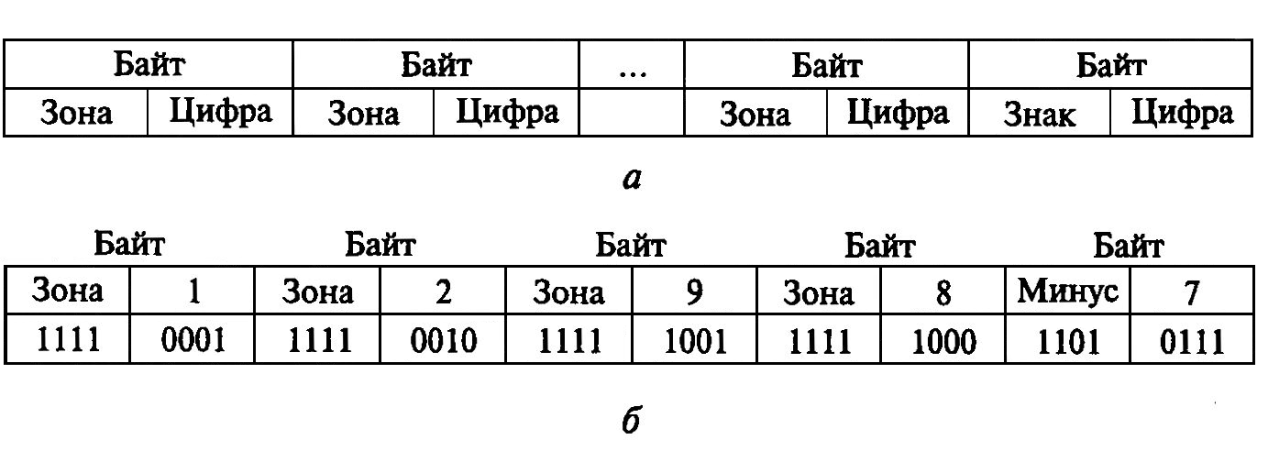
Рис. 2.8. Зонный формат двоично-десятичных чисел:

а – структура формата; б – пример записи числа -12987

В упакованном формате байт содержит две цифры (рис. 2.9). Младшая тетрада последнего байта содержит знак числа.

Байт		Байт		…	Байт		Байт
Цифра	Цифра	Цифра	Цифра		Цифра	Цифра	Цифра	Знак

а

Байт		Байт		Байт		Байт
0	2	3	7	4	6	5	Плюс
0000	0010	0011	0111	0100	0110	0101	1100

б

Рис. 2.9. Упакованный формат двоично-десятичных чисел:

а – структура формата; б – пример записи числа +237465

Пример 2.1. Записать число -12,25 в формате с плавающей точкой.

Решение.

1. Переводим абсолютную величину числа в двоичную систему счисления:

–12,25₁₀ = 12,25₁₀ = 1100,010₂.

2. Нормализуем до 1:

.

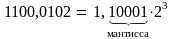Степень двойки есть абсолютный порядок.

3. Вычисляем смещенный порядок. Смещенный порядок = абсолютный порядок равен + 127

3 + 127 = 130.

130₁₀ = 10000010₂.

4. Если знак числа равен 1, то число отрицательное, если 0 – положительное

5. Заполняем 32-разрядную сетку:

1	1	0	0	0	0	0	1	0	1		0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Знак числа	Смещенный порядок									Мантисса без первой 1

Пример 2.2. Значение переменной A представлено в формате с плавающей точкой в шестнадцатеричной системе A = 430F0000₁₆. Найти значение числа A в десятичной системе счисления.

Решение.

Переходим от шестнадцатеричной системы счисления к двоичной системе счисления. Число занимает в памяти машины 32 бита

430F0000₁₆ = 0100 0011 0000 1111 0000 0000 0000 0000₂.

0	1	0	0	0	0	1	1	0		0	0	0	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
знак мантиссы	Смещенный порядок								Мантисса без первой 1

Находим абсолютный порядок

10000110₂ = 134₁₀.

134 – 127 = 7 – абсолютный порядок

Записываем мантиссу – первая единица будет всегда + 7 разрядов в поле «Мантисса без первой 1».

+1.00011110000₂  2⁷ = + 10001111 = 71.

Ответ: 71₁₀.