
- •Раздел 2 принципы построения и функционирования эвм и вычислительных систем (вс)
- •2.1. Структура эвм
- •2.2. Системы счисления
- •2.3. Формы представления чисел
- •2.3.1. Форма представления чисел с фиксированной точкой
- •2.3.2. Форма представления чисел с плавающей точкой
- •2.3.3. Форматы двоично-десятичных чисел
- •2.3. Машинные коды
- •2.3.1. Прямой код
- •2.3.2. Обратный код
- •2.3.3. Дополнительный код
- •2.4. Перевод чисел из одной системы представления в другую
- •2.4.1. Перевод между основаниями, составляющими степень двойки
- •2.4.2. Перевод целого числа из десятичного счисления в другое
- •2.4.3. Перевод дробного числа из десятичного счисления в другое
- •2.4.4. Перевод чисел в десятичную систему счисления
- •2.5. Арифметические действия над двоичными числами
- •2.5.1. Сложение
- •2.5.2. Вычитание
- •2.5.3. Умножение
- •2.5.4. Деление
- •2.6. Понятие алгебры логики
- •2.7. Простейшие логические функции
- •2.7.1. Логическая операция конъюнкция (логическое умножение)
- •2.7.2. Логическая операция дизъюнкция (логическое сложение)
- •2.7.3. Логическая операция инверсия (отрицание)
- •2.7.4. Логическая операция сложение по модулю 2
- •2.7.5. Логическая операция эквивалентность (функция тождества)
- •2.7.6. Логическая операция импликация (логическое следование)
- •2.7.7. Функция Шеффера
- •2.7.8. Стрелка Пирса ав, или функция Вебба a b
- •2.8. Основные правила преобразования формул
- •2.9. Кодирование текстовой информации
- •2.10. Составные части компьютера
- •2.11. Логические элементы
- •2.12. Триггеры
- •2.12.1. Общие сведения о триггерах
- •2.12.2. Асинхронный rs-триггер
- •2.12.3. Синхронный rs-триггер
- •2.12.3. Двухтактный rs-триггер
- •2.12.4. Асинхронный и синхронный d-триггеры
- •2.12.5. T-триггер
- •2.12.6. Jk-триггер
- •2.13. Типовые узлы комбинационного типа
- •2.13.1. Дешифраторы
- •2.13.2. Одноразрядный сумматор
- •2.13.3. Полусумматор
- •2.13.4. Многоразрядные сумматоры
- •2.13.5. Двоично-десятичные сумматоры
- •2.13.6. Мультиплексоры
- •2.13.7. Демультиплексоры
- •2.14. Типовые узлы накапливающего типа
- •2.14.1. Регистры
- •2.14.2. Счетчики
- •2.14.3. Двоично-десятичные счетчики
- •2.15. Классификация архитектур системы команд
- •2.15.1. Классификация по составу и сложности команд
- •2.15.2. Классификация по месту хранения операндов
- •2.15.3. Стековая архитектура
- •2.15.4. Аккумуляторная архитектура
- •2.15.5. Регистровая архитектура
- •2.15.6. Архитектура с выделенным доступом к памяти
- •2.16. Типы команд
- •2.16.1. Команды пересылки данных
- •2.16.2. Команды арифметической и логической обработки
- •2.16.3. Операции с целыми числами
- •2.16.4. Операции с числами в форме с плавающей запятой
- •2.16.5. Логические операции
- •2.16.6. Операции сдвигов
- •2.16.7. Операции с десятичными числами
- •2.16.8. Simd-команды
- •2.16.9. Команды для работы со строками
- •2.16.10. Команды преобразования
- •2.16.11. Команды ввода/вывода
- •2.16.12. Команды управления системой
- •2.16.13. Команды управления потоком команд
- •2.17. Формат команд
- •2.17.1. Длина команды
- •2.17.2. Разрядность полей команды
- •2.17.3. Выбор адресности команд
- •2.18. Способы адресации операндов
- •2.18.1. Непосредственная адресация
- •2.18.2. Прямая адресация
- •2.18.3. Косвенная адресация
- •2.18.4. Регистровая адресация
- •2.18.5. Косвенная регистровая адресация
- •2.18.6. Адресация со смещением
- •2.18.7. Относительная адресация
- •2.18.8. Базовая регистровая адресация
- •2.18.9. Индексная адресация
- •2.18.10. Страничная адресация
- •2.18.11. Блочная адресация
- •2.18.12. Распространенность различных видов адресации
- •2.19. Способы адресации в командах управления потоком команд
- •2.20. Функциональная организация фон-неймановской вычислительной машины
- •2.20.1. Устройство управления
- •2.20.2. Арифметико-логическое устройство
- •2.20.3. Основная память
- •2.20.4. Модуль ввода/вывода
- •2.21. Цикл команды
- •2.21.1. Стандартный цикл команды
- •2.21.2. Описание стандартных циклов команды для гипотетической машины
- •2.21.3. Машинный цикл с косвенной адресацией
2.13.6. Мультиплексоры
Мультиплексор представляет собой комбинационную схему с несколькими входами и одним выходом. Входы мультиплексора делятся на информационные и управляющие (адресные). Мультиплексор передает данные с одного из информационных входов на выход. Номер (адрес) подключаемого входа задается на управляющих входах. Мультиплексор с k управляющими входами может иметь до 2k информационных входов. Для выбора подключаемого входа используется дешифратор. Функциональная схема мультиплексора с двумя управляющими (A0 и A1) и четырьмя информационными (D0 ... D3) входами показаны на рис. 2.31, а. Схема мультиплексора включает в себя дешифратор на два входа и выходную схему. При поступлении адреса A1 A0 на входы дешифратора на одном из его выходов формируется сигнал «1», который подключает вход Di с заданным адресом к выходу схемы. Условное графическое обозначение мультиплексора приведено на рис. 3.24, б.

Рис. 2.31. Мультиплексор:
а – функциональная схема; б – условное графическое обозначение
Используя теорему разложения булевой функции, на мультиплексорах можно реализовать любую логическую функцию. Из мультиплексоров с небольшим числом входов можно построить мультиплексор с необходимым числом входов, используя каскадные схемы (рис. 2.32).
Схема (рис. 2.32, а) реализует таблицу истинности элемента И-НЕ на два входа, так как на входах схемы зафиксированы значения функции И-НЕ, а на адресные входы подаются значения переменных х и у. Для выполнения операции сложения переменных х, y и z по модулю 2 входные сигналы подаются так, как это показано на рис. 2.32, б. Если, например, х = 0, у = 1, z = 0, то на адресные входы поступит адрес «01», будет выбран вход 1, и на выход будет выдан сигнал F = z = 1, т.е. F = x у z = 0 1 0= 1. Если на вход схемы (рис. 2.32, в) подать комбинацию сигналов abcde = 00100, то cd = 10 и, следовательно, на мультиплексорах первого яруса будет выбран вход 2. При этом на вход 0 мультиплексора второго яруса поступит сигнал е, а на входы 1 и 2 – сигнал «0». Так как ab = 00, будет выбран нулевой вход этого мультиплексора. На выходе схемы возникнет сигнал е = 1, т.е. будет обнаружен код, содержащий одну единицу. Пример каскадного мультиплексора на 16 входов приведен на рис. 2.32, г.
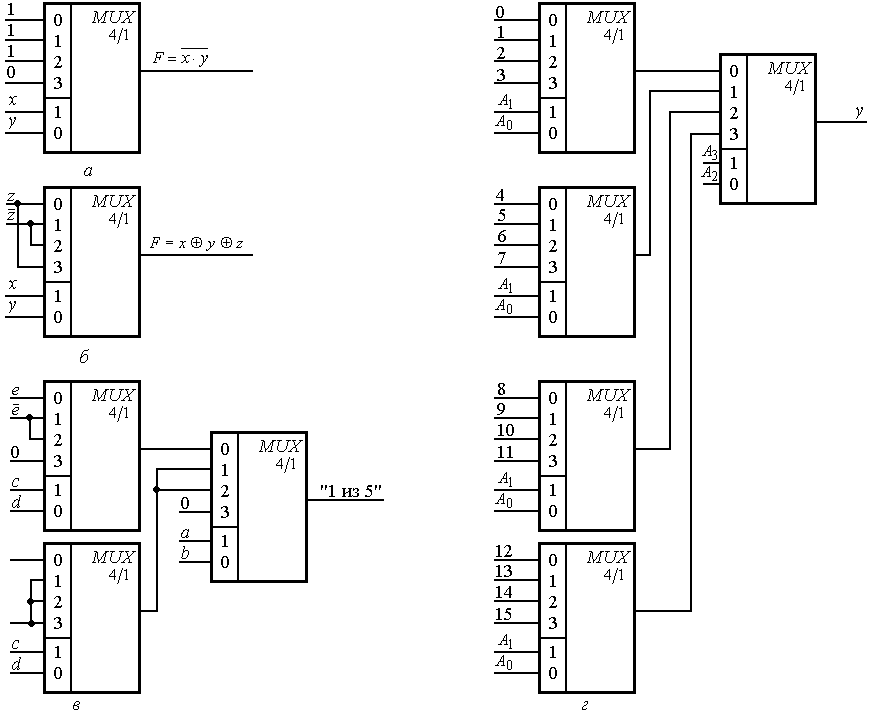
Рис. 2.32. Схемы реализации логических функций:
а – функция И-НЕ; б – сложение по модулю 2;
в – выделение наборов пяти переменных, содержащих единицу;
г – каскадный мультиплексор на 16 входов
2.13.7. Демультиплексоры
Демультиплексор – комбинационная схема с одним информационным входом, несколькими управляющими (адресными) входами и несколькими выходами. Демультиплексор передает сигнал с информационного входа на один из выходов, номер (адрес) которого задается сигналом на адресных входах. Таким образом, демультиплексор выполняет функцию, обратную по отношению к функции мультиплексора. Так как мультиплексор и демультиплексор выполняют функции, связанные с выбором одного из входов или выходов, их называют также селекторами. Максимальное число выходов демультиплексора составляет 2k, где k – число адресных входов. Функциональная схема демультиплексора с четырьмя информационными выходами и его условное графическое обозначение показаны на рис. 2.33. Входной сигнал D подается на входы всех выходных ключей, выполненных на элементах И. На вторые входы ключей поступают сигналы с выхода дешифратора, которые открывают один из ключей и разрешают входному сигналу пройти на выход схемы с заданными адресом.

Рис. 2.33. Демультиплексор:
а – функциональная схема; б – условное графическое обозначение
