
- •Раздел 2 принципы построения и функционирования эвм и вычислительных систем (вс)
- •2.1. Структура эвм
- •2.2. Системы счисления
- •2.3. Формы представления чисел
- •2.3.1. Форма представления чисел с фиксированной точкой
- •2.3.2. Форма представления чисел с плавающей точкой
- •2.3.3. Форматы двоично-десятичных чисел
- •2.3. Машинные коды
- •2.3.1. Прямой код
- •2.3.2. Обратный код
- •2.3.3. Дополнительный код
- •2.4. Перевод чисел из одной системы представления в другую
- •2.4.1. Перевод между основаниями, составляющими степень двойки
- •2.4.2. Перевод целого числа из десятичного счисления в другое
- •2.4.3. Перевод дробного числа из десятичного счисления в другое
- •2.4.4. Перевод чисел в десятичную систему счисления
- •2.5. Арифметические действия над двоичными числами
- •2.5.1. Сложение
- •2.5.2. Вычитание
- •2.5.3. Умножение
- •2.5.4. Деление
- •2.6. Понятие алгебры логики
- •2.7. Простейшие логические функции
- •2.7.1. Логическая операция конъюнкция (логическое умножение)
- •2.7.2. Логическая операция дизъюнкция (логическое сложение)
- •2.7.3. Логическая операция инверсия (отрицание)
- •2.7.4. Логическая операция сложение по модулю 2
- •2.7.5. Логическая операция эквивалентность (функция тождества)
- •2.7.6. Логическая операция импликация (логическое следование)
- •2.7.7. Функция Шеффера
- •2.7.8. Стрелка Пирса ав, или функция Вебба a b
- •2.8. Основные правила преобразования формул
- •2.9. Кодирование текстовой информации
- •2.10. Составные части компьютера
- •2.11. Логические элементы
- •2.12. Триггеры
- •2.12.1. Общие сведения о триггерах
- •2.12.2. Асинхронный rs-триггер
- •2.12.3. Синхронный rs-триггер
- •2.12.3. Двухтактный rs-триггер
- •2.12.4. Асинхронный и синхронный d-триггеры
- •2.12.5. T-триггер
- •2.12.6. Jk-триггер
- •2.13. Типовые узлы комбинационного типа
- •2.13.1. Дешифраторы
- •2.13.2. Одноразрядный сумматор
- •2.13.3. Полусумматор
- •2.13.4. Многоразрядные сумматоры
- •2.13.5. Двоично-десятичные сумматоры
- •2.13.6. Мультиплексоры
- •2.13.7. Демультиплексоры
- •2.14. Типовые узлы накапливающего типа
- •2.14.1. Регистры
- •2.14.2. Счетчики
- •2.14.3. Двоично-десятичные счетчики
- •2.15. Классификация архитектур системы команд
- •2.15.1. Классификация по составу и сложности команд
- •2.15.2. Классификация по месту хранения операндов
- •2.15.3. Стековая архитектура
- •2.15.4. Аккумуляторная архитектура
- •2.15.5. Регистровая архитектура
- •2.15.6. Архитектура с выделенным доступом к памяти
- •2.16. Типы команд
- •2.16.1. Команды пересылки данных
- •2.16.2. Команды арифметической и логической обработки
- •2.16.3. Операции с целыми числами
- •2.16.4. Операции с числами в форме с плавающей запятой
- •2.16.5. Логические операции
- •2.16.6. Операции сдвигов
- •2.16.7. Операции с десятичными числами
- •2.16.8. Simd-команды
- •2.16.9. Команды для работы со строками
- •2.16.10. Команды преобразования
- •2.16.11. Команды ввода/вывода
- •2.16.12. Команды управления системой
- •2.16.13. Команды управления потоком команд
- •2.17. Формат команд
- •2.17.1. Длина команды
- •2.17.2. Разрядность полей команды
- •2.17.3. Выбор адресности команд
- •2.18. Способы адресации операндов
- •2.18.1. Непосредственная адресация
- •2.18.2. Прямая адресация
- •2.18.3. Косвенная адресация
- •2.18.4. Регистровая адресация
- •2.18.5. Косвенная регистровая адресация
- •2.18.6. Адресация со смещением
- •2.18.7. Относительная адресация
- •2.18.8. Базовая регистровая адресация
- •2.18.9. Индексная адресация
- •2.18.10. Страничная адресация
- •2.18.11. Блочная адресация
- •2.18.12. Распространенность различных видов адресации
- •2.19. Способы адресации в командах управления потоком команд
- •2.20. Функциональная организация фон-неймановской вычислительной машины
- •2.20.1. Устройство управления
- •2.20.2. Арифметико-логическое устройство
- •2.20.3. Основная память
- •2.20.4. Модуль ввода/вывода
- •2.21. Цикл команды
- •2.21.1. Стандартный цикл команды
- •2.21.2. Описание стандартных циклов команды для гипотетической машины
- •2.21.3. Машинный цикл с косвенной адресацией
2.2. Системы счисления
В компьютере может храниться и обрабатываться информация различного характера: числа, адреса, команды, различные символы, графические изображения и т.д. Любая информация в компьютере представляется в числовой форме, при этом используются различные системы счисления.
Под системой счисления понимается способ представления чисел с помощью символов (цифр), имеющих определенное количественное значение. В любой системе счисления числа представляются в виде последовательности цифр.
В непозиционных системах счисления количественный эквивалент каждой цифры не зависит от ее положения в записи числа. Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления. В основе римской системы счисления лежат знаки I для числа 1, V для числа 5, X для 10, L для 50, а для обозначения чисел 100, 500 и 1000 стали применять первые буквы соответствующих латинских слов (Сentum – сто, Demimille – половина тысячи, Мille – тысяча).
Чтобы записать число его надо разложить на сумму тысяч, полутысяч, сотен, полусотен, десятков, пятков, единиц. Например, десятичное число 28 представляется следующим образом:
XXVIII = 10 + 10 + 5 + 1 + 1 + 1 (три десятка, пяток, три единицы).
В позиционных системах счисления количественное значение цифры зависит от ее места в числе. В позиционных системах счисления каждая цифра имеет вес. Обычно вес старшей цифры по отношению к весу соседней младшей цифры больше в количество раз, равное основанию системы счисления. При этом для целых чисел вес младшего разряда в любой системе счисления равен единице.
Основные достоинства любой позиционной системы счисления – простота выполнения арифметических операций и ограниченное количество цифр, необходимых для записи любых чисел. Примером позиционной системы счисления служит десятичная система счисления, которой мы широко пользуемся.
В позиционной системе счисления любое вещественное число в развернутой форме может быть представлено в следующем виде:

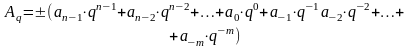
или
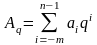 ,
,
здесь
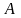 – само число,
– само число,
q – основание системы счисления,
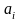 – цифры, принадлежащие алфавиту данной
системы счисления,
– цифры, принадлежащие алфавиту данной
системы счисления,
n – число целых разрядов числа,
m – число дробных разрядов числа.
Так десятичное число А10 = 4718,63 в развернутой форме запишется так:
А10 = 4 · 103 + 7 ·102 + 1 ·101 + 8 · 100 + 6 · 10-1 + 3 · 10-2
В современных компьютерах используются позиционные системы счисления с основаниями 2, 8, 10 и 16. В табл. 2.1 приведены возможные способы изображения первых 16 чисел во всех четырех системах счисления.
Двоичная система счисления.
Основание системы счисления q = 2.
Алфавит: 0, 1.
В этом случае формула принимает вид:
Таблица 2.1
Двоичные числа D2 |
Восьмеричные числа D8 |
Десятичные числа D10 |
Шестнадцатеричные числа D16 |
0000 |
0 |
0 |
0 |
0001 |
1 |
1 |
1 |
0010 |
2 |
2 |
2 |
0011 |
3 |
3 |
3 |
0100 |
4 |
4 |
4 |
0101 |
5 |
5 |
5 |
0110 |
6 |
6 |
6 |
0111 |
7 |
7 |
7 |
1000 |
10 |
8 |
8 |
1001 |
11 |
9 |
9 |
1010 |
12 |
10 |
А |
1011 |
13 |
11 |
В |
1100 |
14 |
12 |
С |
1101 |
15 |
13 |
D |
1110 |
16 |
14 |
Е |
1111 |
17 |
15 |
F |
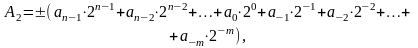
здесь – возможные цифры (0, 1).
Записав двоичное число А2 = 1001,1 в развернутом виде и произведя вычисления, получим это число, выраженное в десятичной системе счисления:
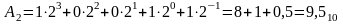
Восьмеричная система счисления.
Основание: q = 8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.
Записав восьмеричное число А8=7764,1 в развернутом виде и произведя вычисления, получим это число, выраженное в десятичной системе счисления:
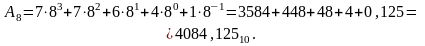
Шестнадцатеричная система счисления.
Основание: q = 16.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Здесь только десять цифр из шестнадцати имеют общепринятое обозначение 0,1, …9. Для записи остальных цифр (10, 11, 12, 13, 14 и 15) обычно используются первые пять букв латинского алфавита. Таким образом, запись 3АF16 означает:
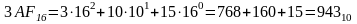 .
.
При хранении и обработке информации внутри компьютера используется двоичная система счисления. Это объясняется необходимостью физического представления только двух цифр (0 и 1), простотой выполнения арифметических операций и возможностью осуществления любых преобразований информации с помощью двоичных логических элементов.
Шестнадцатеричная (и реже восьмеричная) система счисления используется для более компактного представления информации (по сравнению с двоичной системой) при вводе и выводе больших массивов двоичных данных. Это связано с простотой перехода от двоичной системы счисления к шестнадцатеричной (восьмеричной) и наоборот.
