Учет массы упругой системы при колебаниях.
Если колеблющаяся система, несущая груз Q, обладает довольно значительной распределенной массой (число степеней свободы, следовательно, велико), то упрощенные расчеты, будут иметь уже значительную погрешность. В этом случае дифференциальные уравнения движения составляются с учетом массы системы. При решении подобного рода задач удобнее исходить не из условий равновесия, а из закона сохранения энергии.
Полагая, что количество энергии, сообщенное системе при выведении ее из положения равновесия и представляющее собой сумму кинетической и потенциальной энергии груза и упругой системы, при свободных колебаниях остается постоянным, получаем уравнение
|
|
(4) |
Это
уравнение показывает, что при колебаниях
происходит непрерывный процесс
преобразования энергии из одного вида
в другой, не сопровождающийся какими-либо
потерями энергии. Когда упругая система
достигает одного из крайних положений,
в котором скорость колебательного
движения равна нулю, а следовательно,
равна нулю и кинетическая энергия (T=0),
потенциальная энергия груза и системы
достигает наибольшего значения
;
наоборот, в положении равновесия
и
.
Заметим, что принцип, положенный в основу этого уравнения, применим лишь для систем с одной степенью свободы, так как закон сохранения энергии не учитывает обмена энергии, происходящего в системах с несколькими степенями свободы. Таким образом, решение задачи о колебаниях системы с большим числом степеней свободы здесь сводится к простейшей задаче и мы сможем приближенно найти лишь одну (первую) частоту свободных колебаний.
Рассмотрим теперь некоторые примеры использования исходного уравнения.
В
качестве первого примера исследуем
колебания груза Q,
подвешенного к нижнему концу призматического
стержня длиной l,
площадью поперечного сечения F
и удельным весом
(Рис.
4). Выведенный из положения равновесия
и затем предоставленный самому себе
груз начнет совершать продольные
колебания около положения равновесия.
Составим выражения для U
и Т
колеблющейся системы: груз — стержень.
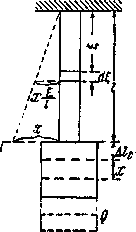Рис.4.
Расчетная схема колебаний подвешенного
груза
Потенциальная
энергия системы по сравнению с положением
равновесия изменится на
,
где
—
потенциальная энергия системы в начальный
момент (в положении равновесия), a
—
в момент t.
Потенциальную
энергию груза Q
в начальный момент обозначим через
;
потенциальная энергия стержня в тот же
момент равна
,
где
—
статическая деформация стержня от груза
Q.
Таким образом,
В
момент t,
когда груз переместится на расстояние
х
и стержень получит такую же дополнительную
деформацию х,
потенциальная энергия груза уменьшится
на Qx,
а сила упругого сопротивления стержня
и статическая деформация его увеличатся
в отношении
.
Поэтому
|
|
(5) |
Кинетическая
энергия системы складывается из
кинетической энергии груза
и
стержня
.
Кинетическая энергия груза
.
При вычислении кинетической энергии
стержня учтем, что в некоторый момент
t
скорость груза и нижнего конца стержня
равна х',
а верхнего — нулю. Скорости промежуточных
сечений будут иметь значения, заключающиеся
между этими двумя.
Предположим,
что при колебаниях перемещения всех
сечений стержня по отношению к
закрепленному концу меняются по тому
же закону, что и при статическом
растяжении, т. е. пропорционально
расстоянию от закрепленного сечения.
Таким образом, если нижнее сечение
стержня переместилось на величину х,
то сечение, отстоящее от места защемления
на
,
переместится на величину
,
скорость этого сечения будет равна
.
Живая сила элемента стержня длиной
,
отстоящего на
от
закрепленного конца, будет равна:
Кинетическая
энергия всего стержня будет равна сумме
величин
,
т.е.
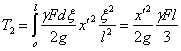
Таким
образом, живая сила стержня равна живой
силе груза, имеющего массу
,
т. е. равную трети массы стержня, и
двигающегося с той же скоростью х',
что и груз Q.
Полная же кинетическая энергия системы
груз — стержень будет:
Подставляя Т и выражение U (4) в уравнение (5), дифференцируем последнее по t и находим:
или
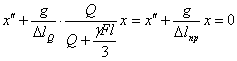
Здесь
—
статическая деформация от груза
.
Полученное дифференциальное уравнение
движения с учетом массы колеблющегося
стержня отличается от полученного ранее
уравнения только величиной множителя
при х
и полностью совпадает с ним, если
пренебречь массой стержня. Поэтому
поправка на массу стержня, которую нужно
ввести в предыдущие расчеты, состоит в
том, что при определении частоты свободных
колебаний стержня статическая деформация
его вычисляется не от груза Q,
но от груза Q,
сложенного с одной третью веса стержня.
Таким образом, учет массы колеблющегося
стержня уменьшает частоту свободных
колебаний и увеличивает их период.
Величину
называют
приведенной массой стержня.
Лекция № 49. Расчет динамического коэффициента при ударной нагрузке.