ЗАДАНИЕ. На вал АВ установлены два зубчатых колеса 1 и 2 диаметрами D1 и D2 соответственно, нагруженные усилиями от сопряжённых колёс.
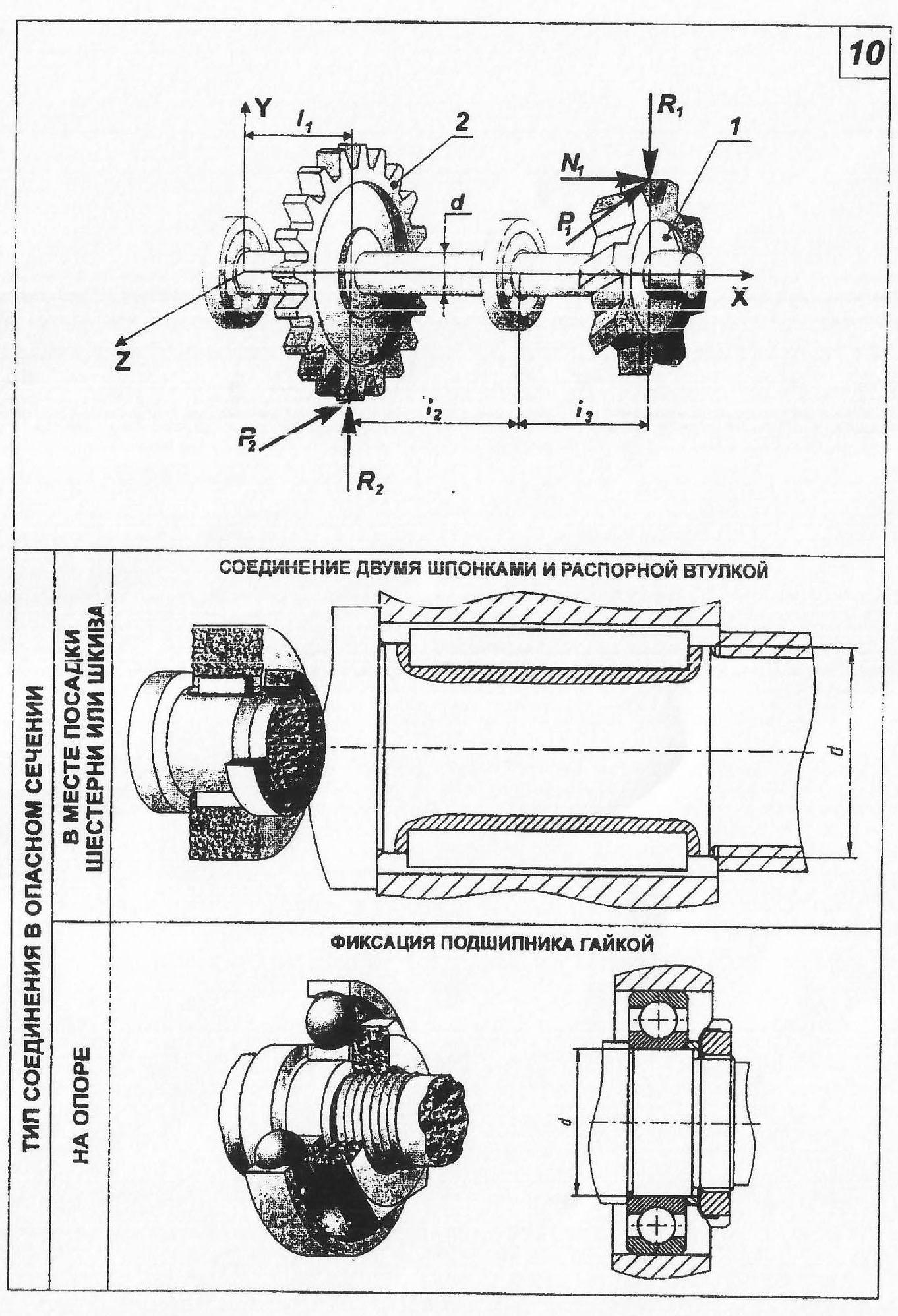
Необходимо:
подобрать диаметр вала d из условия статической прочности. В опасном сечении вала построить эпюры нормальных и касательных напряжений и показать напряжённое состояние тела в опасной точке;
произвести расчёт вала на жёсткость по линейным перемещениям в местах установки колёс и по угловым перемещениям в опорах. Уточнить диаметр вала;
выполнить проверочный расчёт вала на усталостную прочность в опасном сечении.
Исходные расчётные данные
|
N1, кН |
R1, кН |
Р1, кН |
l1, м |
l2, м |
l3, м |
D1, м |
D2, м |
Марка стали |
|
0,82 |
0,47 |
2,60 |
0,15 |
0,6 |
0,3 |
0,3 |
0,4 |
45 |
Содержание
1. Проектировочный расчёт вала на статическую прочность 3
11
2. Расчёт вала на жёсткость 11
Горизонтальная плоскость 14
2.3. Расчёт на изгибную жёсткость. Уточнение диаметра вала 15
3. Расчёт вала на усталостную прочность. 17
19
3.6. Расчёт коэффициента запаса усталостной прочности. Проверка прочности. 24
4.Расчет на прочность плоской статически неопределимой рамы. 25
1. Проектировочный расчёт вала на статическую прочность
1.1. Построение расчётной схемы вала
При расчёте на статическую прочность представим вал АD в виде балки на двух опорах. Одну из опор примем шарнирно-неподвижной (сечение С), другую, как наиболее близко расположенную к коническому колесу, — шарнирно-подвижной (сечение В).
Заменим действие установленных на вал колёс соответствующими нагрузками. Вектор радиальной силы R1 перенесём в центр тяжести сечения вала по линии её действия. Векторы окружных сил Р1 и Р2 — параллельно самим себе. При этом появятся два крутящих сосредоточенных момента:
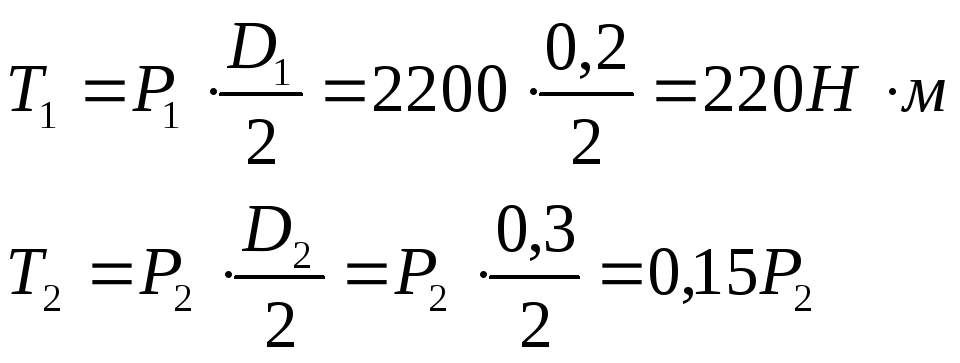
в сечениях А и D соответственно.
Для определения окружного усилия Р2 запишем уравнение статического равновесия в виде суммы моментов всех сил, действующих на вал, относительно продольной оси х:
откуда
Перенесём вектор силы N1 на ось вала. При этом в сечении А возникнет сосредоточенный изгибающий момент:
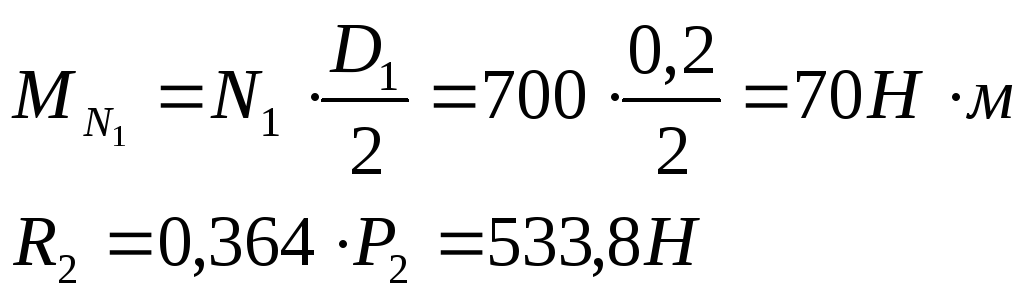
Силовые факторы, лежащие в вертикальной плоскости yx, вызовут в подшипниках реакции RBY и RCY, а в горизонтальной zx — RBZ и RCZ. Величины этих реакций определим, как для балки, лежащей на двух опорах.
1.2. Построение эпюр внутренних силовых факторов
Видно, что вал работает на совместное действие растяжения (сжатия), кручения и изгиба в вертикальной (yx) и горизонтальной (zx) плоскостях. Рассмотрим каждую деформацию отдельно, используя принцип независимости действия сил.
Определим опасную точку вала. Для этого установим, как меняются по длине вала внутренние силовые факторы, т.е. построим их эпюры.
Растяжение (сжатие)
Вал нагружен двумя сосредоточенными продольными силами: N1 и RCX = N1 в опоре С, которые вызывают на участке СD сжатие. Построим эпюру нормальных сил ЭN.
Кручение
Два скручивающих момента Т1 и Т2 вызывают кручение на участке АD. Эпюру крутящих моментов ЭТ строим также, как и при чистом кручении.
1.2.3. Изгиб в вертикальной плоскости yx
Эпюра ЭМZ изгибающих моментов относительно оси z строится от сил , R1 и R2 и изгибающего момента MN1, действующих в вертикальной плоскости. Из уравнений статического равновесия определим реакции в опорах В и С( RBY и RCY):
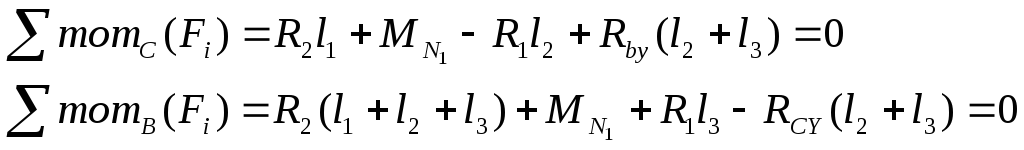
откуда
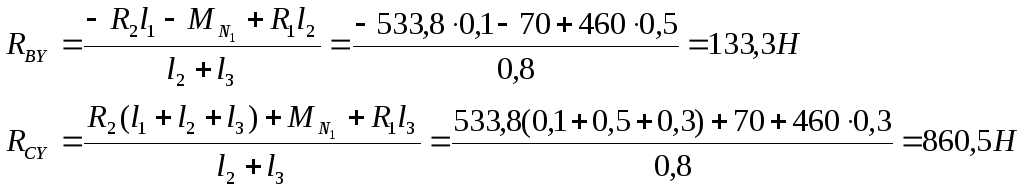
Проверим правильность определения реакций. Для этого запишем уравнения статического равновесия в виде суммы проекций всех сил Fi на ось y:
Следовательно, реакции RBY и RCY найдены верно.
1) Участок АВ
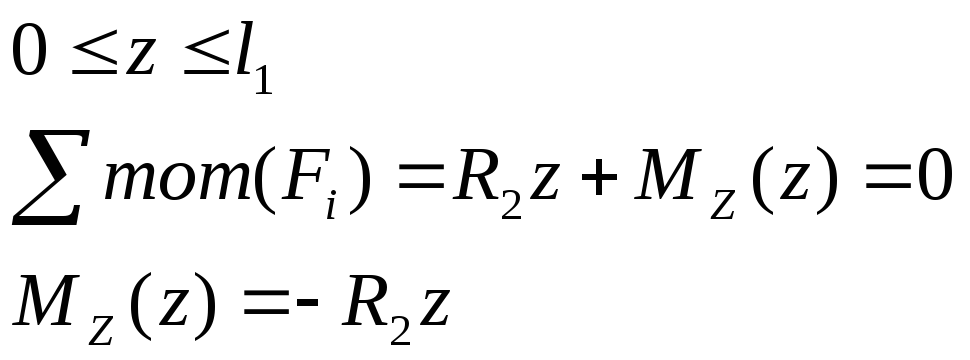
2) Участок ВС
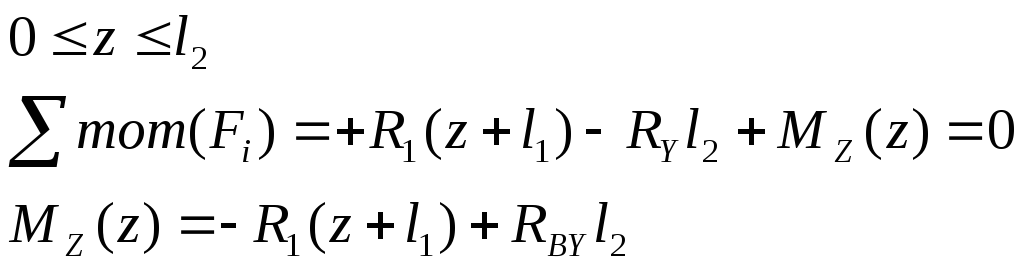
3) Участок СD
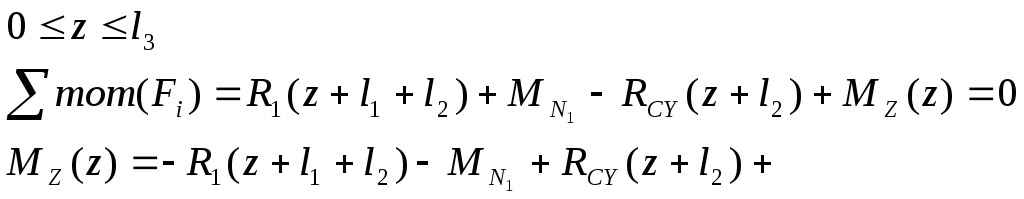
Вычислим изгибающие моменты МZ в сечениях А, В, С и D:
По полученным значениям строим эпюру ЭМZ.
1.2.4. Изгиб в горизонтальной плоскости zx
Эпюра ЭМY изгибающих моментов относительно оси у строится от сил Р1, Р2. Из уравнений статического равновесия определим реакции в опорах В и С (RBZ и RCZ):
откуда
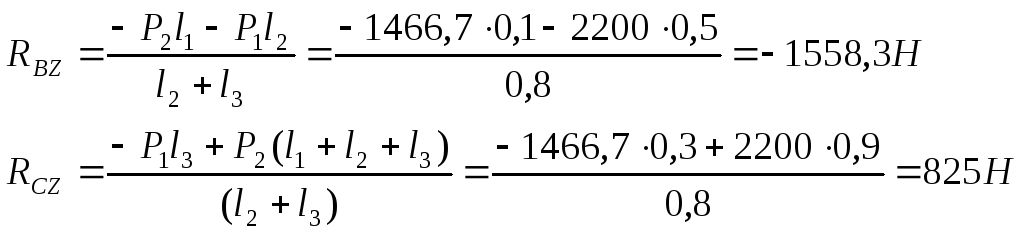
Проверим правильность определения реакций. Для этого запишем уравнения статического равновесия в виде суммы проекций всех сил Fi на ось z:
Следовательно, реакции RBZ и RCZ найдены верно.
1) Участок АВ
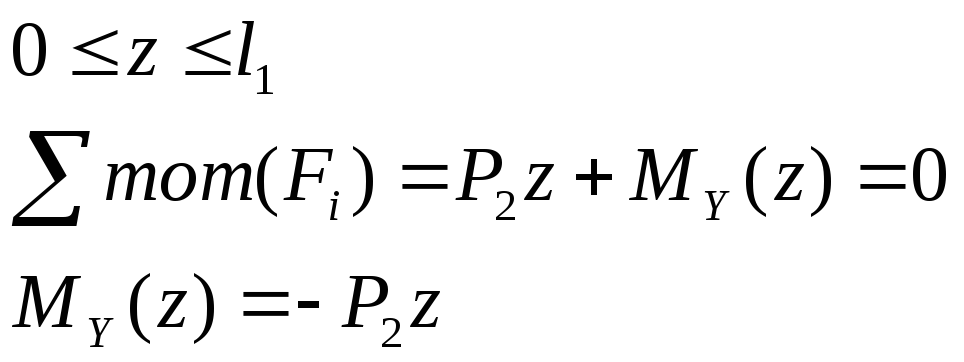
2) Участок ВС
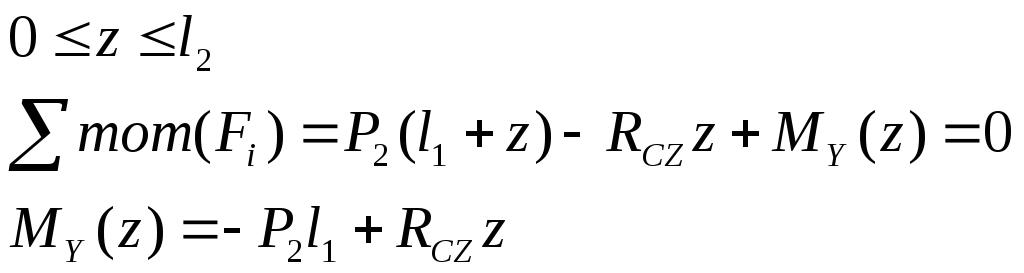
3) Участок СD
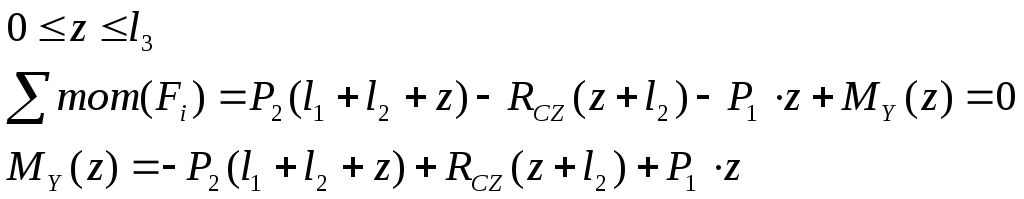
Вычислим изгибающие моменты МY в сечениях А, В, С и D:
По полученным значениям строим эпюру ЭМY.