Влияние резонанса на величину напряжений.

   Если на балке расположена машина с вращающимся грузом, имеющим эксцентриситет по отношению к оси вращения (Рис.1,). то

Рис.1. Расчетная схема неуравновешенного ротора машины

 

   Сила инерции груза будет вызывать в балке напряжения и деформации, периодически меняющие свой знак. Балка будет совершать колебания с периодом, равным периоду вращения груза. Это будут так называемые вынужденные колебания. Если период вынужденных колебаний совпадет с периодом свободных колебаний стержня, то мы получим явление резонанса, при котором амплитуда (размах) колебаний будет резко расти с течением времени. Наличие сил трения, сопротивление воздуха и т. д. ограничивают на практике рост этой амплитуды; однако она может достичь очень большой величины, значительно превышающей те деформации, которые испытывала бы конструкция под действием ускорений той же величины, но не меняющих знака.

   Известен случай, когда при резонансе угол закручивания вала увеличился в шесть раз по сравнению с тем углом, который был до наступления резонанса, — это был случай поломки коленчатых валов двигателей «Цеппелина» при первом его перелете через Атлантический океан.

   Таким образом, явление резонанса, если оно длится некоторое время, а не сбивается немедленно по возникновении, ведет к постепенному росту деформаций и пропорциональных им напряжений в конструкции, что может вызвать поломку. Поэтому, как правило, при проектировании конструкций, испытывающих переменные ускорения с постоянным периодом, необходимо избежать возникновения явления резонанса.

   Так как период раскачивающих (возмущающих) сил обычно является заданным, то в распоряжении проектировщика остается лишь период собственных свободных колебаний конструкции, который надо подобрать так, чтобы он в должной мере отличался от периода изменений возмущающей силы.

   Вопросы, связанные с определением периода, частоты и амплитуды свободных и вынужденных колебаний, рассматриваются в курсах теоретической механики. Поэтому ограничимся лишь приложением полученных там выводов к определению напряжений и проверке прочности элементов конструкции при колебаниях.

 

Вычисление напряжений при колебаниях.

   Упругая система, выведенная каким-либо путем из равновесия, приходит в колебательное движение. Колебания происходят около положения упругого равновесия, при котором в нагруженной системе имели место статические деформации и соответствующие им статические напряжения ( или — в зависимости от вида деформации). При колебаниях к статическим деформациям добавляются динамические, зависящие от вида колебательного движения и от величины размаха (амплитуды) колебаний. В связи с этим изменяются и напряжения . Таким образом, при расчете колеблющейся системы на прочность необходимо уметь вычислять динамические добавки к статическим деформациям и соответствующим им напряжениям.

   Во многих случаях характер колебаний системы может быть определен одной какой-нибудь величиной (одной координатой). Такие системы называются системами с одной степенью свободы; таковы, например, растянутая или сжатая незначительного веса пружина с грузом на конце, совершающая продольные колебания; небольшого (сравнительно с грузом Q) собственного веса балка, изображенная на Рис.2, колеблющаяся в направлении, перпендикулярном к ее оси, и т. п.

Рис.2. Динамическая модель колебаний системы с одной степенью свободы.

 

   При колебаниях систем с одною степенью свободы полные деформации системы в каком либо сечении могут быть найдены путем сложения статической деформации с добавочной деформацией при колебаниях. Для проверки прочности системы, очевидно, необходимо найти наиболее опасное сечение с наибольшей в процессе колебаний суммарной величиной деформации. В простейших случаях для этого потребуется сложить наибольшую статическую деформацию с наибольшей амплитудой колебаний А, т. е.

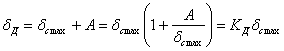
Пока система деформируется в пределах упругости, напряжения пропорциональны деформациям. Поэтому

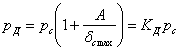
где

— коэффициент динамичности при колебаниях. Условие прочности в этом случае должно иметь такой вид:

   Таким образом задача нахождения динамических напряжений и проверки прочности при колебаниях может быть сведена к определению статических напряжений и коэффициента динамичности . Так как последний зависит от величины А, то нужно уметь определять наибольшее значение амплитуды колебаний в разных случаях.

   Как известно, дифференциальное уравнение движения колеблющегося груза Q в случае свободных колебаний можно представить в виде уравнения равновесия, в котором кроме внешней силы (веса груза Q) и силы упругого сопротивления системы учитывается также и сила инерции:

(1)

   Здесь х — координата, полностью определяющая положение груза Q во время колебаний; Р — полное упругое сопротивление системы при колебаниях; — так называемая восстанавливающая сила (добавочное упругое усилие, возникающее в системе в результате перемещения точки приложения груза Q на расстояние х при колебаниях), которую в пределах упругости можно считать пропорциональной координате х (); с — коэффициент пропорциональности, представляющий собой усилие, необходимое для того, чтобы вызвать равную единице статическую деформацию системы в направлении действия груза Q. Если статическая деформация от груза Q равна , то .

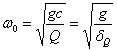   Решение уравнения (1) приводит к таким формулам для вычисления частоты и периода свободных колебаний:

и

   Свободные колебания невесомого тела суть простые гармонические колебания с частотой (периодом), равной частоте (периоду) колебаний математического маятника, длина которого равна статической деформации системы от груза Q. Так, например, если груз Q растягивает призматический стержень,

при изгибе балки на двух шарнирных опорах грузом Q посредине пролета

и т.д.

   Если на упругую систему, кроме груза Q и силы упругого сопротивления системы Р, в том же направлении действует периодически меняющаяся возмущающая сила S и сила сопротивления среды R, то дифференциальное уравнение движения груза Q при колебаниях также может быть представлено в виде уравнения равновесия, подобного уравнению (1):

(2)

   Силу сопротивления среды R на практике в довольно большом числе случаев можно считать пропорциональной первой степени скорости колебательного движения, т. е. . Если возмущающая сила S меняется по синусоидальному закону:

,

где , а — частота возмущающей силы, то уравнение (2) может быть переписано так:

или

(3)

   Здесь — так называемый коэффициент затухания колебаний,

a — найденная выше частота свободных колебаний системы, возникающих при отсутствии как возмущающей силы S так и силы сопротивления R.

   Решение уравнения (3) приводит к такому выражению для амплитуды А вынужденных колебаний при наличии сил сопротивления:

Здесь

— статическая деформация системы от наибольшей величины возмущающей силы S (). Отношение амплитуды вынужденных колебаний А к величине деформации называется коэффициентом нарастания колебаний :

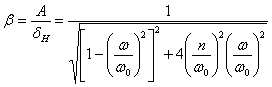
   Таким образом, формула (35.21) для динамического коэффициента получает теперь такой вид:

   В этом выражении не учтена амплитуда собственных колебаний системы, которая может иметь сколько-нибудь существенное значение лишь в самом начале процесса колебаний; при наличии сил сопротивления она довольно быстро уменьшается с течением времени.

   На рис.3 приведены графики изменения коэффициента нарастания колебаний в зависимости от величины отношения при разных значениях коэффициента затухания колебаний n ( отношения ). Если частота изменения возмущающей силы близка к частоте свободных колебаний системы, т. е. , и если величина коэффициента затухания колебаний сравнительно невелика, то знаменатели формул и для A и будут очень малыми, амплитуда колебаний и коэффициент нарастания колебаний будут очень большими. В этом случае даже небольшая возмущающая сила может вызвать высокие напряжения (явление резонанса).

Рис.3. Амплитудно-частотные характеристики системы.

 

   С увеличением сил сопротивления явление резонанса становится все менее заметным. Заметим, однако, что силы сопротивления значительно уменьшают величину амплитуды вынужденных колебаний только вблизи от резонанса при других величинах отношения — влияние сил сопротивления незначительно.

   Из рис. 3 видно, что если частота изменения возмущающей силы S очень мала, то амплитуда колебаний приближается к величине , коэффициент нарастания колебаний стремится к единице и наибольшие напряжения в системе могут быть вычислены как статические напряжения от груза Q и наибольшего значения возмущающей силы S.При очень большой частоте изменения возмущающей силы S амплитуда колебаний и коэффициент нарастания колебаний стремятся к нулю, груз Q можно рассматривать как неподвижный; поэтому наибольшее напряжение в системе равно статическому напряжению от груза Q.

   Это обстоятельство имеет очень большое практическое значение; оно используется при конструировании разного рода поглотителей колебаний, сейсмографов, вибрографов и других приборов. В машиностроении амортизаторы, предохраняющие основания машин от усилий, возникающих при колебаниях, подбираются так, чтобы частота собственных колебаний машины на амортизаторах была значительно меньше частоты изменения возмущающей силы.